A small block of wood of density 0.4×103kg/m3 is submerged in water at a depth of 2.9m. Find
(a) the acceletation of the block towards the surface when the block is released and
(b) the time for the block to reach the surface, Ignore viscosity.
The correct Answer is:A, B, C, D
To solve the problem step by step, we will address both parts of the question: (a) finding the acceleration of the block towards the surface when it is released, and (b) calculating the time for the block to reach the surface.
Part (a): Finding the Acceleration of the Block
1. Identify the Forces Acting on the Block:
- The weight of the block (W) acting downwards.
- The buoyant force (F_b) acting upwards.
2. Calculate the Weight of the Block:
- The weight of the block can be expressed as:
W=Density of the block×Volume of the block×g
- Let the density of the block be ρ=0.4×103kg/m3 and g≈9.8m/s2.
3. Calculate the Buoyant Force:
- The buoyant force can be expressed as:
Fb=Density of water×Volume of the block×g
- The density of water is approximately ρL=103kg/m3.
4. Set Up the Equation of Motion:
- The net force (F_net) acting on the block when it is released is given by:
Fnet=Fb−W
- Substituting the expressions for weight and buoyant force:
Fnet=(ρL⋅V⋅g)−(ρ⋅V⋅g)
- Factor out V⋅g:
Fnet=V⋅g⋅(ρL−ρ)
5. Calculate the Acceleration:
- Using Newton's second law, F=m⋅a, where m is the mass of the block:
a=Fnetm
- Since m=ρ⋅V, we can write:
a=V⋅g⋅(ρL−ρ)ρ⋅V=g⋅ρL−ρρ
- Substitute the values:
a=g⋅(103−0.4×103)0.4×103
a=g⋅600400=g⋅32
- Therefore, the acceleration is:
a=32g
- Substituting g≈9.8m/s2:
a≈32×9.8≈14.7m/s2
Part (b): Finding the Time to Reach the Surface
1. Use the Equation of Motion:
- The equation of motion for an object starting from rest is:
s=12at2
- Here, s=2.9m (the depth) and a=14.7m/s2.
2. Rearranging the Equation:
- Rearranging for t:
t2=2sa
t=√2sa
3. Substituting the Values:
- Substitute s=2.9m and a=14.7m/s2:
t=√2×2.914.7=√5.814.7≈√0.394≈0.63s
Final Answers:
- (a) The acceleration of the block towards the surface is approximately 14.7m/s2.
- (b) The time taken for the block to reach the surface is approximately 0.63s.
- The weight of the block (W) acting downwards.
- The buoyant force (F_b) acting upwards.
- The weight of the block can be expressed as:
W=Density of the block×Volume of the block×g
- Let the density of the block be ρ=0.4×103kg/m3 and g≈9.8m/s2.
- The buoyant force can be expressed as:
Fb=Density of water×Volume of the block×g
- The density of water is approximately ρL=103kg/m3.
- The net force (F_net) acting on the block when it is released is given by:
Fnet=Fb−W
- Substituting the expressions for weight and buoyant force:
Fnet=(ρL⋅V⋅g)−(ρ⋅V⋅g)
- Factor out V⋅g:
Fnet=V⋅g⋅(ρL−ρ)
- Using Newton's second law, F=m⋅a, where m is the mass of the block:
a=Fnetm
- Since m=ρ⋅V, we can write:
a=V⋅g⋅(ρL−ρ)ρ⋅V=g⋅ρL−ρρ
- Substitute the values:
a=g⋅(103−0.4×103)0.4×103
a=g⋅600400=g⋅32
- Therefore, the acceleration is:
a=32g
- Substituting g≈9.8m/s2:
a≈32×9.8≈14.7m/s2
- The equation of motion for an object starting from rest is:
s=12at2
- Here, s=2.9m (the depth) and a=14.7m/s2.
- Rearranging for t:
t2=2sa
t=√2sa
- Substitute s=2.9m and a=14.7m/s2:
t=√2×2.914.7=√5.814.7≈√0.394≈0.63s
- (a) The acceleration of the block towards the surface is approximately 14.7m/s2.
- (b) The time taken for the block to reach the surface is approximately 0.63s.
Topper's Solved these Questions
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.4
4 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.5
3 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Exercise16.2
2 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A small block of wood of relative density 0.5 is submerged in water. When the block is released, it stats moving upwards, the acceleration of the block is (g=10ms−2)
View SolutionA small block of wood of specific gravity 0.5 is subnerged at a depth of 1.2 m in a vessel filled with water. The vessel is accelerated upwards with an acceleration a0=g2. Time taken by the block to reach the surface, if it is released with zero initial velocity is (g=10m/s2)
View Solution
Knowledge Check
A block of wood of density 0.8gcm−3 has a volume of 60cm3 . The mass of block will be :
A60.8 gB75gC48gD0.013 g
A block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View SolutionFigure shows a block of mass 2m sliding on a block of mass m. Find the acceleration of each block . ( All surface are smoth )
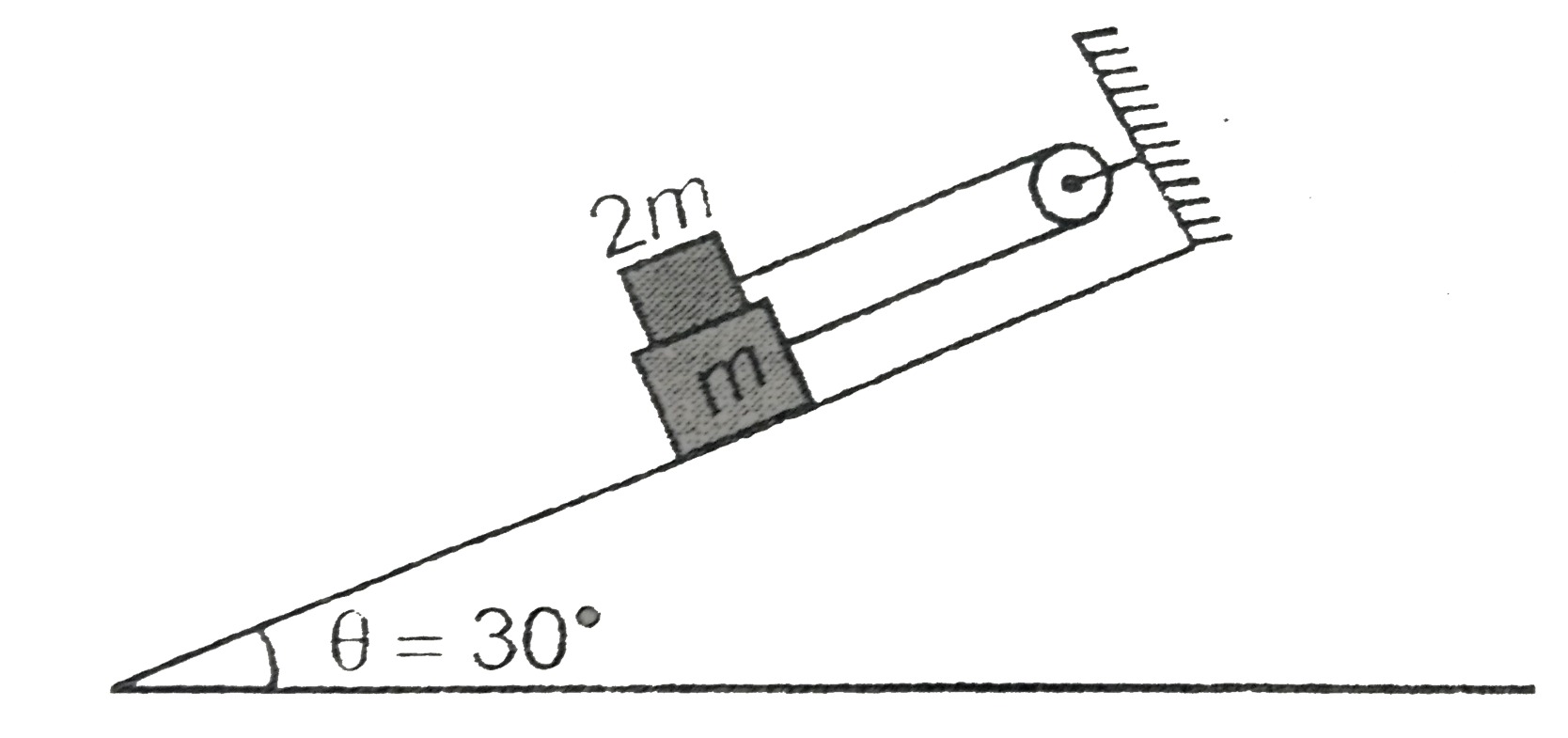
View SolutionA block of material of specific gravity 0.4 is held submerged at a depth of 1m in a vessel filled with water. The vessel is accelerated upwards with acceleration of ao=g/5. If the block is released at t = 0, neglecting viscous effects, it will reach the water surface at t equal to (g=10ms2) :
View SolutionA smooth wedge of mass M is pulled towards left with an acceleration a=gcotθ on a horizontal surface and a block of mass m is released w.r.t. wedge. Then answer the following

Time taken by the block to reach the ground is
View SolutionA block of wood of density 500kg/m3 has mass m kg in air. A lead block which has apparent weight of 28kg in water is attached to the block of wood, and both of them are submerged in water. If their combined apparent weight in water is 20kg, find the value of m. Take density of water =1000kg/m3
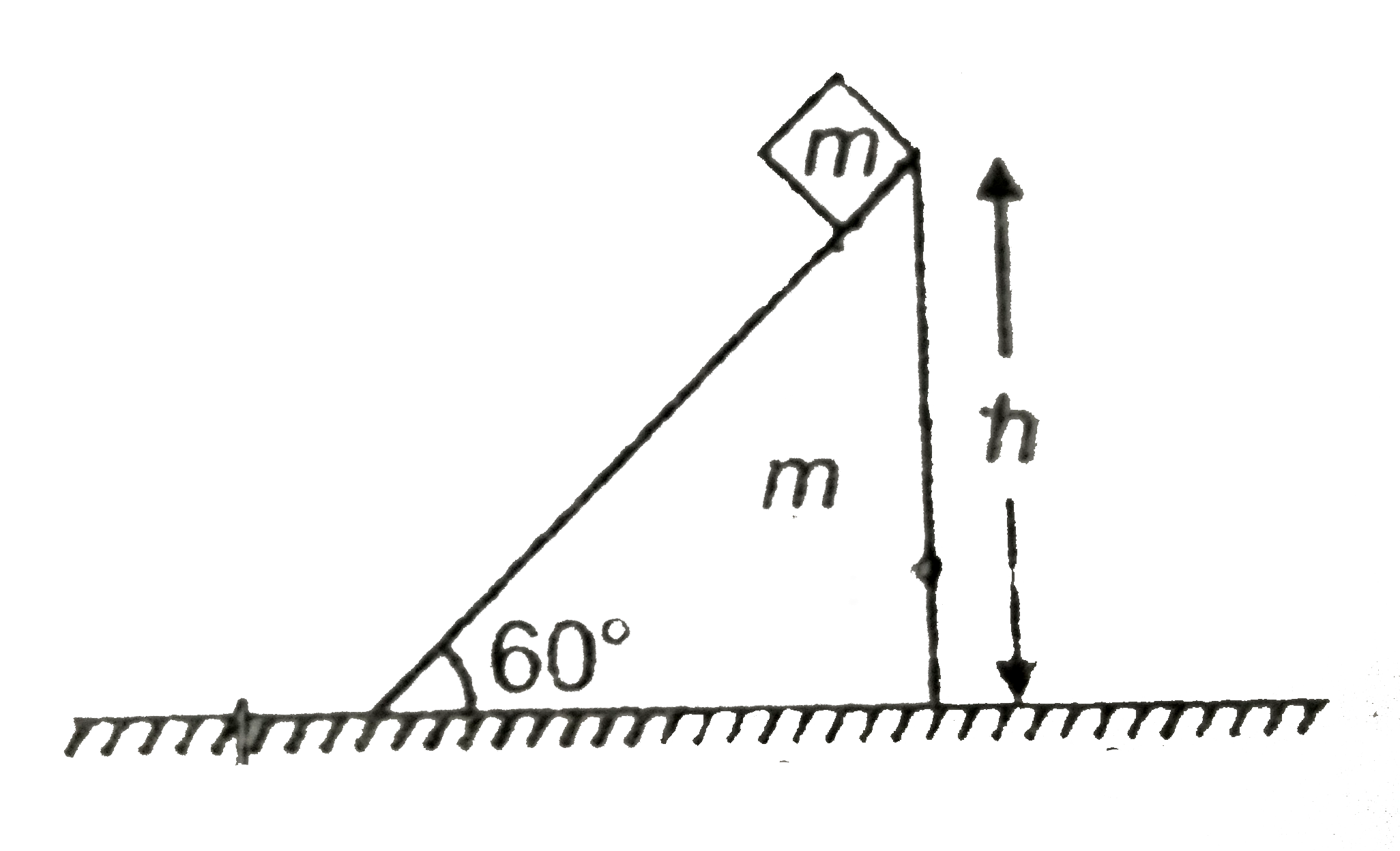
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View SolutionA block of wood of mass 24 kg floats on water. The volume of wood is 0.032m3 Find
a.the volume of block below the surface of water,
b.the density of wood.
(Denstiy of water =1000kgm−3)
View Solution
