A block of material of specific gravity 0.4 is held submerged at a depth of 1m in a vessel filled with water. The vessel is accelerated upwards with acceleration of ao=g/5. If the block is released at t = 0, neglecting viscous effects, it will reach the water surface at t equal to (g=10ms2) :
0.6 sec
0.33 sec
1.2 sec
1 sec
The correct Answer is:B
To solve the problem step by step, we will analyze the forces acting on the block and calculate the time taken for the block to reach the water surface after being released.
Step 1: Understand the Given Information
- Specific gravity of the block (SG) = 0.4
- Depth of the block in water (h) = 1 m
- Acceleration of the vessel (a₀) = g/5, where g = 10 m/s²
- Therefore, a₀ = 10/5 = 2 m/s²
Step 2: Calculate the Effective Acceleration
When the vessel is accelerated upwards, the effective gravitational acceleration (g_net) acting on the block is the sum of the gravitational acceleration (g) and the pseudo force due to the upward acceleration of the vessel.
g_{net} = g + a₀ = g + \frac{g}{5} = g + 2 = 10 + 2 = 12 \text{ m/s²}
Step 3: Calculate the Density of the Block
The specific gravity (SG) is defined as the ratio of the density of the block (ρ_b) to the density of water (ρ_w).
SG=ρbρw
Given that SG = 0.4, we can express the density of the block as:
ρb=0.4⋅ρw
Step 4: Calculate the Buoyant Force and Weight
The buoyant force (F_b) acting on the block is given by Archimedes' principle:
Fb=ρw⋅V⋅gnet
The weight (W) of the block is:
W=ρb⋅V⋅g
Step 5: Set Up the Equation of Motion
The net force (F_net) acting on the block when it is released is the difference between the buoyant force and the weight of the block:
Fnet=Fb−W=ρw⋅V⋅gnet−ρb⋅V⋅g
Substituting the expression for ρ_b:
Fnet=ρw⋅V⋅gnet−(0.4⋅ρw)⋅V⋅g
Factoring out common terms:
Fnet=V⋅ρw(gnet−0.4g)
Step 6: Calculate the Acceleration of the Block
The mass of the block can be expressed as:
m=ρb⋅V=(0.4⋅ρw)⋅V
Using Newton's second law (F = ma), we can find the acceleration (a) of the block:
a=Fnetm=V⋅ρw(gnet−0.4g)(0.4⋅ρw)⋅V
The volume (V) cancels out:
a=gnet−0.4g0.4
Substituting the values of g and g_net:
a=12−0.4⋅100.4=12−40.4=80.4=20 m/s²
Step 7: Use the Equation of Motion to Find Time
Using the equation of motion h=ut+12at2, where initial velocity (u) = 0:
1=0+12⋅20⋅t2
Solving for t:
1=10t2⟹t2=110⟹t=√110=1√10≈0.316 seconds
Final Answer
The time taken for the block to reach the water surface is approximately 0.316 seconds.
---
- Specific gravity of the block (SG) = 0.4
- Depth of the block in water (h) = 1 m
- Acceleration of the vessel (a₀) = g/5, where g = 10 m/s²
- Therefore, a₀ = 10/5 = 2 m/s²
When the vessel is accelerated upwards, the effective gravitational acceleration (g_net) acting on the block is the sum of the gravitational acceleration (g) and the pseudo force due to the upward acceleration of the vessel.
g_{net} = g + a₀ = g + \frac{g}{5} = g + 2 = 10 + 2 = 12 \text{ m/s²}
The specific gravity (SG) is defined as the ratio of the density of the block (ρ_b) to the density of water (ρ_w).
Given that SG = 0.4, we can express the density of the block as:
ρb=0.4⋅ρw
The buoyant force (F_b) acting on the block is given by Archimedes' principle:
The net force (F_net) acting on the block when it is released is the difference between the buoyant force and the weight of the block:
The mass of the block can be expressed as:
Using the equation of motion h=ut+12at2, where initial velocity (u) = 0:
The time taken for the block to reach the water surface is approximately 0.316 seconds.
Topper's Solved these Questions
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE MAIN (LEVEL - 1 )
31 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - LEVEL -1
90 Videos
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
Similar Questions
A small block of wood of specific gravity 0.5 is subnerged at a depth of 1.2 m in a vessel filled with water. The vessel is accelerated upwards with an acceleration a0=g2. Time taken by the block to reach the surface, if it is released with zero initial velocity is (g=10m/s2)
View SolutionA cubical block of density ρ is floating on the surface of water. Out of its height L, fraction x is submerged in water. The vessel is in an elevator accelerating upward with acceleration a. What is the fraction immersed ?
View SolutionA block of mass m is suspended by a light thread from an elevator. The elevator is accelerating upward with uniform acceleration a. The work done by tension on the block during t seconds is (u = 0)
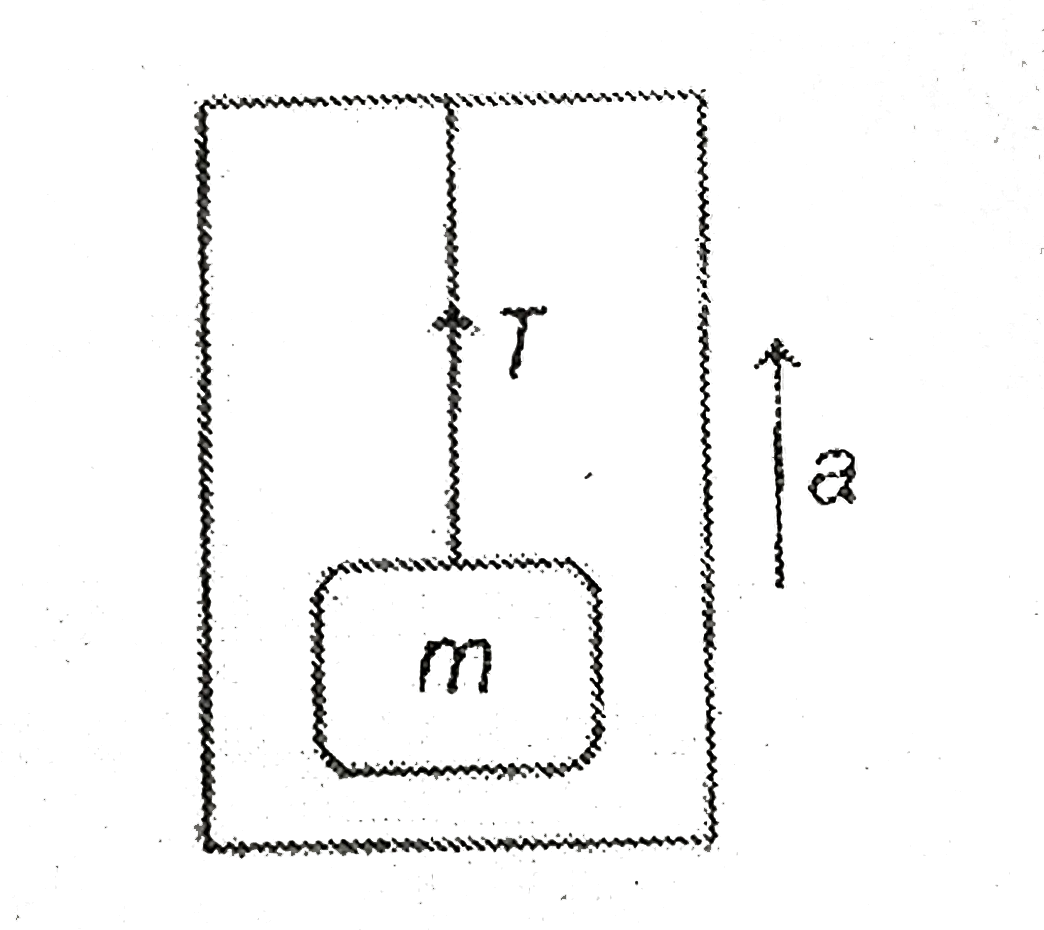
View SolutionA small block of wood of relative density 0.5 is submerged in water. When the block is released, it stats moving upwards, the acceleration of the block is (g=10ms−2)
View SolutionA block of mass 1 kg and density 0.8g/cm3 is held stationary with the help of a string as shown in figure. The tank is accelerating vertically upwards with an acceleration a =1.0m/s2. Find

(a) the tension in the string,
(b) if the string is now cut find the acceleration of block.
(Take g=10m/s2 and density of water =103kg/m3).
View SolutionFind the acceleration of the two blocks shown in figure-2.101.Take g=10m/s2
View SolutionA small block of wood of density 0.4×103kg/m3 is submerged in water at a depth of 2.9m. Find
(a) the acceletation of the block towards the surface when the block is released and
(b) the time for the block to reach the surface, Ignore viscosity.
View SolutionA wooden block is floating on water kept in a beaker. 40% of the block is above the water surface. Now the beaker is kept inside a lift that starts going upward with acceleration equal to g/2. The block will then
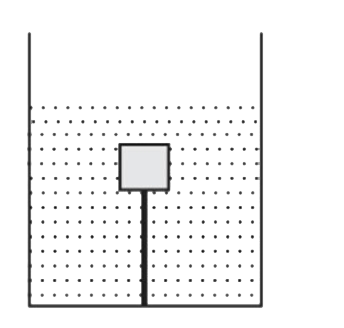
View SolutionA wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
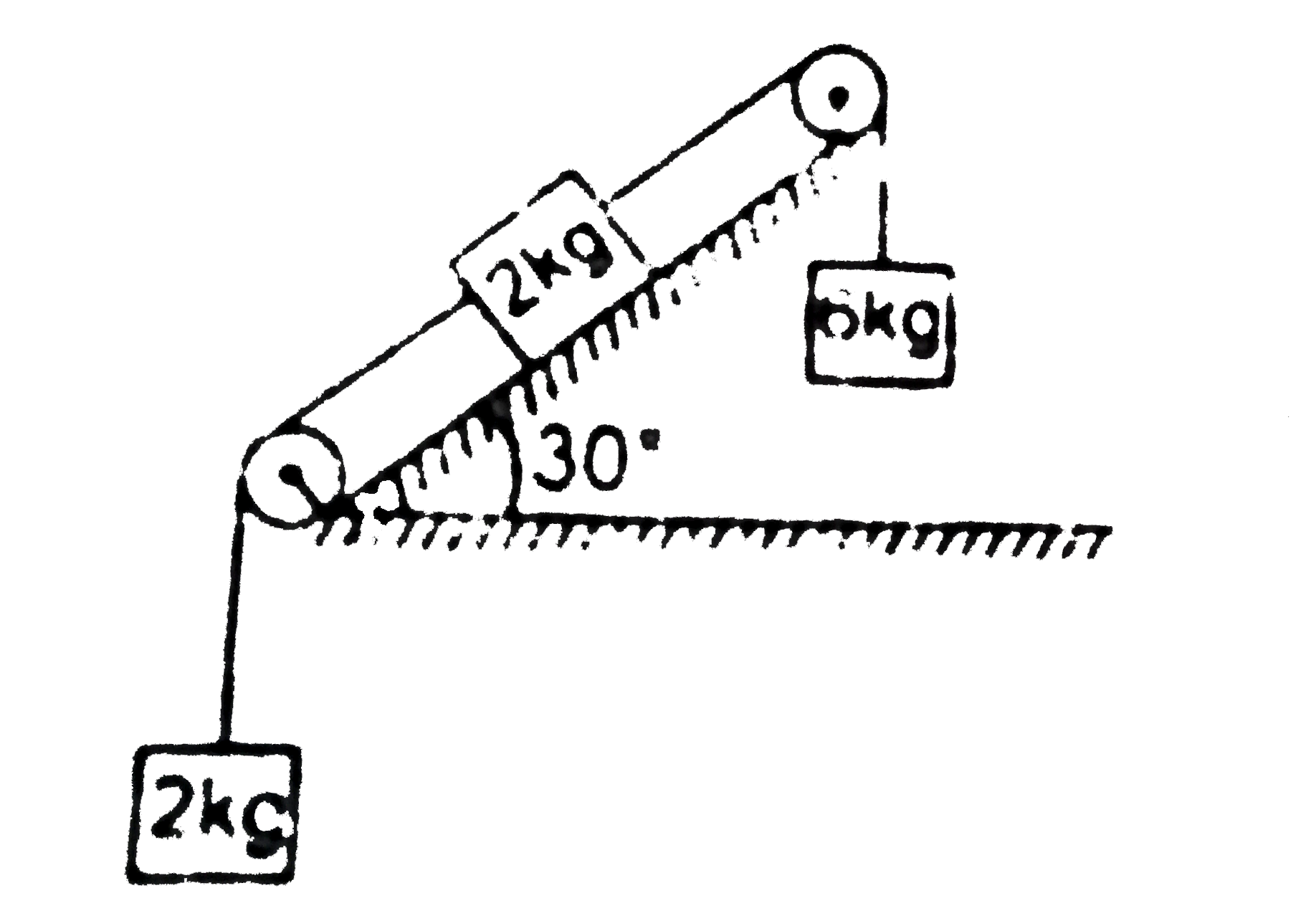
View SolutionFind the acceleration of the 6 kg block in the figure. All the surfaces and pulleys are smooth. Also the strings are inextensible and light. [Take g=10m/s2]
 .
.
View Solution
