Question

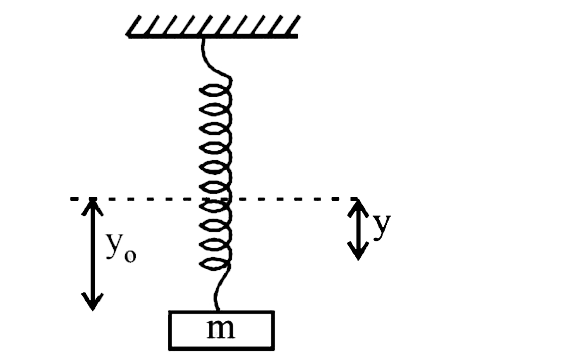
A small body attached to one end of a vertically hanging spring is performing (SHM) about is mean position with angular frequency (omega) and amplitude (a). If at a height (y*) from the mean position, the body gets detached from the spring, calculate the value of (y*) so that the height (H) attained by the mass is maximum. The body does noy interact with the spring during its subsquent motion after detachment. $(a{\omega }^2>g)$.
.

Answer

A::B

Explanation

If a small mass is attached to ane end of a vertically haning spring then it performs SHM.
Angular frequency=omega, Amplitude=alpha`
Under SHM, velocity `v=omegasqrta^(2)-y^(2)`
After detaching from spring, net downward acceleration of the block `=g.
:. Height attained by the block`=h`
:. `h=y+v^(2)/2_(g) or `h=y+(omega^(2)(a^(2)-y^(2)))/2_(g)`
For (h) to be maximum,(dh)/(dy)=o,y=y*`.
:. (dh)/(dy)=1+omega^(2)/2_(g)(-2y*) or 0=1-(2omega^(2)y*)/2_(g)`
or `(omega^(2)y*)/g=1 or y*=g/omega^(2)`
or `(omega^(2)y*)/8=1 or y*=g/omega^(2)`
Since a omega^(2)gtg(given)`
:. `agtg/omega^(2):.agty*.y* from mean position lta.
Hence `y*=g/omega^(2)`.