A small conducting sphere of radius r is lying concentrically inside a bigger hollow conducting sphere of radius R. The bigger and smaller spheres are charged with Q and q(Q>q) and are insulated from each other. The potential difference between the spheres will be
14πε0(qr−QR)
14πε0(QR+qr)
14πε0(qr−rR)
14πε0(qR−Qr)
The correct Answer is:C
To find the potential difference between the small conducting sphere and the larger hollow conducting sphere, we can follow these steps:
Step 1: Understand the System
We have two concentric conducting spheres:
- A smaller conducting sphere of radius r with charge q.
- A larger hollow conducting sphere of radius R with charge Q.
Step 2: Identify the Points of Interest
Let's denote:
- Point A: the surface of the smaller sphere (radius r).
- Point B: the inner surface of the larger sphere (radius R).
Step 3: Calculate the Potential at Point A (VA)
The potential VA at the surface of the smaller sphere due to its own charge q is given by the formula:
VA=14πϵ0⋅qr
Step 4: Calculate the Potential at Point B (VB)
The potential VB at the inner surface of the larger sphere due to its charge Q is given by:
VB=14πϵ0⋅QR
Step 5: Calculate the Total Potential at Point A (VA)
Since the potential due to the larger sphere does not affect the potential at the surface of the smaller sphere (as the electric field inside a conductor is zero), we can write:
VA=14πϵ0(qr+QR)
Step 6: Calculate the Total Potential at Point B (VB)
The potential at point B due to the charge Q from the larger sphere is:
VB=14πϵ0⋅QR
Step 7: Find the Potential Difference (VA - VB)
Now, we can find the potential difference between the two points:
VA−VB=(14πϵ0(qr+QR))−(14πϵ0⋅QR)
This simplifies to:
VA−VB=14πϵ0(qr)
Final Result
Thus, the potential difference between the smaller sphere and the larger sphere is:
VA−VB=q4πϵ0r
We have two concentric conducting spheres:
- A smaller conducting sphere of radius r with charge q.
- A larger hollow conducting sphere of radius R with charge Q.
Let's denote:
- Point A: the surface of the smaller sphere (radius r).
- Point B: the inner surface of the larger sphere (radius R).
The potential VA at the surface of the smaller sphere due to its own charge q is given by the formula:
VA=14πϵ0⋅qr
The potential VB at the inner surface of the larger sphere due to its charge Q is given by:
VB=14πϵ0⋅QR
Since the potential due to the larger sphere does not affect the potential at the surface of the smaller sphere (as the electric field inside a conductor is zero), we can write:
VA=14πϵ0(qr+QR)
The potential at point B due to the charge Q from the larger sphere is:
VB=14πϵ0⋅QR
Now, we can find the potential difference between the two points:
VA−VB=(14πϵ0(qr+QR))−(14πϵ0⋅QR)
VA−VB=14πϵ0(qr)
Thus, the potential difference between the smaller sphere and the larger sphere is:
VA−VB=q4πϵ0r
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
A conducting sphere of radius r has a charge . Then .
View SolutionA conducting sphere of radius R, carrying charge Q, lies inside uncharged conducting shell of radius 2R. If they are joined by a metal wire,
View SolutionA common test to find the genotype of a hybrid is by
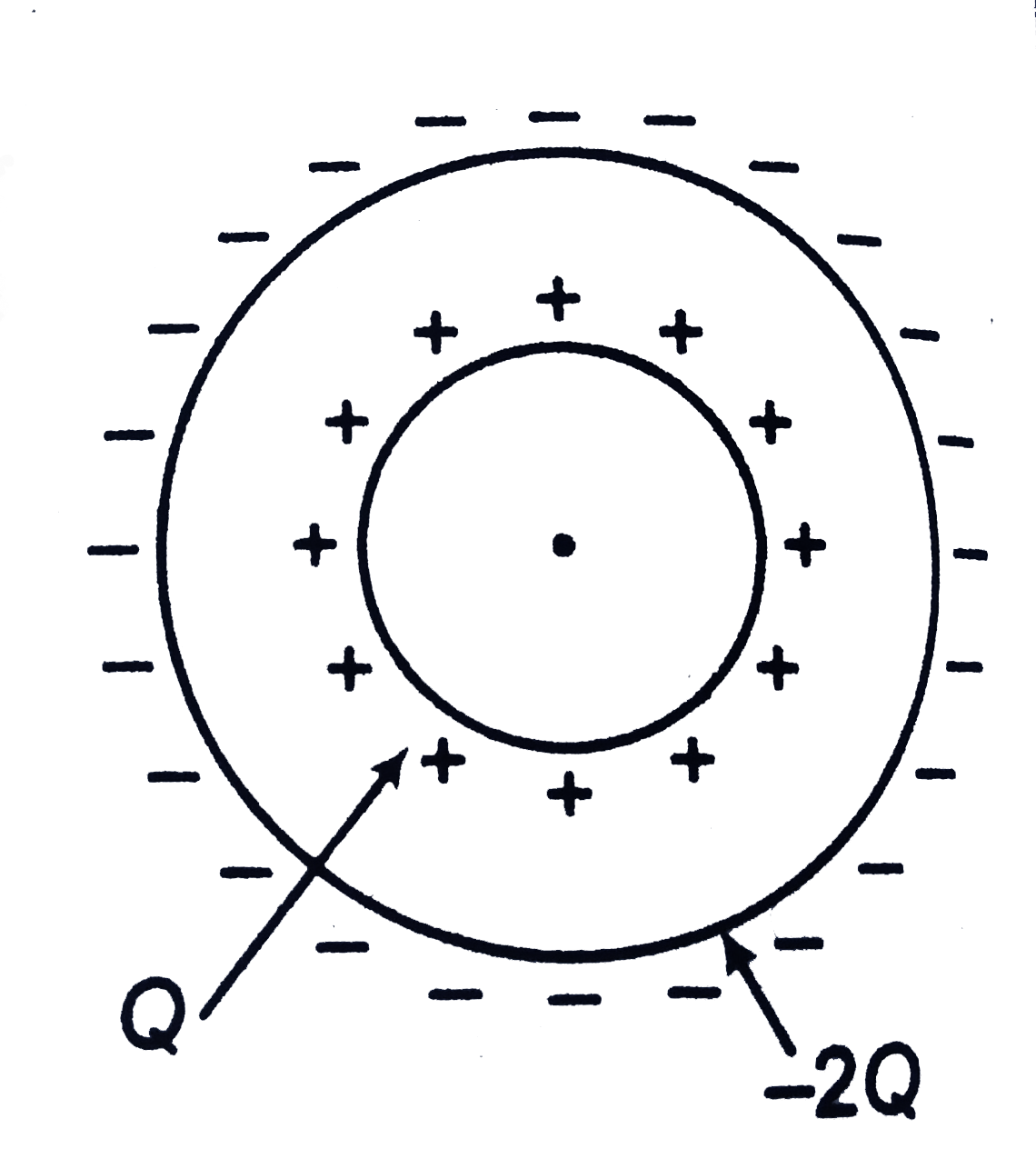
View SolutionTwo concentric conducting spheres of radii R and 2R are crrying charges Q and −2Q, respectively. If the charge on inner sphere is doubled, the potetial differece between the two spheres will
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionA hollow sphere of radius 2R is charged to V volts and another smaller sphere of radius R is charged to V/2 volts. Then the smaller sphere is placed inside the bigger sphere without changing the net charge on each sphere. The potential difference between the two spheres would becomes V/n. find value of n
View SolutionA hollow sphere of radius 2R is charged to V volts and another smaller sphere of radius R is charged to V/2 volts. Now the smaller sphere is placed inside the bigger sphere without changing the net charge on each sphere. The potential difference between the two spheres would be
View SolutionA hollow conducting sphere of inner radius r and outer radius 2R is given charge Q as shown in figure, then the

View SolutionA solid conducting sphere of radius r is having a charge of Q and point charge q is a distance d from the centre of sphere as shown. The electric potential at the centre of the solid sphere is :

View SolutionSelf energy of conducting sphere of radius .r. carrying charge .Q. is ______
View Solution
