Three identical charges are placed at corners of a equilateral triangel of side l. If force between any two charges is F, the work required to double the dimensiions of triangle is
−3Fl
3Fl
(−32)Fl
(32)Fl
The correct Answer is:C
To solve the problem of finding the work required to double the dimensions of an equilateral triangle with identical charges at its corners, we will follow these steps:
Step 1: Understand the Initial Setup
We have three identical charges Q placed at the corners of an equilateral triangle with side length l. The force F between any two charges can be expressed using Coulomb's law:
F=kQ2l2
where k is Coulomb's constant.
Step 2: Calculate the Initial Potential Energy
The potential energy U of the system of three charges can be calculated by considering the potential energy contributions from each pair of charges. There are three pairs of charges (1-2, 2-3, and 3-1):
U=U12+U23+U31=3⋅kQ2l
Thus, the initial potential energy is:
Uinitial=3⋅kQ2l
Step 3: Determine the Final Setup After Doubling the Dimensions
When the dimensions of the triangle are doubled, the new side length becomes 2l. The force between any two charges at this new distance is:
F′=kQ2(2l)2=kQ24l2
The potential energy of the system with the new side length is:
Ufinal=3⋅kQ22l=3kQ22l
Step 4: Calculate the Work Done
The work done W by an external agent to change the configuration of the charges is equal to the change in potential energy:
W=Ufinal−Uinitial
Substituting the values we calculated:
W=3kQ22l−3⋅kQ2l
This simplifies to:
W=3kQ22l−6kQ22l=−3kQ22l
Step 5: Substitute kQ2 in Terms of F
From the expression for force F=kQ2l2, we can express kQ2 as:
kQ2=Fl2
Substituting this into the work done expression:
W=−3(Fl2)2l=−3Fl2
Final Answer
Thus, the work required to double the dimensions of the triangle is:
W=−3Fl2
We have three identical charges Q placed at the corners of an equilateral triangle with side length l. The force F between any two charges can be expressed using Coulomb's law:
F=kQ2l2
where k is Coulomb's constant.
The potential energy U of the system of three charges can be calculated by considering the potential energy contributions from each pair of charges. There are three pairs of charges (1-2, 2-3, and 3-1):
U=U12+U23+U31=3⋅kQ2l
Thus, the initial potential energy is:
Uinitial=3⋅kQ2l
When the dimensions of the triangle are doubled, the new side length becomes 2l. The force between any two charges at this new distance is:
F′=kQ2(2l)2=kQ24l2
The potential energy of the system with the new side length is:
Ufinal=3⋅kQ22l=3kQ22l
The work done W by an external agent to change the configuration of the charges is equal to the change in potential energy:
W=Ufinal−Uinitial
Substituting the values we calculated:
W=3kQ22l−3⋅kQ2l
This simplifies to:
W=3kQ22l−6kQ22l=−3kQ22l
From the expression for force F=kQ2l2, we can express kQ2 as:
kQ2=Fl2
Substituting this into the work done expression:
W=−3(Fl2)2l=−3Fl2
Thus, the work required to double the dimensions of the triangle is:
W=−3Fl2
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (B) Chapter exercises
17 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - Check point 2.5
20 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Medical entrances gallery
37 Videos
Similar Questions
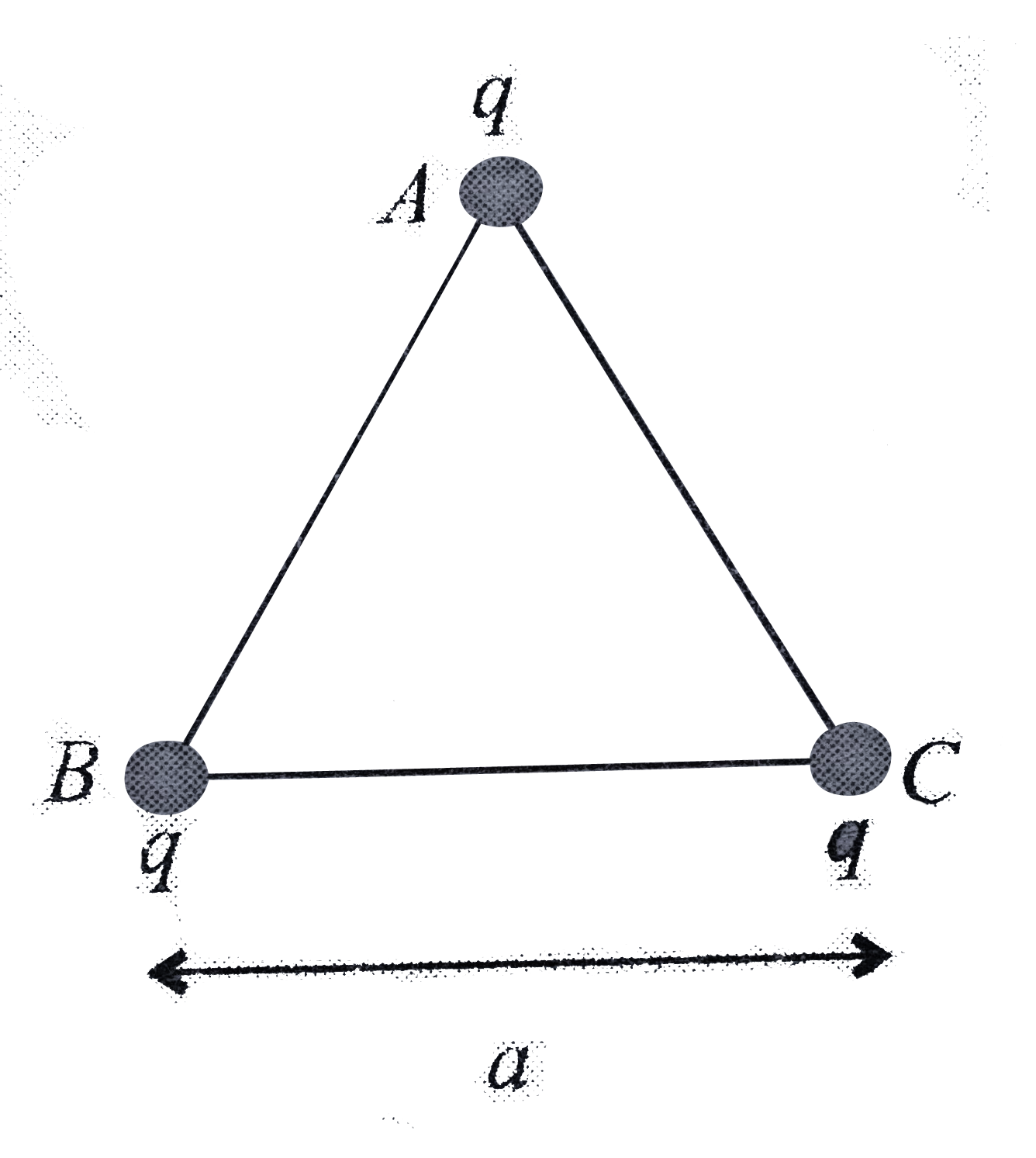
Three equal charges q are placed at the corners of an equilateral triangle of side A.
(i) Find out potential energy of charge system.
(ii) Calculate work required to decrease the side of triangle to a/2.
(iii) If the charges are released from the shown position and each of them has same mass m, then find the speed of each particle when they lie on triangle of side 2a.
 .
.
View SolutionThree equal charges q are placed at the corners of an equilateral triangle of side A.
(i) Find out potential energy of charge system.
(ii) Calculate work required to decrease the side of triangle to a/2.
(iii) If the charges are released from the shown position and each of them has same mass m, then find the speed of each particle when they lie on triangle of side 2a.
 .
.
View SolutionThree identical charges are placed at the vertices of an equilateral triangle. The force experienced by each charge, (if k=14πε0) is
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View SolutionThree equal charge q0 each are placed at three corners of an equilateral triangle of side 'a'. Find out force acting on one of the charge due to other two charges ?
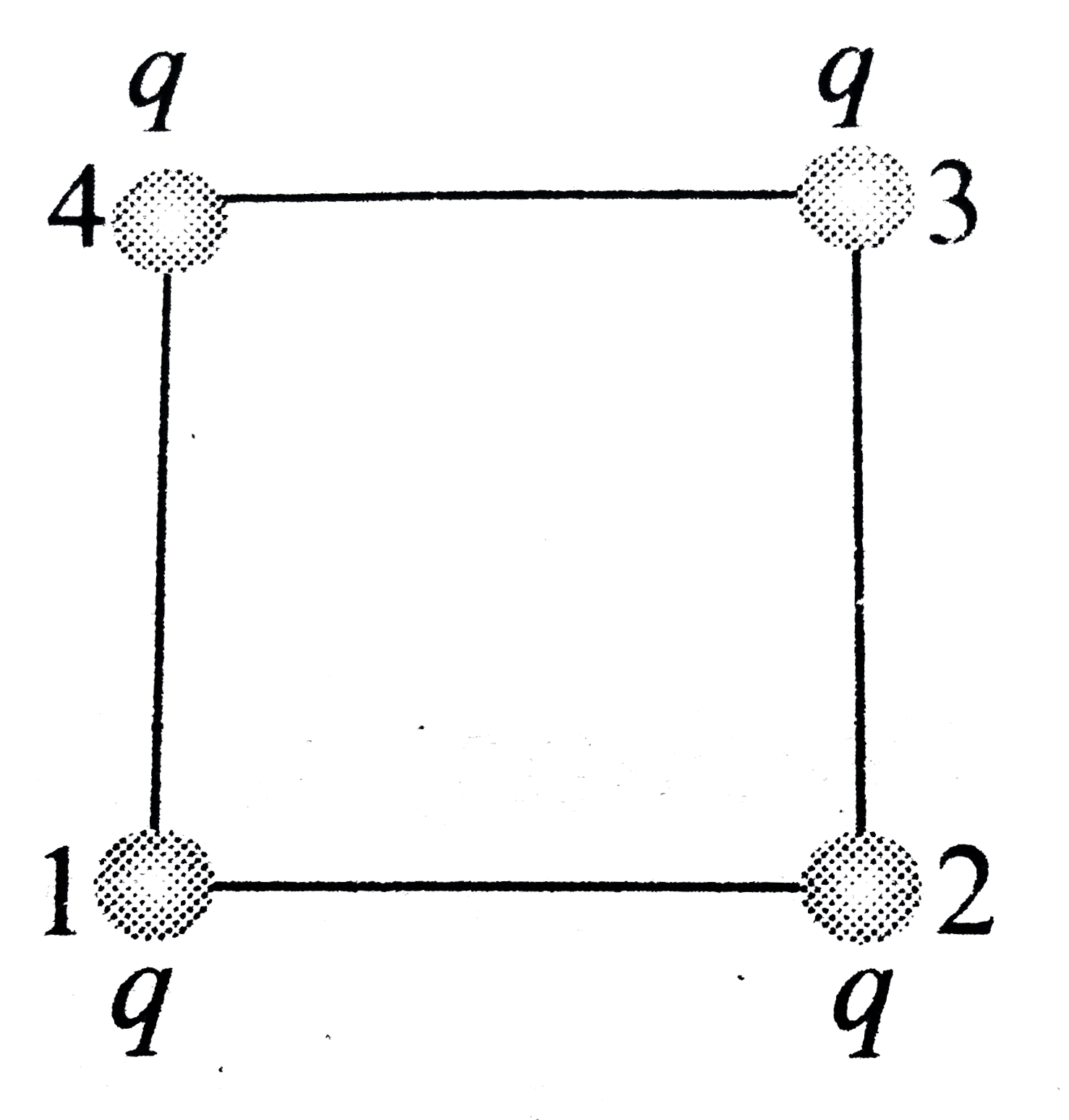
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionThree identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
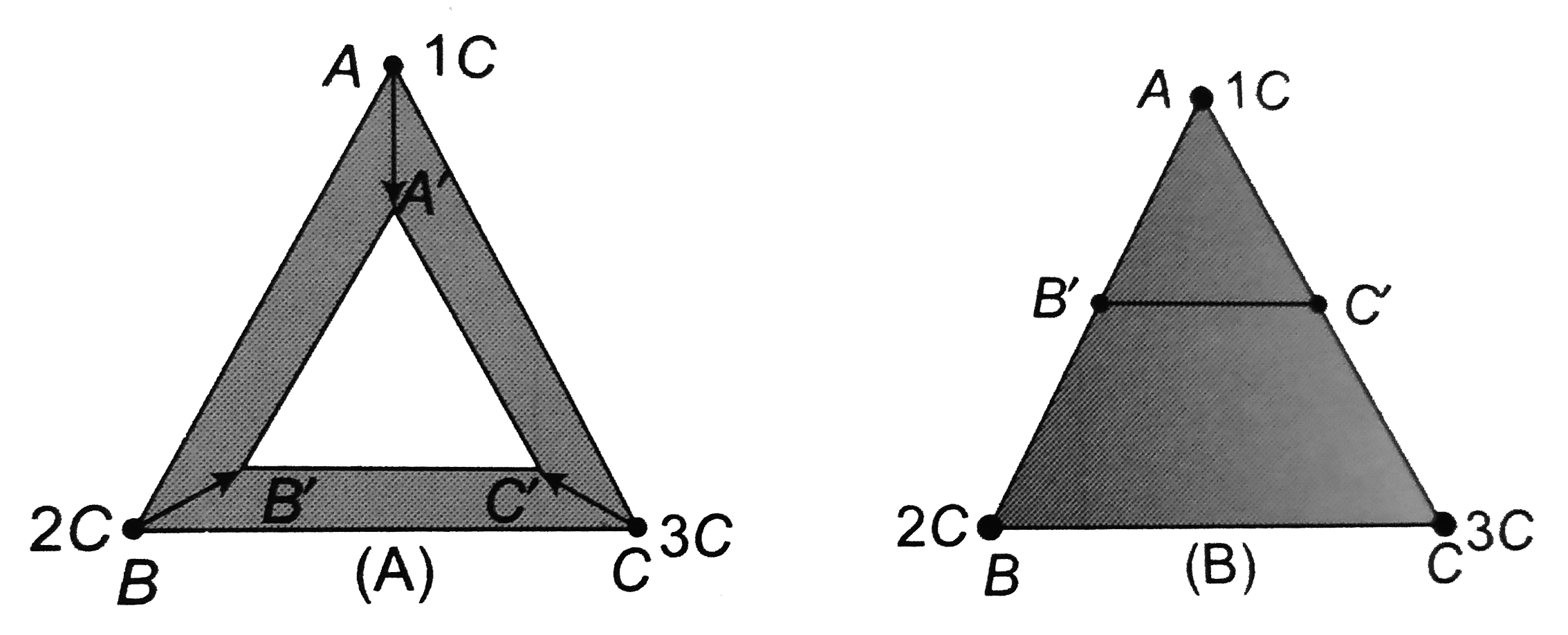
View SolutionThree point charges 1C,2C and 3C are placed at the corners of an equilaternal triangle of side 1m. The work required to move these charges to the corners of a smaller equilaternal triangle of side 0.5m in two differenct ways as in fig. (A) and fig. (B) are Wa and Wb then:
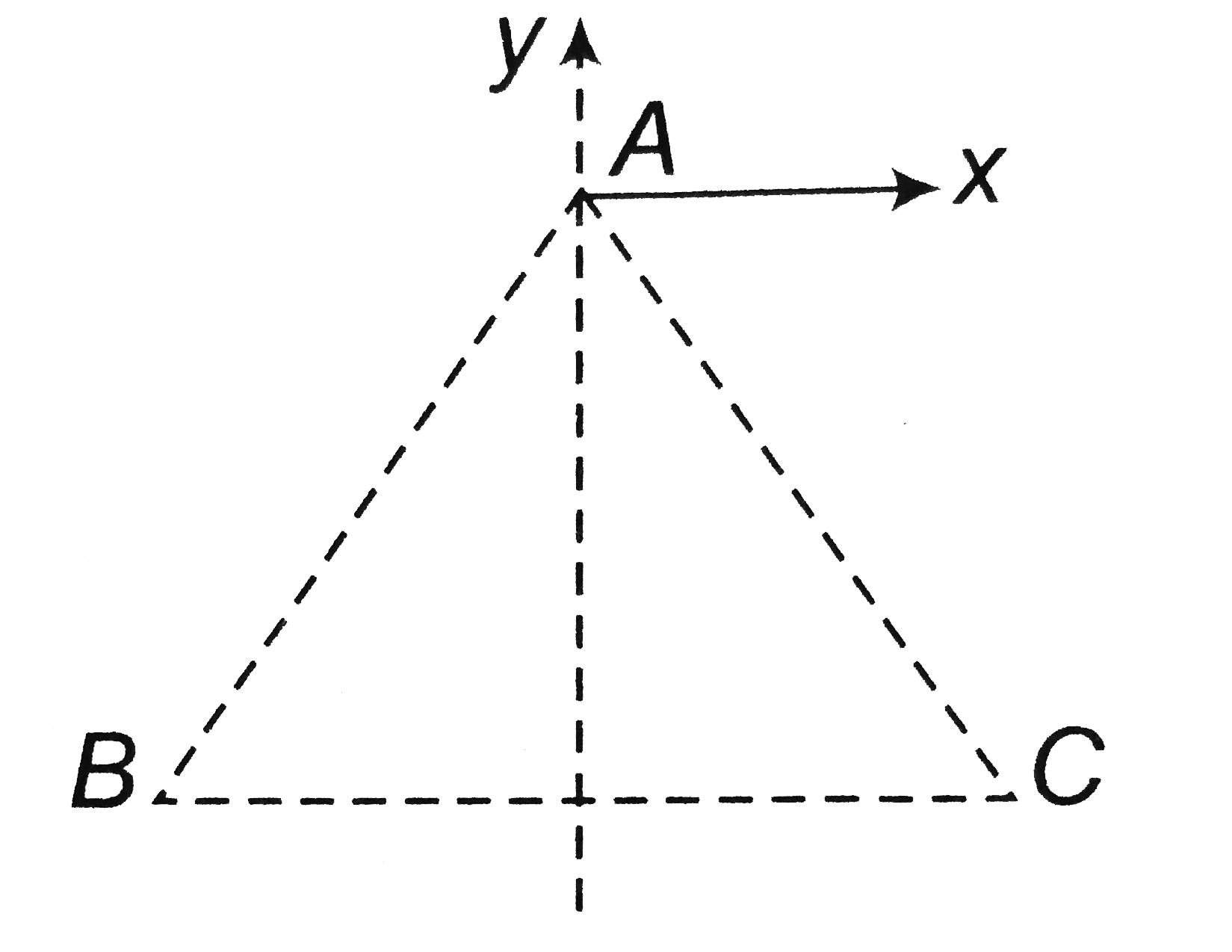
View SolutionThree similar charges +q are placed on 3 corners of an equilateral triangle ABC of side a. How many minimum charges should be placed on a circle of radius a with centre at A so that resultant force on the charge placed at the centre is q24πε0a2 along x-axis,
View Solution
