A small fish 0.4 m below the surface of a lake is viewed through a simple converging lens of focal length 3 m.the lens is kep at 0.2 m above the water surface such that the fish lies on the optical axis of the lens. Find the image of the fish seen by the observed. (μwater=43)
A distance of 0.2 m from the water surface
A distance of 0.6 m from the water surface
A distance of 0.3 m from the water surface
The same location of fish
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Determine the Apparent Depth of the Fish
The fish is located 0.4 m (or 40 cm) below the surface of the water. The apparent depth (d') can be calculated using the formula:
d′=dμ
where d is the actual depth and μ is the refractive index of water.
Given:
- d=40cm
- μ=43
Calculating the apparent depth:
d′=40cm43=40×34=30cm
Step 2: Calculate the Object Distance (U) for the Lens
The lens is positioned 0.2 m (or 20 cm) above the water surface. Therefore, the total distance from the lens to the fish (which is now at the apparent depth of 30 cm) is:
U=apparent depth+height of lens above water
U=30cm+20cm=50cm
Since the object is on the same side as the incoming light, we take U to be negative:
U=−50cm
Step 3: Apply the Lens Formula
The lens formula is given by:
1f=1v−1u
where:
- f is the focal length of the lens,
- v is the image distance,
- u is the object distance.
Given:
- f=3m=300cm
Substituting the values into the lens formula:
1300=1v−1−50
This simplifies to:
1300=1v+150
Step 4: Solve for v
Rearranging the equation gives:
1v=1300−150
Finding a common denominator (which is 300):
1v=1300−6300=1−6300=−5300
Thus,
v=−60cm
Step 5: Interpret the Result
The negative sign indicates that the image is formed on the same side as the object (the fish). This means that the observer sees the fish at a distance of 60 cm from the lens, which is in the direction opposite to the incoming light.
Final Answer
The image of the fish seen by the observer is at a distance of 60 cm from the lens, on the same side as the fish.
---
The fish is located 0.4 m (or 40 cm) below the surface of the water. The apparent depth (d') can be calculated using the formula:
d′=dμ
where d is the actual depth and μ is the refractive index of water.
- d=40cm
- μ=43
d′=40cm43=40×34=30cm
The lens is positioned 0.2 m (or 20 cm) above the water surface. Therefore, the total distance from the lens to the fish (which is now at the apparent depth of 30 cm) is:
U=apparent depth+height of lens above water
U=30cm+20cm=50cm
Since the object is on the same side as the incoming light, we take U to be negative:
U=−50cm
The lens formula is given by:
1f=1v−1u
where:
- f is the focal length of the lens,
- v is the image distance,
- u is the object distance.
- f=3m=300cm
1300=1v−1−50
This simplifies to:
1300=1v+150
Rearranging the equation gives:
1v=1300−150
1v=1300−6300=1−6300=−5300
Thus,
v=−60cm
The negative sign indicates that the image is formed on the same side as the object (the fish). This means that the observer sees the fish at a distance of 60 cm from the lens, which is in the direction opposite to the incoming light.
The image of the fish seen by the observer is at a distance of 60 cm from the lens, on the same side as the fish.
Topper's Solved these Questions
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.5
13 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.6
12 Videos
- RAY OPTICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RAY OPTICSEXERCISE - DPP 1.3
14 Videos
- PHOTOELECTRIC EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type
4 Videos
- SOURCES OF MAGNETIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOURCES OF MAGNETIC FIELDEXERCISE - single correct Ansewer type
12 Videos
Similar Questions
A fish in a lake (refractive index 4/3 for water ) is viewed through a convex lens. From water surface, the lens is placed in air at half of the distance of the fish from the water surface, so that the image is formed at the fish itself. The focal length of the lens is how many times the depth of fish in water?
View SolutionA stationary observer O looking at a fish F in water (μw=4/3) through a converging lens of focal length 90.0cm . The lens is allowed to fall frelly from a height 62.0cm with its axis vertical. The fish and the observer are on the principal axis of the lens. The fish moves up with constant velocity 100cm/s. Initially it was at depth of 44.0cm . Find the velocity (in cm//s) with which the fish appears to move with respect to lens to the observer at t=0.2s. (take g=10m/s2)
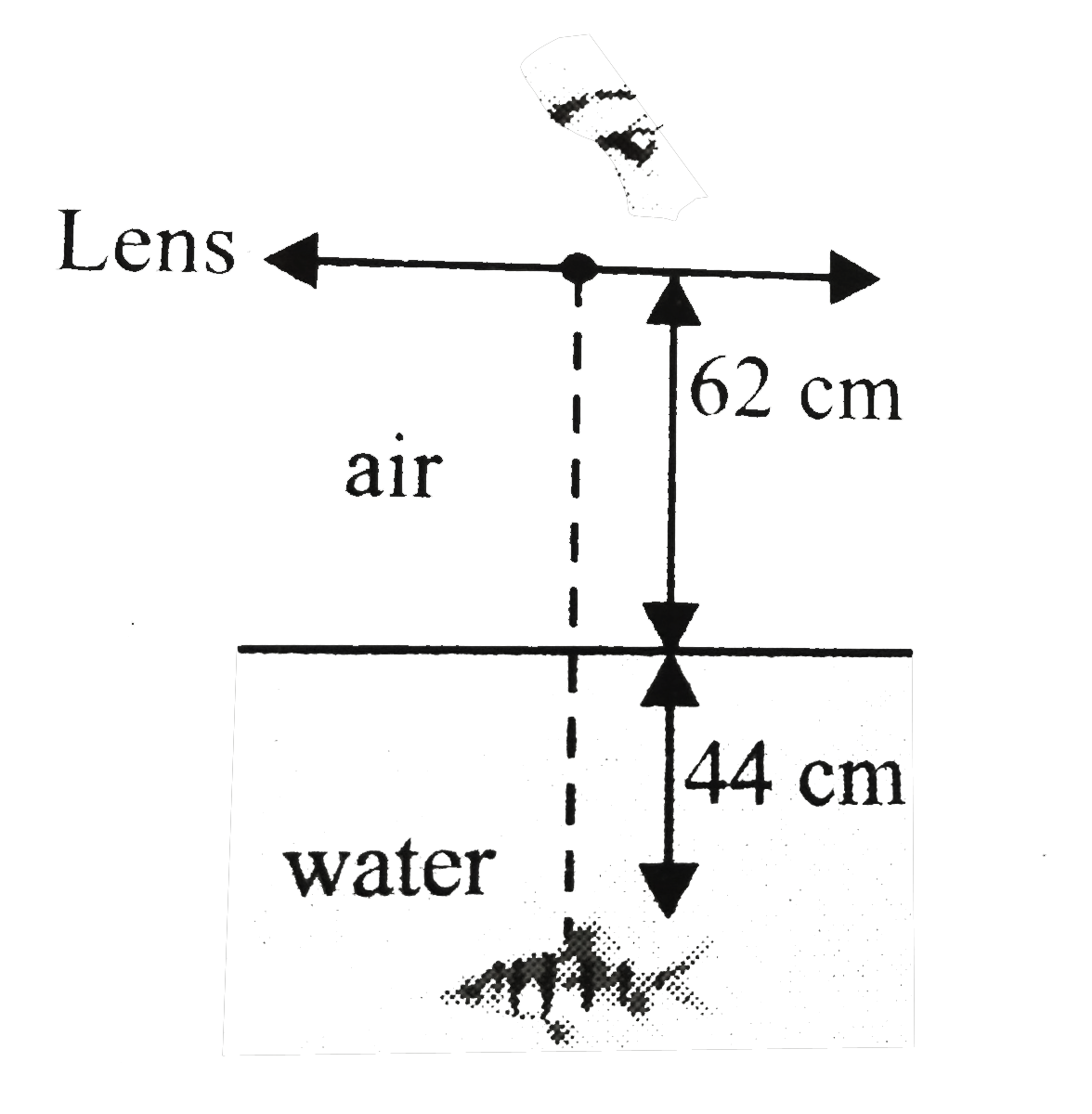
View Solution
Knowledge Check
A convex lens of focal legnth 0.2m and made of glass (μ=1.50) is immersed in water (μ=1.33). Find the change in the focal length of the lens.
A5.8mB0.58cmC0.58mD5.8cmA convergent beam of light passes through a diverging lens of focal length 0.2m and comes to focus at a distance of 0.3m behind the lens. Find the position of the point at which the beam would converge in the absence of the lens.
A0.12mB0.6mC0.3mD0.15m
An object is at a distance of 20 m form a convex lens of focal length 0.3m The lens forms an image of the object moves away form the lens at a speed of 5m/s the speed and direction of the image will be :
View SolutionA pin of length 1cm lies along the principle axis of a converging lens, the centre being at a distance of 5,5cm form the lens. The focal length of the lens is 3cm. Find the size of the image.
View SolutionA plano convex lens has radius of curvature 10 cm. Its focal length is 80 cm under water. Calculate the refractive index of the material of the lens, given refractive index of water is 4/3.
View SolutionA converging lens has a focal length of 0.12 m. To get an image of unit magnification the object should be placed at what distance from the converging lens ?
View SolutionA pin of length 2.0 cm lies along the principal axis of a converging lens, the centre being at a distance of 11 cm from the lens. The focal length of the lens is 6 cm. Find the size of the image.
View SolutionA thin converging lens forms a real image of an object located far away from the lens. The image is formed at A at a distance 4x from the lens and height of the image is h. A thin diverging lens of focal length x is placed at B[PB=2x] and a converging lens of focal length 2x is placed at C[PC=3x]. The principal axes of all lenses coincide. Find the height of the final image formed.
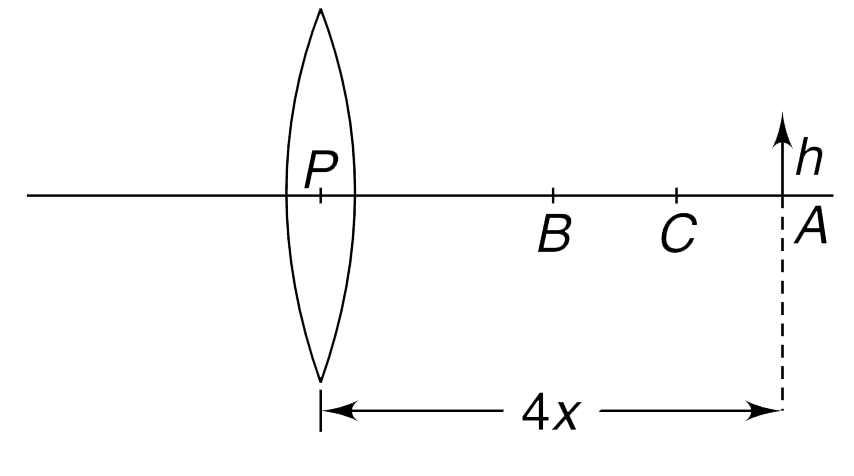
View Solution
