A small object of uniform density rolls up a curved surface with an initial velocity v'. It reaches upto to maximum height of with respect to the initial position. The object is
ring
solid sphere
hollow sphere
disc
The correct Answer is:D
To solve the problem, we need to analyze the energy conservation of the small object as it rolls up the curved surface. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial and Final Energy States
- Initially, the object has kinetic energy due to its velocity v′ and no potential energy since we consider the starting height as the datum (h = 0).
- The total initial energy Ei can be expressed as:
Ei=KEi+PEi=12mv′2+0=12mv′2
Step 2: Determine the Final Energy at Maximum Height
- At the maximum height h=3v′24g, the object momentarily comes to rest, so its kinetic energy becomes zero.
- The potential energy at this height is given by:
PEf=mgh=mg(3v′24g)=34mv′2
- Therefore, the total final energy Ef is:
Ef=KEf+PEf=0+34mv′2=34mv′2
Step 3: Apply Conservation of Energy
- According to the conservation of energy principle, the total initial energy must equal the total final energy:
Ei=Ef
Substituting the expressions we derived:
12mv′2=34mv′2
Step 4: Consider the Rolling Motion
- Since the object is rolling without slipping, we need to account for both translational and rotational kinetic energy. The total kinetic energy when rolling is:
KE=12mv′2+12Iω2
where I is the moment of inertia and ω is the angular velocity. For pure rolling, we have:
ω=v′r
Thus, ω2=v′2r2.
Step 5: Substitute and Rearrange
- The total kinetic energy can be rewritten as:
KE=12mv′2+12I(v′2r2)
- Setting this equal to the potential energy at maximum height:
12mv′2+12I(v′2r2)=34mv′2
Step 6: Solve for Moment of Inertia
- Factor out v′22:
v′22(m+Ir2)=34mv′2
- Dividing both sides by v′2 (assuming v′≠0):
12(m+Ir2)=34m
- Rearranging gives:
m+Ir2=32m
Ir2=32m−m=12m
- Therefore, we find:
I=12mr2
Step 7: Identify the Object
- The moment of inertia I=12mr2 corresponds to a solid disk. Hence, the object is a disk.
Conclusion
The object is a disk (Option 4).
---
- Initially, the object has kinetic energy due to its velocity v′ and no potential energy since we consider the starting height as the datum (h = 0).
- The total initial energy Ei can be expressed as:
Ei=KEi+PEi=12mv′2+0=12mv′2
- At the maximum height h=3v′24g, the object momentarily comes to rest, so its kinetic energy becomes zero.
- The potential energy at this height is given by:
PEf=mgh=mg(3v′24g)=34mv′2
- Therefore, the total final energy Ef is:
Ef=KEf+PEf=0+34mv′2=34mv′2
- According to the conservation of energy principle, the total initial energy must equal the total final energy:
Ei=Ef
Substituting the expressions we derived:
12mv′2=34mv′2
- Since the object is rolling without slipping, we need to account for both translational and rotational kinetic energy. The total kinetic energy when rolling is:
KE=12mv′2+12Iω2
where I is the moment of inertia and ω is the angular velocity. For pure rolling, we have:
ω=v′r
Thus, ω2=v′2r2.
- The total kinetic energy can be rewritten as:
KE=12mv′2+12I(v′2r2)
- Setting this equal to the potential energy at maximum height:
12mv′2+12I(v′2r2)=34mv′2
- Factor out v′22:
v′22(m+Ir2)=34mv′2
- Dividing both sides by v′2 (assuming v′≠0):
12(m+Ir2)=34m
- Rearranging gives:
m+Ir2=32m
Ir2=32m−m=12m
- Therefore, we find:
I=12mr2
- The moment of inertia I=12mr2 corresponds to a solid disk. Hence, the object is a disk.
The object is a disk (Option 4).
Topper's Solved these Questions
Similar Questions

A small object of uniform density rolls up a curved surface with an initial velocity v. It reaches up to a maximum height of 3v24g with respect to the initial position. The object is
(a). Ring
(b). solid sphere
(c). hollow sphere
(d). disc
View SolutionA small object of uniform density rolls up a curved surface with an initial velocity v. it reaches up to a maximum height of (3v^2)/(4g)
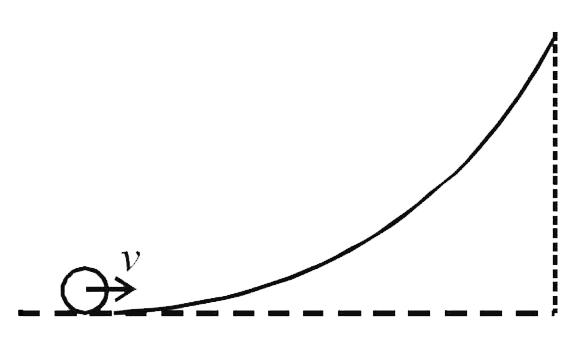
with respect to the initial position. The object is
View Solution
Knowledge Check
A solid cylinder rolls up an inclined plane of inclination θ with an initial velocity v. How far does the cylinder go up the plane ?
A3v22gsinθBv24gsinθC3v2gsinθD3v24gsinθ
A small object of uniform density rolls up a curved surface with an initial velocity v. it reaches up to a maximum height of 3v24g

with respect to the initial position. The object is
View SolutionA small object of uniform density rolls up a curved surface with an initial velocity v. It reached upto maximum height of 3v2/4g with respect to the initial position. The object is -
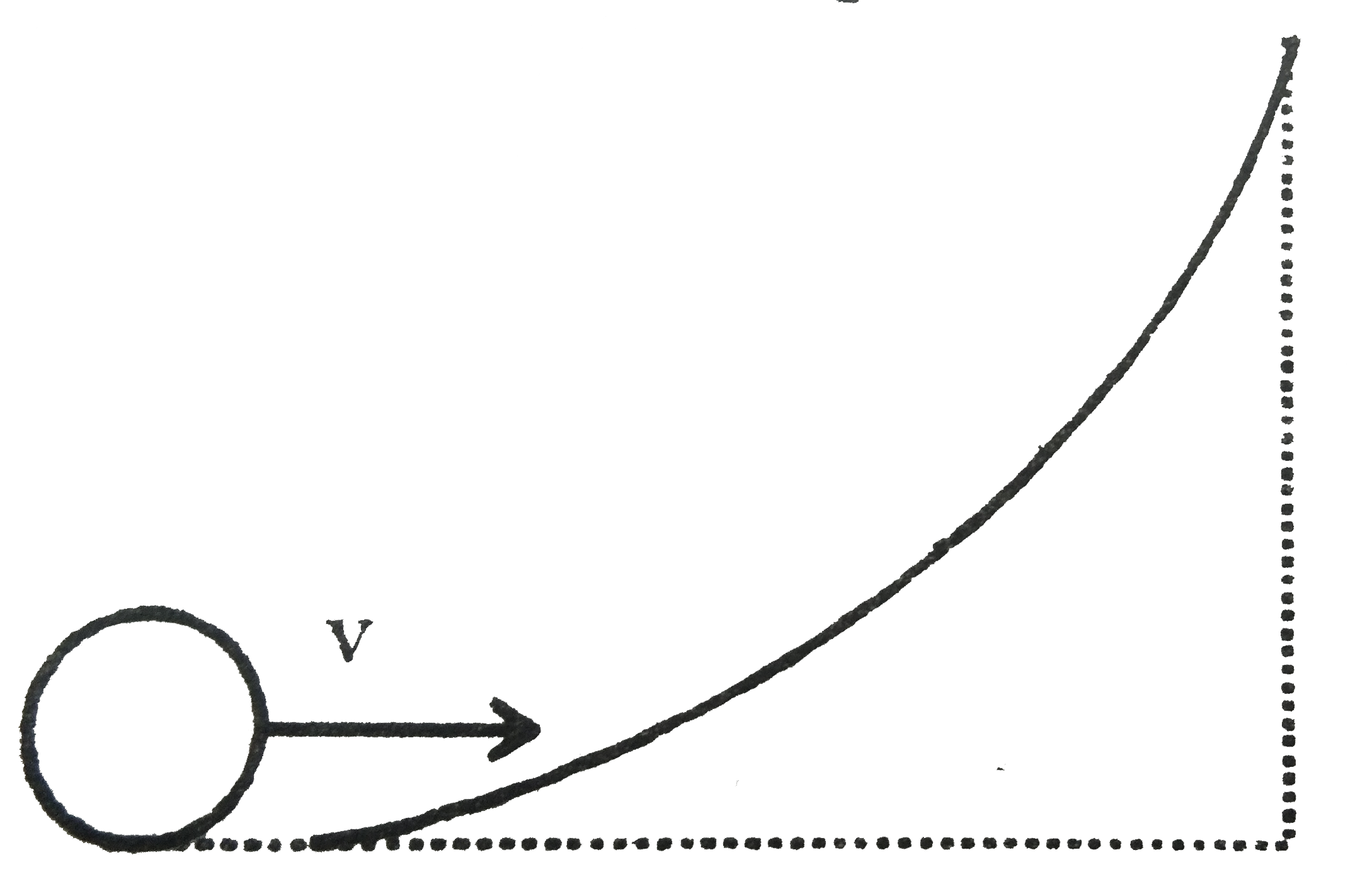 .
.
View SolutionAn object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
View SolutionThe velocity at the maximum height of a projectile is √32 times the initial velocity of projection. The angle of projection is
View SolutionA mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
View SolutionTwo bodies are thrown vertically upwards with their initial velocity in the ratio 2:3. Then the ratio of the maximum height attained by them is
View SolutionWhen a ball is thrown up vertically with velocity v0, it reaches a maximum height of h. If one wishes to triple the maximum height then the ball should be thrown with velocity
View Solution
