An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
The correct Answer is:C
To find the moment of inertia of the object rolling up the hill, we will use the principle of conservation of energy. Here’s a step-by-step solution:
Step 1: Identify the initial kinetic energy
The object is rolling without slipping, so it has both translational and rotational kinetic energy. The total initial kinetic energy (KE_initial) can be expressed as:
KEinitial=KEtranslational+KErotational=12Mv2+12Iω2
where:
- M is the mass of the object,
- v is the linear speed,
- I is the moment of inertia,
- ω is the angular velocity.
Step 2: Relate angular velocity to linear speed
For rolling without slipping, the relationship between linear speed v and angular velocity ω is given by:
ω=vR
where R is the radius of the object.
Step 3: Substitute ω in the kinetic energy equation
Substituting ω in the kinetic energy equation gives:
KEinitial=12Mv2+12I(vR)2
This simplifies to:
KEinitial=12Mv2+12Iv2R2
Step 4: Identify the potential energy at maximum height
When the object reaches its maximum height h, all the kinetic energy is converted into potential energy (PE):
PE=Mgh
Given that h=3v24g, we can substitute this into the potential energy equation:
PE=Mg(3v24g)=3Mv24
Step 5: Set the initial kinetic energy equal to potential energy
By conservation of energy:
KEinitial=PE
Substituting the expressions we derived:
12Mv2+12Iv2R2=3Mv24
Step 6: Rearrange the equation to solve for I
Multiply through by 2 to eliminate the fractions:
Mv2+Iv2R2=3Mv22
Now, isolate the term with I:
Iv2R2=3Mv22−Mv2
This simplifies to:
Iv2R2=3Mv22−2Mv22=Mv22
Step 7: Solve for I
Now, we can solve for I:
I=Mv22⋅R2v2=12MR2
Final Answer
The moment of inertia I of the object is:
I=12MR2
The object is rolling without slipping, so it has both translational and rotational kinetic energy. The total initial kinetic energy (KE_initial) can be expressed as:
KEinitial=KEtranslational+KErotational=12Mv2+12Iω2
where:
- M is the mass of the object,
- v is the linear speed,
- I is the moment of inertia,
- ω is the angular velocity.
For rolling without slipping, the relationship between linear speed v and angular velocity ω is given by:
ω=vR
where R is the radius of the object.
Substituting ω in the kinetic energy equation gives:
KEinitial=12Mv2+12I(vR)2
This simplifies to:
KEinitial=12Mv2+12Iv2R2
When the object reaches its maximum height h, all the kinetic energy is converted into potential energy (PE):
PE=Mgh
Given that h=3v24g, we can substitute this into the potential energy equation:
PE=Mg(3v24g)=3Mv24
By conservation of energy:
KEinitial=PE
Substituting the expressions we derived:
12Mv2+12Iv2R2=3Mv24
Multiply through by 2 to eliminate the fractions:
Mv2+Iv2R2=3Mv22
Now, isolate the term with I:
Iv2R2=3Mv22−Mv2
This simplifies to:
Iv2R2=3Mv22−2Mv22=Mv22
Now, we can solve for I:
I=Mv22⋅R2v2=12MR2
The moment of inertia I of the object is:
I=12MR2
Similar Questions
A mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
View SolutionA body of radius R and mass m is rolling smoothly with speed v on a horizontal surface. It then rolls up a hill to a maximum height h. If h=3v2/4g. What might the body be ?
View SolutionA sphere of mass m and radius r rolls on a horizontal plane without slipping with a speed u. Now it rolls up vertically, then maximum height it would be attain will be
View SolutionA body of mass M and radius r, rolling on a smooth horizontal floor with velocity v, rolls up an irregular inclined plane up to a vertical height (3v2/4g). Compute the moment of inertia of the body.
View SolutionA drum of radius R and mass M, rolls down without slipping along an inclined plane of angle θ. The frictional force-
View SolutionA small object of uniform density rolls up a curved surface with an initial velocity v'. It reaches upto to maximum height of 3v24g with respect to the initial position. The object is
View SolutionA circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
View SolutionA small object of uniform density rolls up a curved surface with an initial velocity v. it reaches up to a maximum height of (3v^2)/(4g)
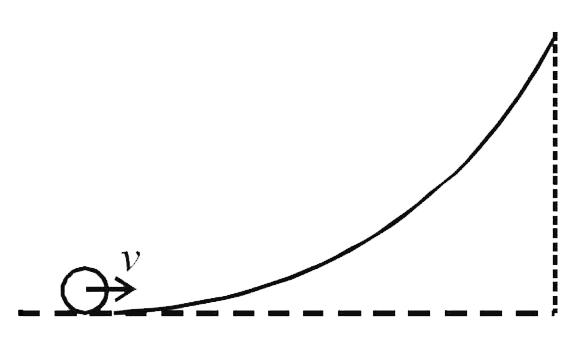
with respect to the initial position. The object is
View SolutionA small object of uniform density rolls up a curved surface with an initial velocity v. it reaches up to a maximum height of 3v24g

with respect to the initial position. The object is
View Solution
A small object of uniform density rolls up a curved surface with an initial velocity v. It reaches up to a maximum height of 3v24g with respect to the initial position. The object is
(a). Ring
(b). solid sphere
(c). hollow sphere
(d). disc
View Solution
