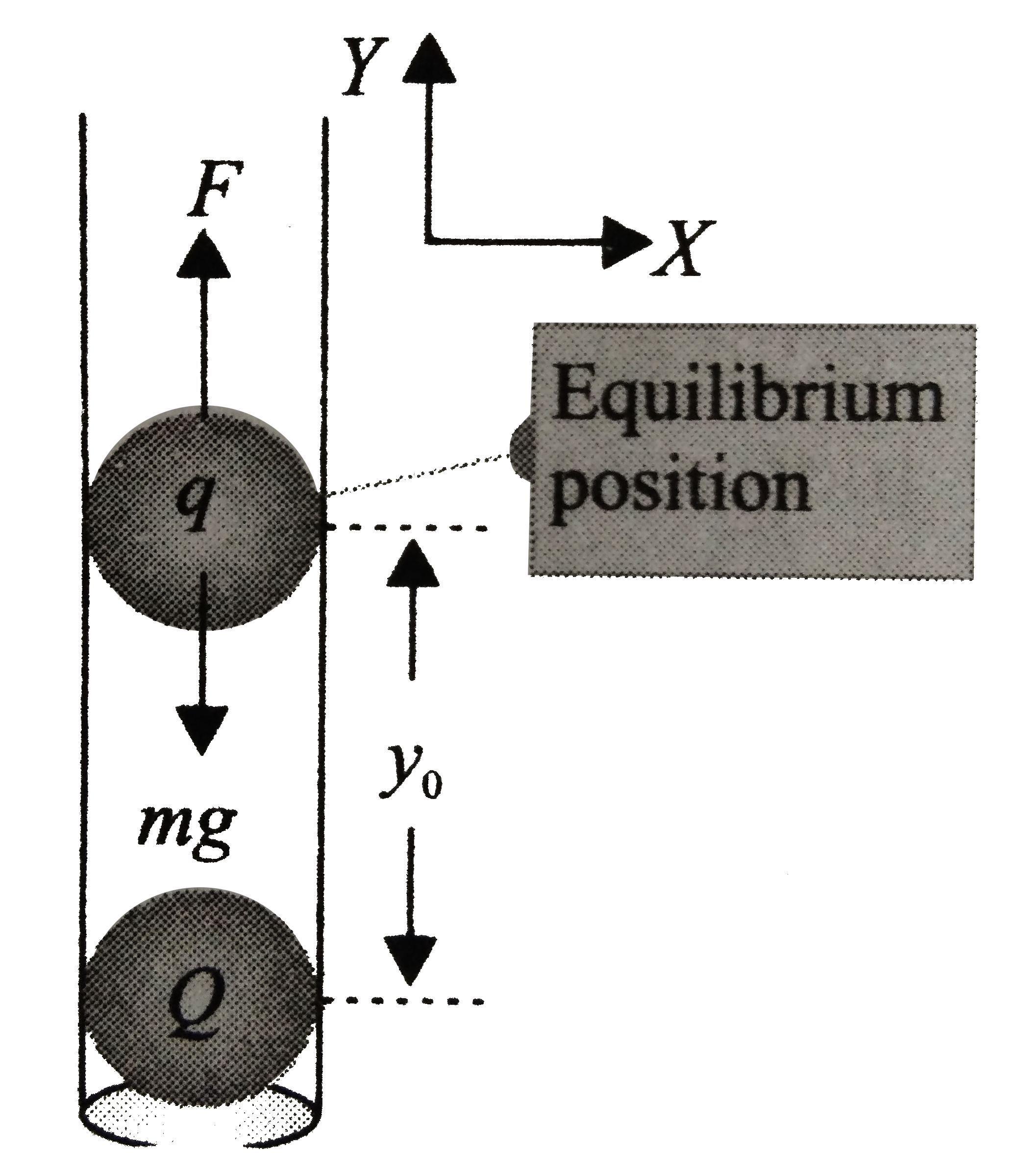
A small point mass m has a charge q, which is constrained to move inside a narrow frictionless cylinder, At the bae of the cylinder is point mass of charge Q having the same sign as q. If the mass m is displaced by a small amount from its equilibrium position and released. it will exhibit simple harmonic motion. Find the angular frequency of the mass?

In the equilibrium position, gravitational force is balanced by Coulomb repulsive force
mg=Qq4πε0y20
If charge q is displaced in positive y-direction such that y<<y0, from Newton's law
Qq4πε0(y0+y)2−mg=ma
or Qq4πε0y20[1(1+y/y0)2]−mg=ma
or mg[1−2yy0]−mg=ma
or a=−2gyy0 or d2ydt2+2gy0y=0
Which is the equation for SHM with ω=√2g/y0.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Exercises
58 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Subjective Type
15 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Answer Correct Type
22 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
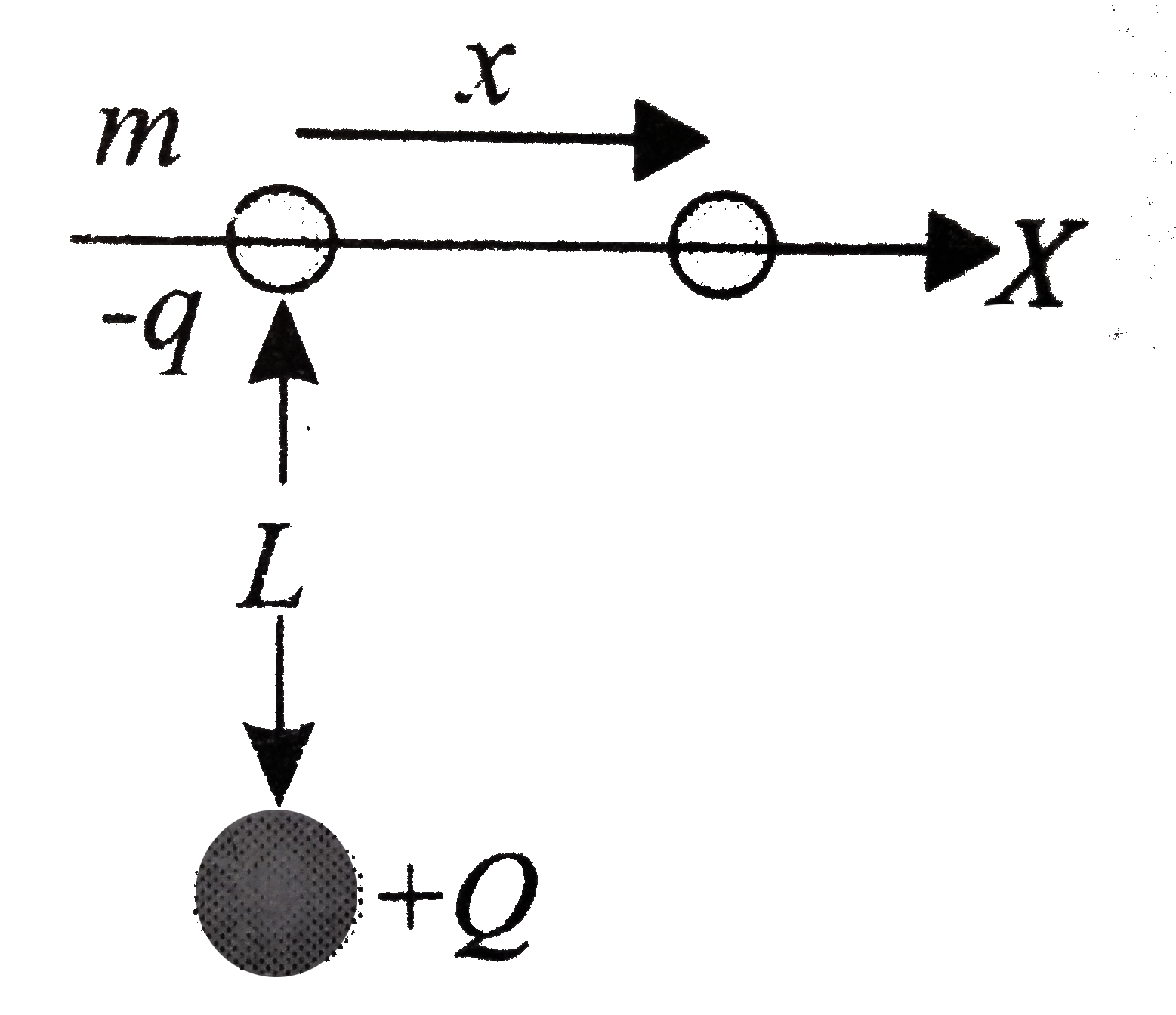
A small beads of mass ma having charge -q is constrained to move along a froctionless wire. A positive charges Q lies at a distance L from the wire. Initiallym the bead is just above charge +Q. Show that if the bead is displaced a distance x, where x<<L, and released, it will exhibit simple harmonic motion. obtain an expression for the tive period of simple harnonic motion.
View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View SolutionFind the time period of mass M when displaced from its equilibrium position and then released for the system shown in figure.

View Solution
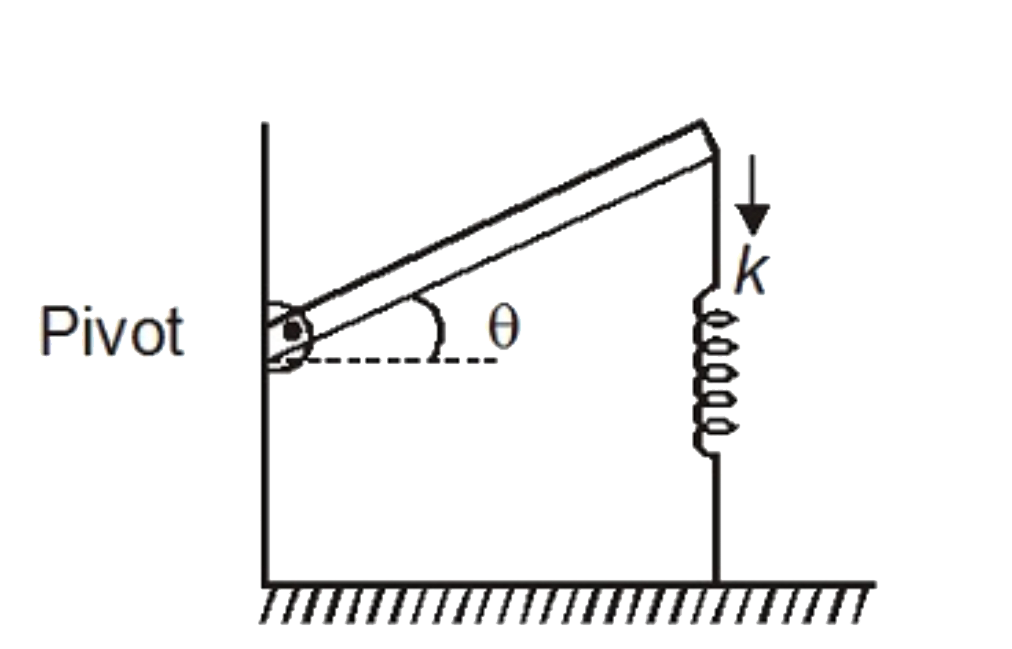
A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion is
View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
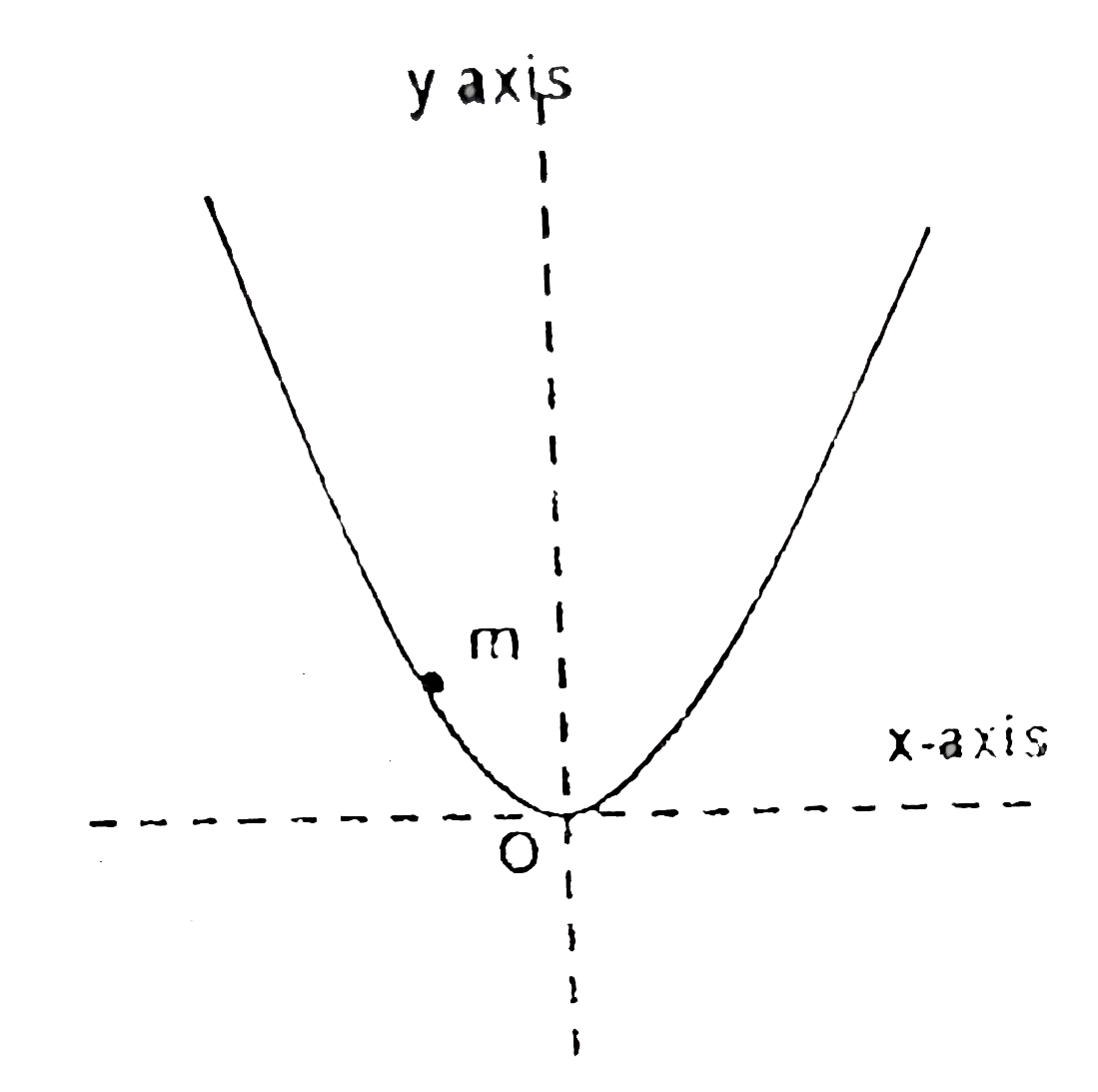
View SolutionA point mass m is displaced slightly from point O and released. It is constrained to move along parabolic path having equation x2=ky then its angular frequency of oscillation is :
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
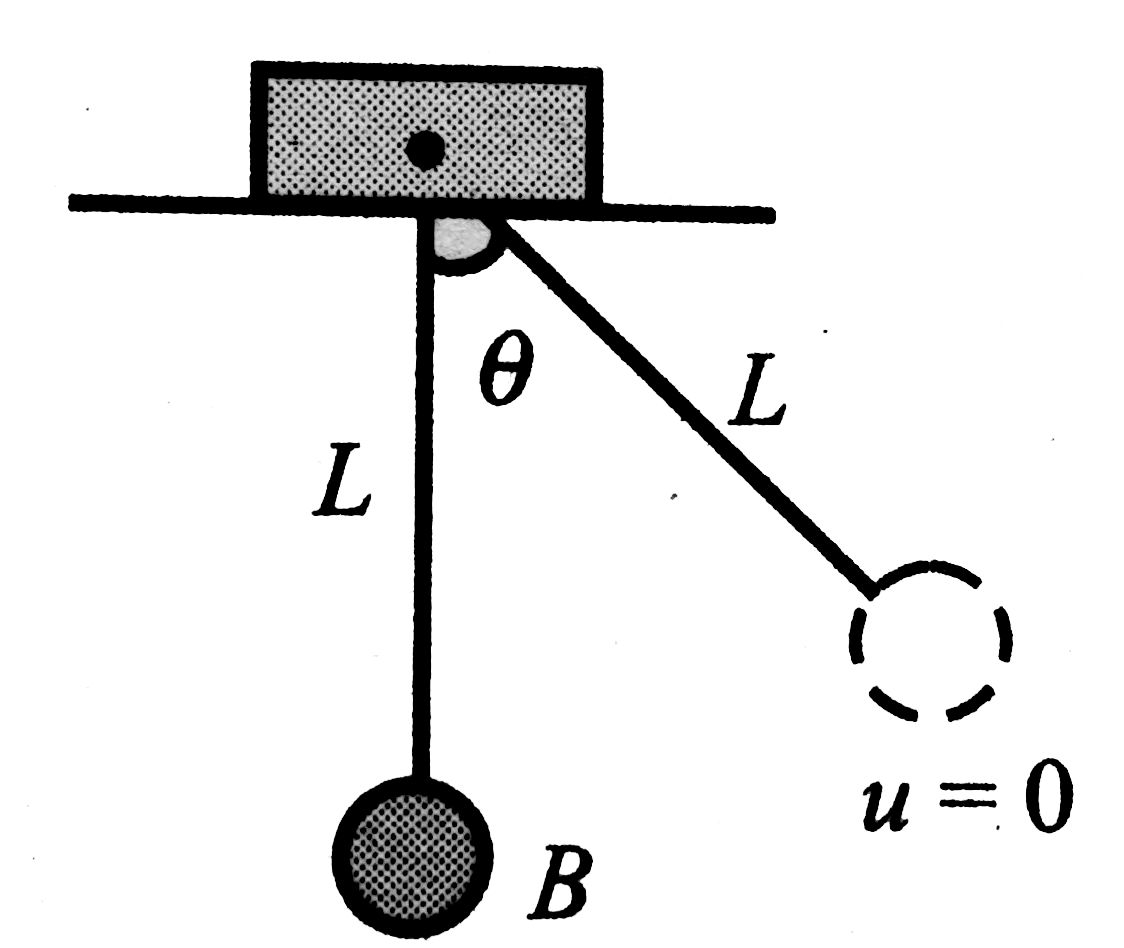
The displacement of block when equilibrium position is
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
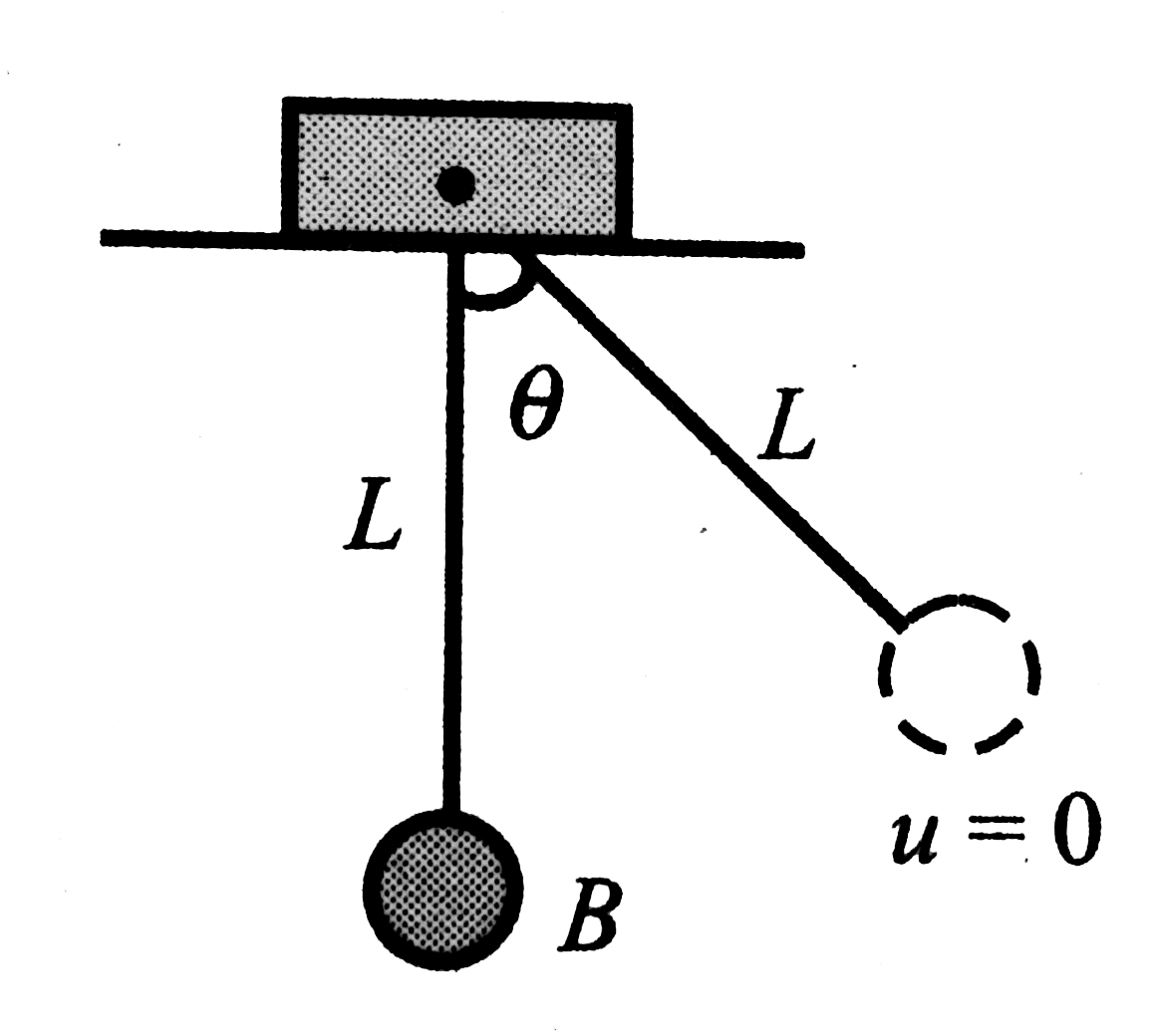 The displacement of centre of mass of A+B system till the string becomes vertical is
The displacement of centre of mass of A+B system till the string becomes vertical is
View SolutionA cylinder piston of mass M sides smoothlly inside a long cylinder closed at and enclesing a cartin mass of gas The cylinder is kept with its axis horizantal if the pistan is distanced from its equations positions it oscillation simple harmoniically .THe period of oscillation will be

View SolutionA particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
View Solution
