A particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and a distance 2l apart. Prove that the motion of the particle will be SHM if it is displaced slightly along the line connecting them and released. Also find its time period.
Let x-y direction is taken as :
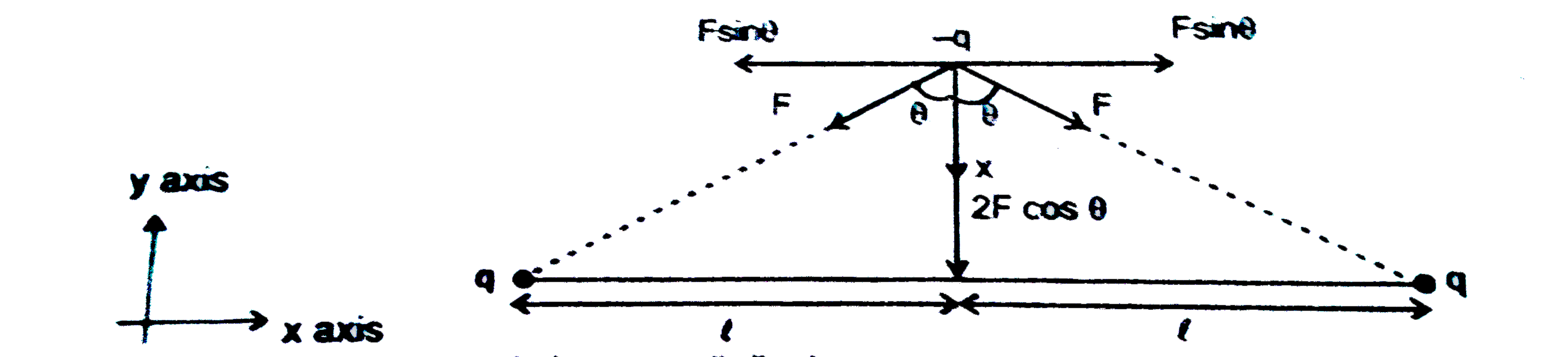
Particle is shifted along y-axis by a small displacement x.
After resolving component of forces between q and -q charges :
By figure. Fnet in x-axis =0 [Fnet= net force on -q charge]
Net force on -q charge in y direction =−2Fcosθ=−2.kqq(x2+l2).x(x2+l2)1/2
∣∣→F∣∣=2Kq2x(x2+l2)3/2 ⇒ ma=2Kq2xl3 (for x<<l) (a=acceleration of -q charge)
⇒a=2Kq2ml2.x(downwards)
This is equation of S.H.M. (a=−ω2x)
So, time period of this charge (-q) :
T=2π√ml32Kq2
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (B)
12 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
A particle of mass m and charge q is located midway between two fixed charged particles each having a charge q and at a distance 2L apart so that distance of this charge from each charge located at end is L. Assuming that the middle charge moves along the line joining the fixed charges. The frequency of oscillation when it is displaced slightly is
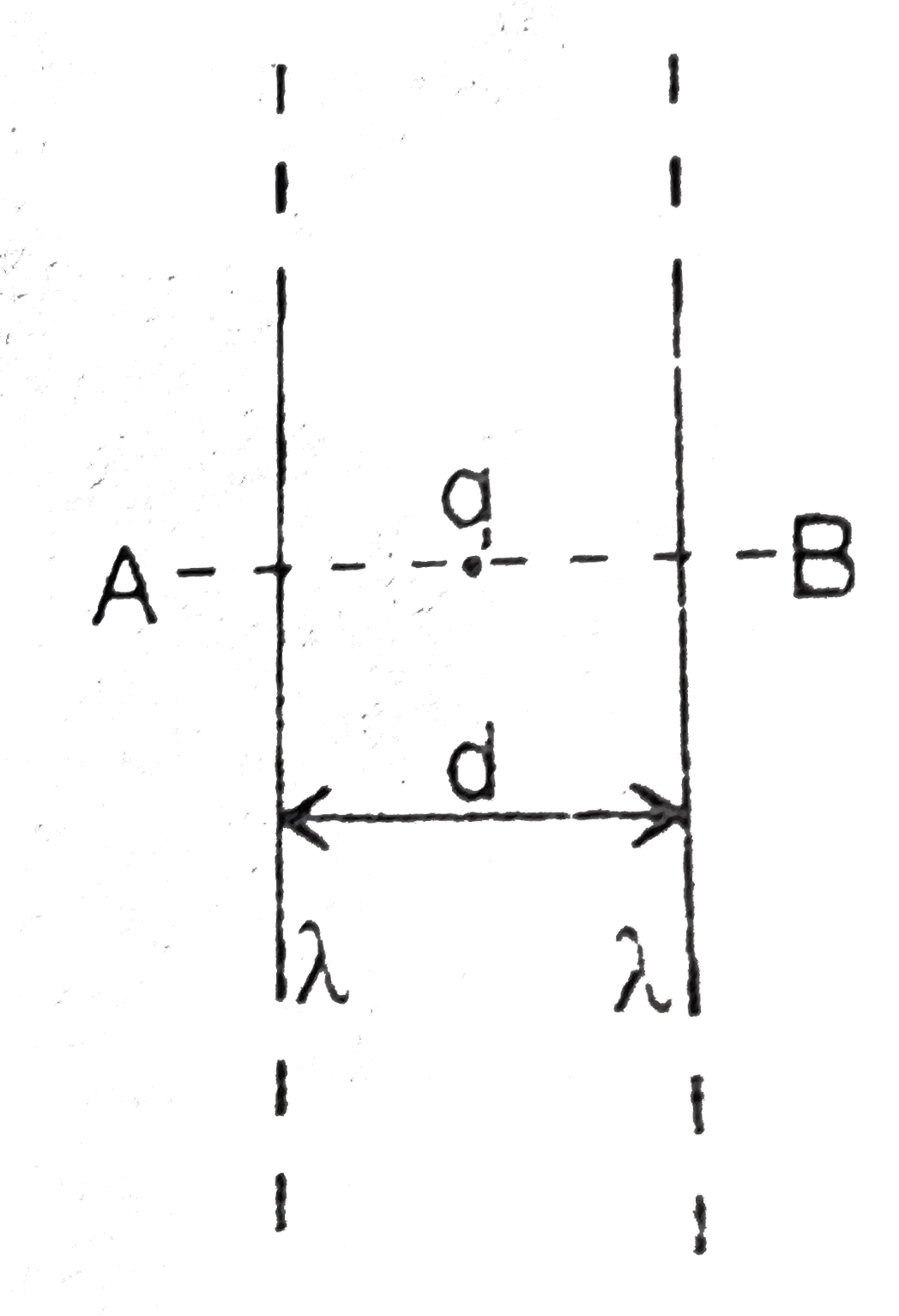
View SolutionTwo infinitely long line charges having charge density λ each are parallel to each other and separated by distance d. A charge particle of mass m and charge q is placed at mid point between them. This charge displaced slightly along a line AB which is perpendicular to the line charges and in the plane of the charges. prove that the motion of the particle will be SHM for small displacement and λq>0 Neglect gravity. Find the time period.
View SolutionA particle of mass .m. and charge q is placed at rest in a uniform electric field E and then released. The K.E. attained by the particle after moving a distance y is
View SolutionA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
View SolutionTwo particles A and B , each carrying charge Q are held fixed with a separation D between them. A particle C having mass m and charge q is kept at the middle point of the line AB. If particle C is displaced through a distance x along the line AB. What will be the time period of the oscillations.
View SolutionA thin fixed ring of radius 'R' and positive charge 'Q' is placed in a vertical plane. A particle of mass 'm' and negative charge 'q' is placed at the centre of ring. If the particle is given a small horizontal displacement, show that it executes SHM. Also find the time period of small oscillations of this particle, about the centre of ring. (Ignore gravity)
View SolutionA particle of mass m carrying a charge −q1 starts moving around a fixed charge +q2 along a circulare path of radius r. Find the time period of revolution T of charge −q1.
View SolutionA charged particle q of mass m is in wquilibrium at a height h from a horizontal infinite line charge wit uniform linear charge density λ. The charge lies in the vertical plane containing the line charge. If the particle is displaced slightly (vertically) prove that the motion of the charged particle will be simple harmonic. Also find its time period.
View SolutionA negatively charged particle is situated on a straight line joining two other stationary particles each having charge +q. The direction of the motion of the negatively charged particle will depend on
View SolutionA charge particle of mass m and charge q is released from rest in uniform electric field. Its graph between velocity (v) and distance travelled (x) will be :
View Solution
