A small signal voltage V(t) = V0 sinωt is applied across an ideal capacitor C.
Over a full cycle the capacitor C does not consume any energy from the voltage source
Current l(t) is in phase with voltage V(t)
Current l(t) leads voltage V(t) by 180∘
Current l(t) leads voltage V(t) by 90∘
The correct Answer is:A
Current is ahead of voltage by 90∘
Power P=VrmsIrmscosρ
=VrmsIrmscos90∘
=VrmsIrms×0
∴ P=0
Topper's Solved these Questions
Similar Questions
A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
View SolutionAn a.c. source generating a voltage v=v+(m)sinωt is connected to a capacitor of capacitor of capacitance C. Find the expression for the current, I, flowing through it. Plot a graph of v and I versus ω t to show that the current is π/2 ahead of the voltage.
A resistor of 200Ω and a capacitor of 15.0μF are connected in series to a 220 V, 50 Hz a.c. source. Calculate the current in the circuit and the rms voltage across the resistor and the capacitor. Is the algebraic sum of these voltages more than the source voltages ? If yes, resolve the paradox.
View Solution
Knowledge Check
A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
ACurrent l(t) leads voltage V(t) by 180∘BCurrent l(t) lags voltage V(t) by 90∘COver a full cycle the capacitor C does not consume any energy from the voltage sourceDCurrent l(t) is in phase with voltage V(t)A small signal voltage V(t)=V0sinωt is applied across an ideal capacitor C:
ACurrent I(t), lags voltage V(t) by 90∘BOver a full cycle the capacitor C does not consume any energy from the voltage source.CCurrent I(t) is in phase with voltage V(t)DCurrent I(t) leads voltage V(t) by 180∘An alternating voltage V=100sinωt is applied across an LCR circuit as shown. At the instant when voltage drop across source is 50√3 volts then at that instant
R=30Ω XL=60Ω XC=20Ω
 Avoltage drop across inductor is (120cos7∘) voltsBvoltage drop across capacitor is (40cos173∘) voltsCvoltage drop across resistor is (60cos7∘) voltsDAll the above
Avoltage drop across inductor is (120cos7∘) voltsBvoltage drop across capacitor is (40cos173∘) voltsCvoltage drop across resistor is (60cos7∘) voltsDAll the above
If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
View SolutionIf an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be
View SolutionA sinusoidal voltage V(t) = 100 sin (500t) is applied across a pure inductance of L = 0.02 H. the current through the coil is
View SolutionA sinusoidal voltage V(t)=100sin(500t) is applied across a pure inductance of L=0.02H. The current through the coil is :
View SolutionAn alternative voltage V=10sinωt (in volts) is applied across a parallel arrangement as shown current (in A) through the source is best described by
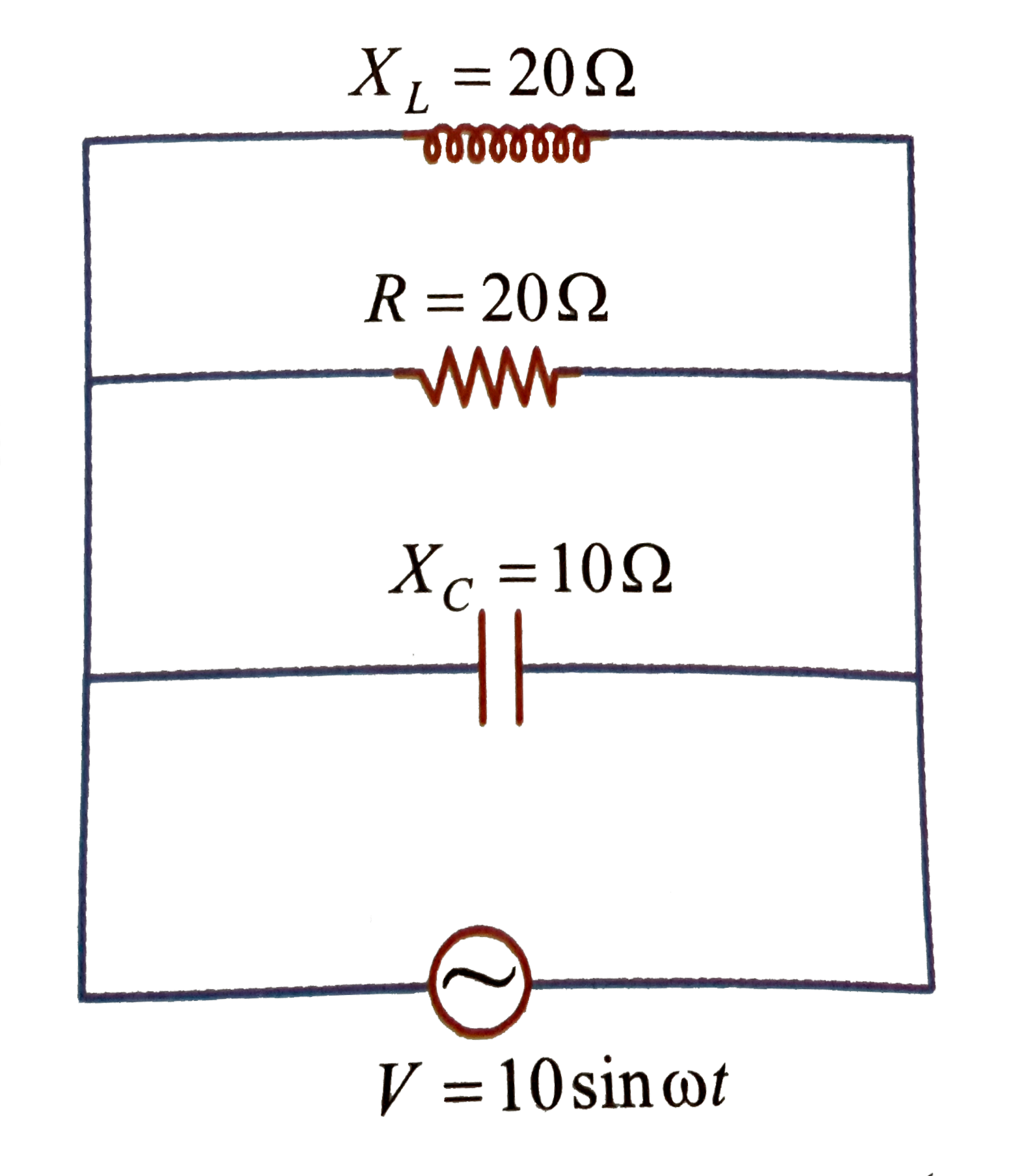
View Solution
