If an alternating voltage V=V_0 sin omegat is applied across an inductance I, the current through the inductance will be

A

$I = I_{0} sin ω t$

B

$I = I_{0} sin (ω t + π / 2)$

C

$I = I_{0} sin (ω t + π / 2)$

D

$I = I_{0} sin (ω t + π)$

Text Solution

Verified by Experts

The correct Answer is:B

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Similar Questions

A circuit contains resistance $R$ and an inductance $L$ in series. An alternating voltage $V = V_{0} sin ω t$ is applied across it. The currents in $R$ and $L$ respectively will be
.
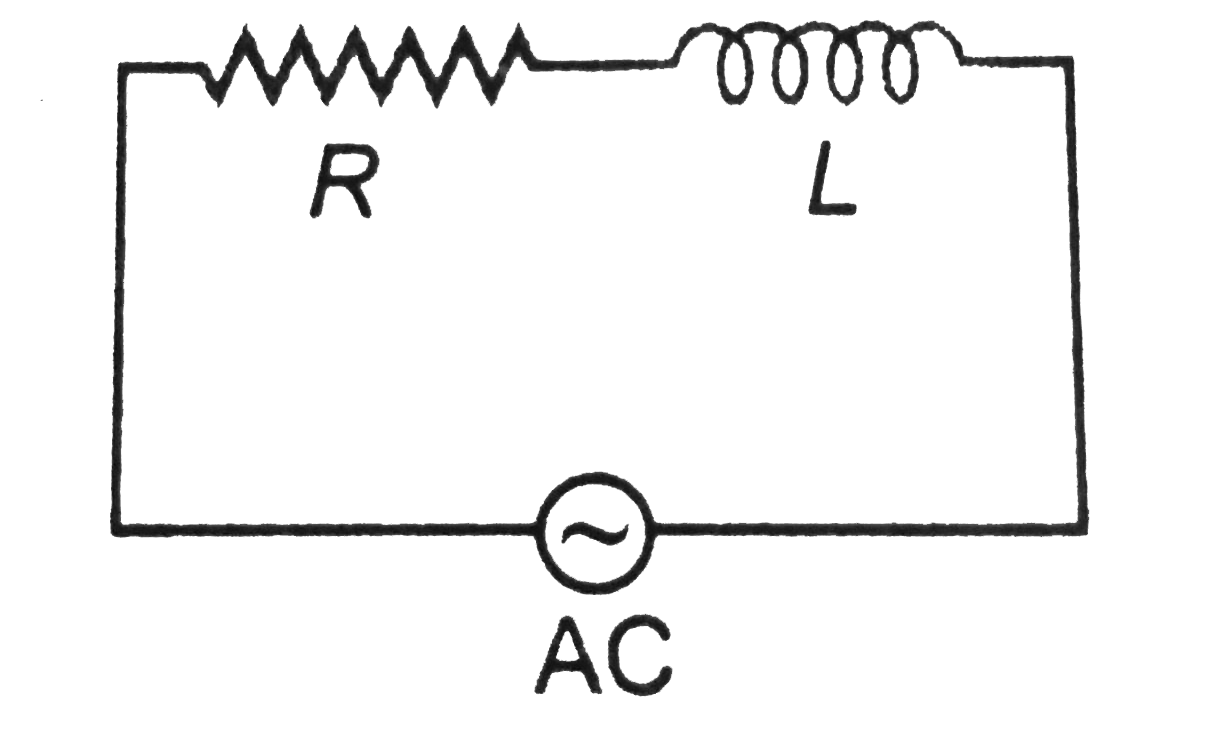View Solution
A circuit contains resistance $R$ and an inductance $L$ in series. An alternating voltage $V = V_{0} sin ω t$ is applied across it. The currents in $R$ and $L$ respectively will be
.
View Solution

Knowledge Check

Question 1 - Select One
A circuit contains resistance $R$ and an inductance $L$ in series. An alternating voltage $V = V_{0} sin ω t$ is applied across it. The currents in $R$ and $L$ respectively will be
.
A $I_{R} = I_{0} cos ω t, I_{L} = I_{0} cos ω t$
B $I_{R} = - I_{0} sin ω, I_{L} = I_{0} cos ω t$
C $I_{R} = I_{0} sin ω, I_{L} = - I_{0} cos ω t$
Dnone of the above
Question 2 - Select One
The alternating emf of $e = e_{0}$ sin $ω t$ is applied across capacitor C. the current through the circuit is given by
A $I = I_{0} sin ω t$
B $I = I_{0} sin (ω t + \frac{π}{2})$
C $I = I_{0} sin (ω t - \frac{π}{2})$
D $I = I_{0} sin (ω t - π)$
Question 3 - Select One
A small signal voltage $V (t) = V_{0} sin ω t$ is applied across an ideal capacitor $C$ :
ACurrent $I (t)$ , lags voltage $V (t)$ by $90^{\circ}$
BOver a full cycle the capacitor $C$ does not consume any energy from the voltage source.
CCurrent $I (t)$ is in phase with voltage $V (t)$
DCurrent $I (t)$ leads voltage $V (t)$ by $180^{\circ}$

Recommended Questions

Home
Ask Doubt
Profile