A small stone of mass m is attached to a light string which passes through a hollow tube. The tube is held by one hand and the free end of the string by the other hand. The mass is set into revolution in a horizontal circle of radius r1 with a speed v1 . The string is pulled down shortening the radius of the circular path to r2. Which of the following is not correct? (ω1 and T have usual meanings)
ω2ω1=r21r22
Ek1Ek2=r22r21
Ek1Ek2=r22r21
T2T1=r31r32
The correct Answer is:D
To solve the problem, we need to analyze the motion of the stone attached to the string as the radius of its circular path changes. We will use the principles of angular momentum and tension in the string.
1. Understanding the Initial Conditions:
- The stone of mass m is revolving in a horizontal circle of radius r1 with speed v1.
- The angular momentum (L) of the stone can be expressed as:
\(
L_1 = m \cdot v_1 \cdot r_1
\)
2. Changing the Radius:
- When the string is pulled down, the radius changes from r1 to r2, and the speed changes from v1 to v2.
- Since there is no external torque acting on the system, the angular momentum is conserved:
\(
L_1 = L_2 \implies m \cdot v_1 \cdot r_1 = m \cdot v_2 \cdot r_2
\)
- We can cancel the mass m from both sides (assuming it remains constant):
\(
v_1 \cdot r_1 = v_2 \cdot r_2
\)
3. Relating Speeds and Radii:
- Rearranging the equation gives us the relationship between the speeds and the radii:
\(
\frac{v_1}{v_2} = \frac{r_2}{r_1}
\)
- This implies:
\(
v_2 = v_1 \cdot \frac{r_2}{r_1}
\)
4. Tension in the String:
- The tension in the string can be expressed in terms of the speed and radius:
\(
T = \frac{m \cdot v^2}{r}
\)
- For the two states, we have:
\(
T_1 = \frac{m \cdot v_1^2}{r_1} \quad \text{and} \quad T_2 = \frac{m \cdot v_2^2}{r_2}
\)
5. Finding the Ratio of Tensions:
- To find the ratio of tensions:
\(
\frac{T_2}{T_1} = \frac{v_2^2 \cdot r_1}{v_1^2 \cdot r_2}
\)
- Substituting \( v_2 = v_1 \cdot \frac{r_2}{r_1} \):
\(
\frac{T_2}{T_1} = \frac{\left(v_1 \cdot \frac{r_2}{r_1}\right)^2 \cdot r_1}{v_1^2 \cdot r_2} = \frac{r_2^2 \cdot r_1}{r_1^2 \cdot r_2} = \frac{r_2}{r_1}
\)
6. Angular Velocity Relation:
- The angular velocity is related to linear velocity and radius:
\(
\omega = \frac{v}{r}
\)
- For the two states:
\(
\frac{\omega_2}{\omega_1} = \frac{v_2/r_2}{v_1/r_1} = \frac{v_2 \cdot r_1}{v_1 \cdot r_2}
\)
- Substituting \( v_2 = v_1 \cdot \frac{r_2}{r_1} \):
\(
\frac{\omega_2}{\omega_1} = \frac{\left(v_1 \cdot \frac{r_2}{r_1}\right) \cdot r_1}{v_1 \cdot r_2} = \frac{r_2}{r_1}
\)
7. Conclusion:
- After analyzing the options, we find that the only incorrect statement is option A, which does not conform to the derived relationships.
Final Answer:
The option that is not correct is A.
- The stone of mass m is revolving in a horizontal circle of radius r1 with speed v1.
- The angular momentum (L) of the stone can be expressed as:
\(
L_1 = m \cdot v_1 \cdot r_1
\)
- When the string is pulled down, the radius changes from r1 to r2, and the speed changes from v1 to v2.
- Since there is no external torque acting on the system, the angular momentum is conserved:
\(
L_1 = L_2 \implies m \cdot v_1 \cdot r_1 = m \cdot v_2 \cdot r_2
\)
- We can cancel the mass m from both sides (assuming it remains constant):
\(
v_1 \cdot r_1 = v_2 \cdot r_2
\)
- Rearranging the equation gives us the relationship between the speeds and the radii:
\(
\frac{v_1}{v_2} = \frac{r_2}{r_1}
\)
- This implies:
\(
v_2 = v_1 \cdot \frac{r_2}{r_1}
\)
- The tension in the string can be expressed in terms of the speed and radius:
\(
T = \frac{m \cdot v^2}{r}
\)
- For the two states, we have:
\(
T_1 = \frac{m \cdot v_1^2}{r_1} \quad \text{and} \quad T_2 = \frac{m \cdot v_2^2}{r_2}
\)
- To find the ratio of tensions:
\(
\frac{T_2}{T_1} = \frac{v_2^2 \cdot r_1}{v_1^2 \cdot r_2}
\)
- Substituting \( v_2 = v_1 \cdot \frac{r_2}{r_1} \):
\(
\frac{T_2}{T_1} = \frac{\left(v_1 \cdot \frac{r_2}{r_1}\right)^2 \cdot r_1}{v_1^2 \cdot r_2} = \frac{r_2^2 \cdot r_1}{r_1^2 \cdot r_2} = \frac{r_2}{r_1}
\)
- The angular velocity is related to linear velocity and radius:
\(
\omega = \frac{v}{r}
\)
- For the two states:
\(
\frac{\omega_2}{\omega_1} = \frac{v_2/r_2}{v_1/r_1} = \frac{v_2 \cdot r_1}{v_1 \cdot r_2}
\)
- Substituting \( v_2 = v_1 \cdot \frac{r_2}{r_1} \):
\(
\frac{\omega_2}{\omega_1} = \frac{\left(v_1 \cdot \frac{r_2}{r_1}\right) \cdot r_1}{v_1 \cdot r_2} = \frac{r_2}{r_1}
\)
- After analyzing the options, we find that the only incorrect statement is option A, which does not conform to the derived relationships.
The option that is not correct is A.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
View SolutionA body of mass 100 g is rotating in a circular path of radius r with constant speed. The work done in one complete revolution is
View Solution
Knowledge Check
- Question 1 - Select One
A stone tied to the end of string 100cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolution in 22s, then the acceleration of the stone is
A16 m s−2B4 m s−2C12 m s−2D8 m s−2
A mass m is attached to a string passing through a small hole in a frictionless, horizontal surface. The mass is initially orbiting with a velocity v1 in a circle of radius r1 The string is then slowly pulled from below, decreasing the radius of the circles to r2 (i) What is the speed of the mass when the radius is r2 ? (ii) What is the tension in the string ? (iii) What is the work done in moving the mass m from r1 to r2?
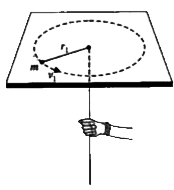 View Solution
View SolutionA block of mass m is attached to one end of a light string which is wrapped on a disc of mass 2m and radius R. The total length of the slack portion of the string is l. The block is released from rest. The angular velocity of the disc just after the string becomes taut is
 View Solution
View SolutionA mass m rests on a horizontal table. It is attached to a light inextensible string which passes over a smooth pulley and carries a mass m at the other end. If the mass m is raised vertically through a distance h and is then dropped, what is the speed with which the mass 2m begins to rise?
 View Solution
View SolutionA stone of mass 0.5 kg is attached to a string of length 2 m and is whirled in a horizontal circle. If the string can with stand a tension of 9N, the maximum velocity with which the stone can be whirled is:
View SolutionAn object of mass 10kg is attached to roof by string whirled round a horizontal circle of radius 4 and 30∘ to the vertical. The tension in the string (approximately) is
View SolutionA particle of mass 200g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g=10ms2)
View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png) View Solution
View Solution
