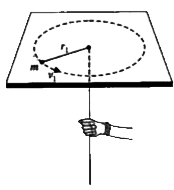
A mass m is attached to a string passing through a small hole in a frictionless, horizontal surface. The mass is initially orbiting with a velocity v1 in a circle of radius r1 The string is then slowly pulled from below, decreasing the radius of the circles to r2 (i) What is the speed of the mass when the radius is r2 ? (ii) What is the tension in the string ? (iii) What is the work done in moving the mass m from r1 to r2?
The correct Answer is:459
The torque acting on the rotating mass about the vertical axis is zero. So law of conservation of angular momentum holds good,
mv1r1=mv2r2
v2=v1r1r2
The tension in the string is T
T=mv22r2=mv21r21r32
The change in K.E. =12mv22−12mv21
=12mv21[r21−r22r22]
The work done in moving the mass from r1 to r2 is equal to change in K.E.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (CONCEPTUAL SHORT ANSWERS QUESTIONS WITH ANSWERS )11videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - CIRCULAR MOTION EXERCISE - MODULE 1 (LONG ANSWER QUESTIONS)8videos
CIRCULAR MOTION
- BOOK - ICSECHAPTER - COMPETITION CARE UNITEXERCISE - OBJECTIVE QUESTIONS FROM PREVIOUS IAS EXAMINATIONS50videos
COMPETITION CARE UNIT
Similar Questions
A small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius 0.5m about the hole with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shorteing the radius of the circle in which the block revolves. The breaking strength of the cord is 600N. What will be radius of the circle when the cord breaks?
 View Solution
View SolutionFigure shows a mass m placed on a frictionless horizontal table and attached toa string passing through a mall hole in the surface. Initially, themas movesin a circle of radius r0 with a speed v0 and the ree end of the string is held by a person. The person pulls on the string slowly to decrease the radius of th circle of r. a. Find the tension in the string when the mass moves in the circle of radius r. b. Calculate the chasnge in the kinetic energy of the mass
View Solution
Knowledge Check
- Question 1 - Select One
A mass is supported on a frictionless horizontal surface. It is attached to a string and rotates about a fixed centre with a angular velocity ω0. If the length of the string and angular velocity are doubled, the tension in the string which was initially T0 is now
AT0BT0/2C4T0D8T0
A small block of mass 4kg is attached to a cord passing through a hole in a horizontal frictionless surface. The block is originally revolving in a circle of radius of 5m about the hole, with a tangential velocity of 4m/s. The cord is then pulled slowly from below, shortening the radius of the circle in which the block revolves. The breaking strength of the cord is 200N.
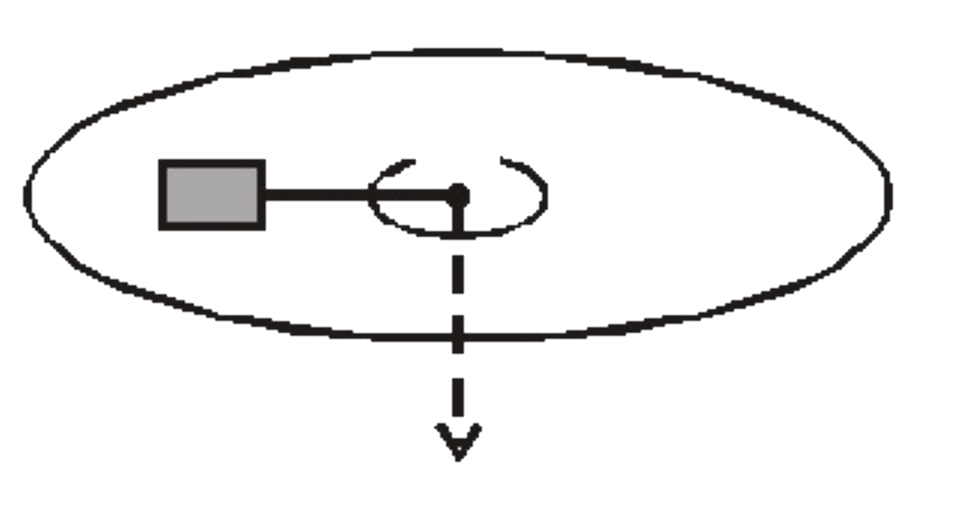
Velocity of the block at the time of breaking of the stringView SolutionA block of mass 0.1 kg is attached to a cord passing through a hole in a horizontal frictionless horizontal surface as shown in the figure. The block is originally revolving at a distance of 0.4 m from the hole, with an angular velocity of 2 rad s−1. The cord is then pulled from below, shortening the radius of the circle in which the block revolves to 0.2 m. Considering the block to be point mass, calculate the new angular velocity (in rad s−1)
 View Solution
View SolutionA small stone of mass 50 g is rotated in a vertical circle of radius 40 cm. What is the minimum tension in the string at the lowest point?
View SolutionA small stone of mass m is attached to a light string which passes through a hollow tube. The tube is held by one hand and the free end of the string by the other hand. The mass is set into revolution in a horizontal circle of radius r1 with a speed v1 . The string is pulled down shortening the radius of the circular path to r2. Which of the following is not correct? (ω1 and T have usual meanings)
View SolutionA body of mass m is made to revolve along a circle of radius r in horizontal plane at a speed Vm/s with help of light horizontal string such that the tension in the string is 10 N. Keeping speed constant if mass is increased to 2m und radius is decreased to r/2 then tension in the string is
View Solutiontwo masses 2m and m are attached to the the ends of a string while passing over a smooth Pulley of mass m and radius R. The ratio of tensions in both the strings is
_PHY_E05_245_Q01.png) View Solution
View SolutionA ball of mass 0.6kg attached to a light inextensible string rotates in a vertical circle of radius 0.75m such that it has speed of 5ms−1 when the string is horizontal. Tension in the string when it is horizontal on other side is (g=10ms−2).
View Solution

