A smooth rod is fixed at an angle α to the horizontal. A small ring of mass m can slide along the rod. A thread carrying a small sphere of mass M is attached to the ring. To keep the system in equilibrium, another thread is attached to the ring which carries a load of mass m0at its end (see figure). The thread runs parallel to the rod between the ring and the pulley. All threads and pulley are massless.
(a) Find m0 so that system is in equilibrium.
(b) Find acceleration of the sphere M immediately after the thread supporting m0 is cut.
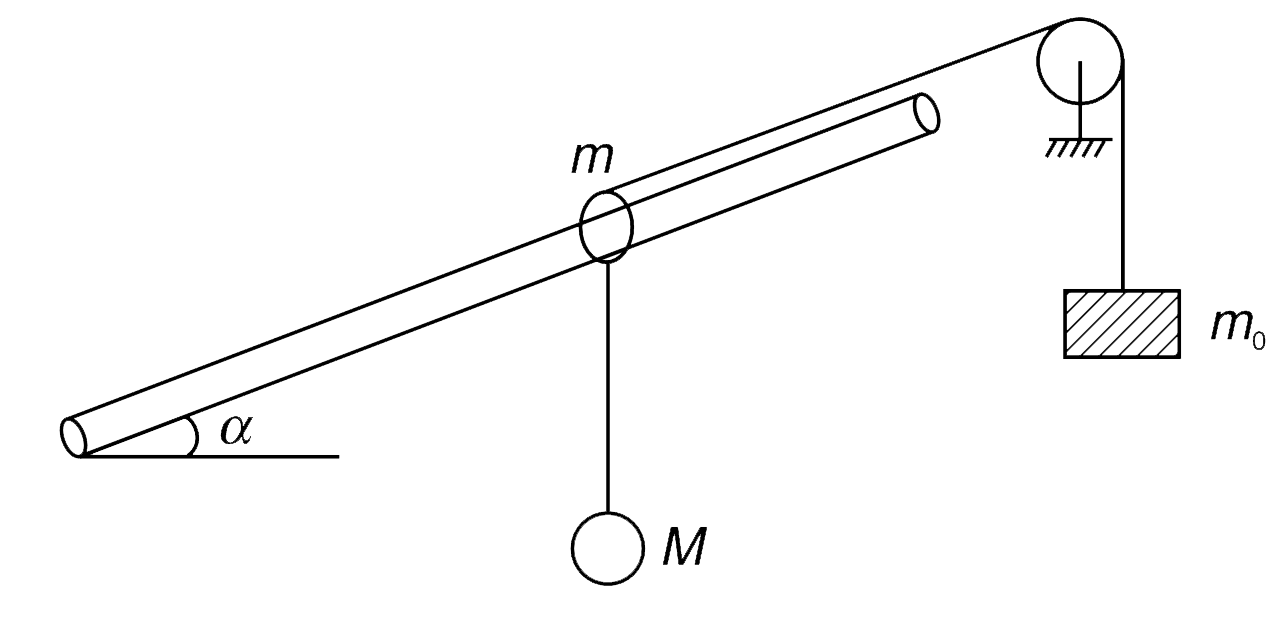
The correct Answer is:(a) (M+m)gsinα
(b) (M+M)gsin2αm+Msin2α
Step by step video, text & image solution for A smooth rod is fixed at an angle alpha to the horizontal. A small ring of mass m can slide along the rod. A thread carrying a small sphere of mass M is attached to the ring. To keep the system in equilibrium, another thread is attached to the ring which carries a load of mass m_(0)at its end (see figure). The thread runs parallel to the rod between the ring and the pulley. All threads and pulley are massless. (a) Find m_(0) so that system is in equilibrium. (b) Find acceleration of the sphere M immediately after the thread supporting m_(0) is cut. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
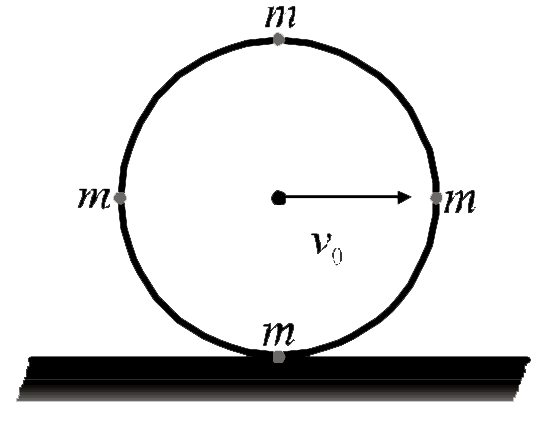
A ring of mass m and radius R has four particles each of mass m attached to the ring as shown in figure. The centre of ring has a speed v0. The kinetic energy of the system is
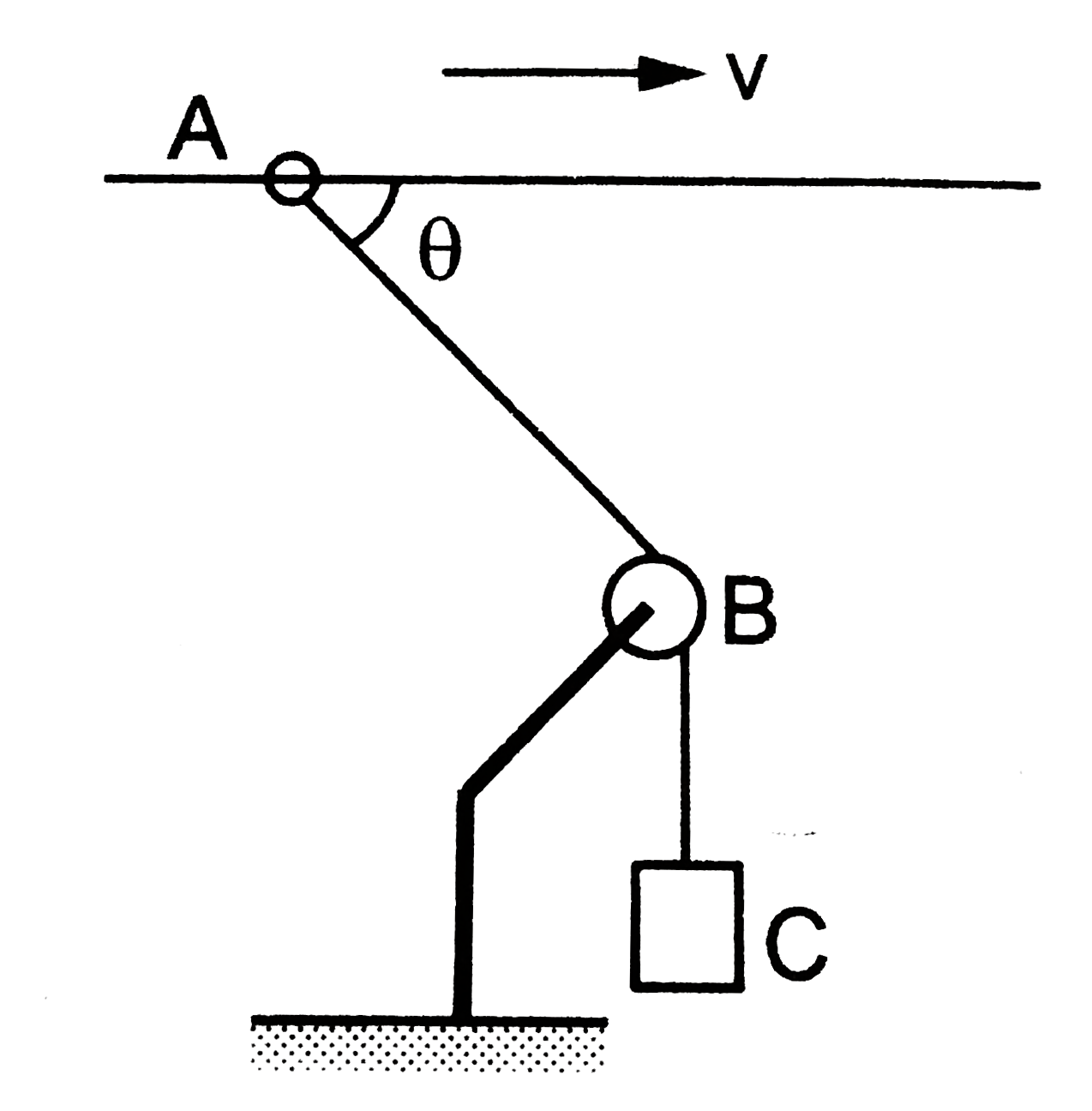
View SolutionA smooth ring A of mass m can slide on a fixed horizontal rod. A string tied to the ring passes over a fixed pulley B and carries a block C of ma M(=2m) as shown in figure. At an instant the string between the ring and the pulley makes an angle θ with the rod. a. Show that, if the ring slides with a pspeed v, the blockdescends with speed vcosθ, b. With whast acceleration will the ring starts moving if the system is released from rest with θ=300
View Solution
Knowledge Check
A smooth ring of mass m can slide on a fixed horizontal rod. A string tied to the ring pases over a fixed pulley B and carries a block C of mass 2m as shown below. As the ring starts sliding
 AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθ
AThe acceleration of the ring is 2gcosθ1+2cos2θBThe acceleration of the block is 2g1+2cos2θCThe tension in the string is 2mg1+2cos2θDIf the block descends with velocity v then the ring slides with velocity vcosθ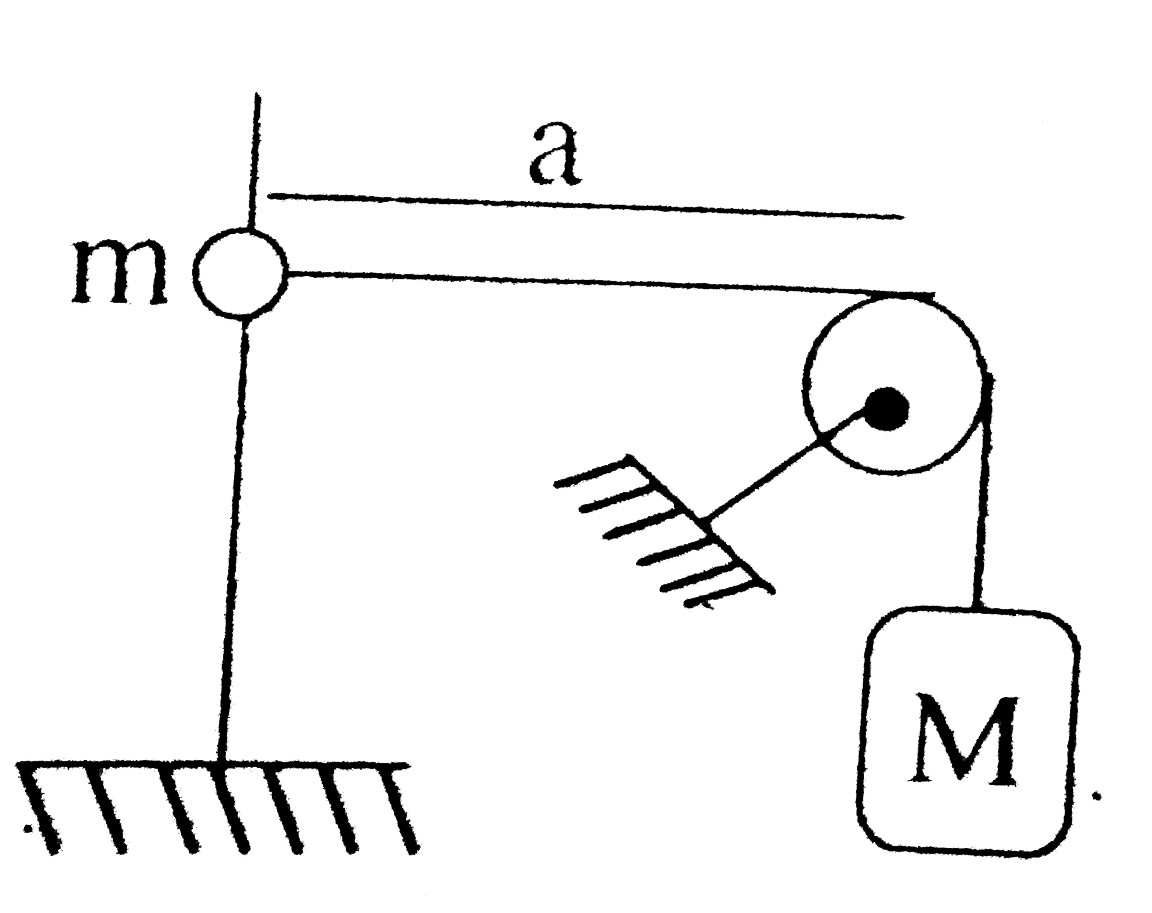
A ring of mass m can slide on the vertical smooth rod. Ring is connected by block with string as shown in figure. Pulley is of mass-less and smooth the system is released from reast. Initial tension in string isAT=MgBT>MgCT<MgDT=Mg+MgA small sphere of mass m suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then
ATotal acceleration of sphere as a function of θ measured from the vertical is g√1+3cos3θBThread tension as a function of θ measured from the vertical is T=3mgcosθCThe angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally is cos−11/√3.DThe thread tension at the moment when the vertical component of the sphere's velocity is maximum will be mg.
A smooth ring A of mass 4 kg can slide on a fixed smooth horizontal rod. A string tied to the ring passes over a fixed pulley and carries a block B of mass 2 kg as shown in the figure. At the initial instant, the string attached to the ring makes an angle 60° with the horizontal rod. If the system is released from rest, the initial acceleration of the ring is?
View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached at its ends. The masses of the pulley and thread are negligible, friction is absent. Find the acceleration of the centre of mass(acm) of this system.
View SolutionA weight of mass m hangs on a thread. The thread is deflected by an angle α0 and let go. Find the tension of the thread as a function of the angle α .
View SolutionA smooth uniform rod of length L and mass M has two identical beads of negligible size each of mass m which can slide freely along the rod. Initially the two beads are at the centre of the rod and the system is rotating with an angular velocity ω0 about an axis perpendicular to the rod and passing through the midpoint of the rod. There are no external forces. When the beads reach the ends of the rod, the angular velocity of the system is ......
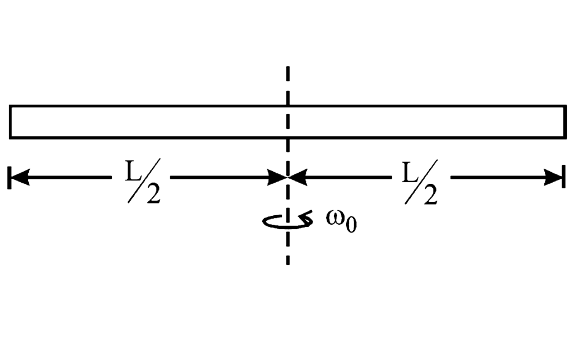
View SolutionA light rod of length l has two masses m1 and m2 attached to its two ends. The moment of inertia of the system about an axis perpendicular to the rod and passing through the centre of mass is.
View Solution
