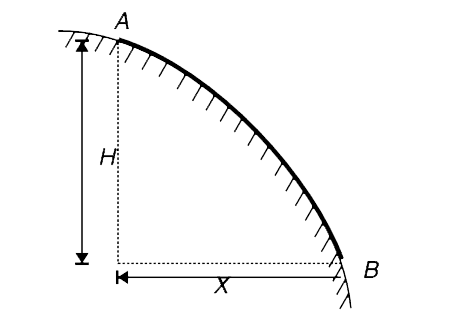
A uniform rope has been placed on a sloping surface as shown in the figure. The vertical separation and horizontal separation between the end points of the rope are H and X respectively. The friction coefficient is just good enough to prevent the rope from sliding down. Find the value of .
The correct Answer is:
Step by step video, text & image solution for A uniform rope has been placed on a sloping surface as shown in the figure. The vertical separation and horizontal separation between the end points of the rope are H and X respectively. The friction coefficient (mu) is just good enough to prevent the rope from sliding down. Find the value of mu. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
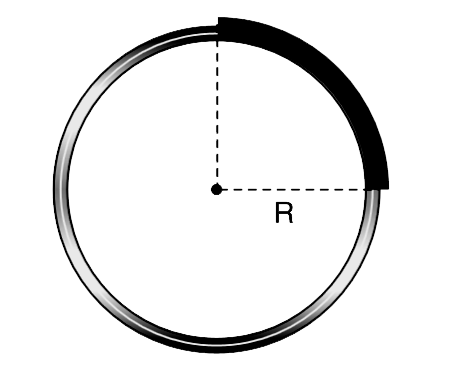
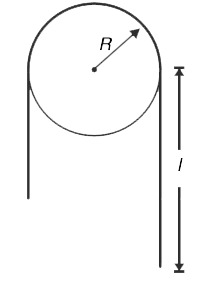
A uniform rope of length πR2 has been placed on fixed cylinder of radius R as shown in the fig. One end of the rope is at the top of the cylinder. The coefficient of friction between the rope and the cylinder is just enough to prevent the rope from sliding. Mass of the rope is M.
(a) At what position, the tension in the rope is maximum?
(b) Calculate the value of maximum tension in the rope.
 View Solution
View SolutionA uniform rope ABCDE has mass M and it is laid along two incline surfaces (AB and CD) and two horizontal surfaces (BC and DE) as shown in figure. The four parts of the rope AB, BC, CD and DE are of equal lengths. The coefficient of friction (μ) is uniform along the entire surface and is just good enough to prevent the rope from sliding.

(a) Find μ
(b) x is distance measured along the length of the rope starting from point A. Plot the variation of tension in the rope (T) with distance x.
(c) Find the maximum tension in the rope.View Solution
Knowledge Check
- Question 1 - Select One
A uniform rope of total length l is at rest on a table with fraction f of its length hanging (see figure). If the coefficient of friction between the table and the chain is μ then
 Af=μBf=1/(1+μ)Cf=1/(1+1/μ)Df=1/(μ+1/μ)
Af=μBf=1/(1+μ)Cf=1/(1+1/μ)Df=1/(μ+1/μ) - Question 2 - Select One or More
In the situration shown in the figure the friction coefficient between M and the horizontal surface is μ. The force F is applied at an angle θ with vertical. The correct statements are
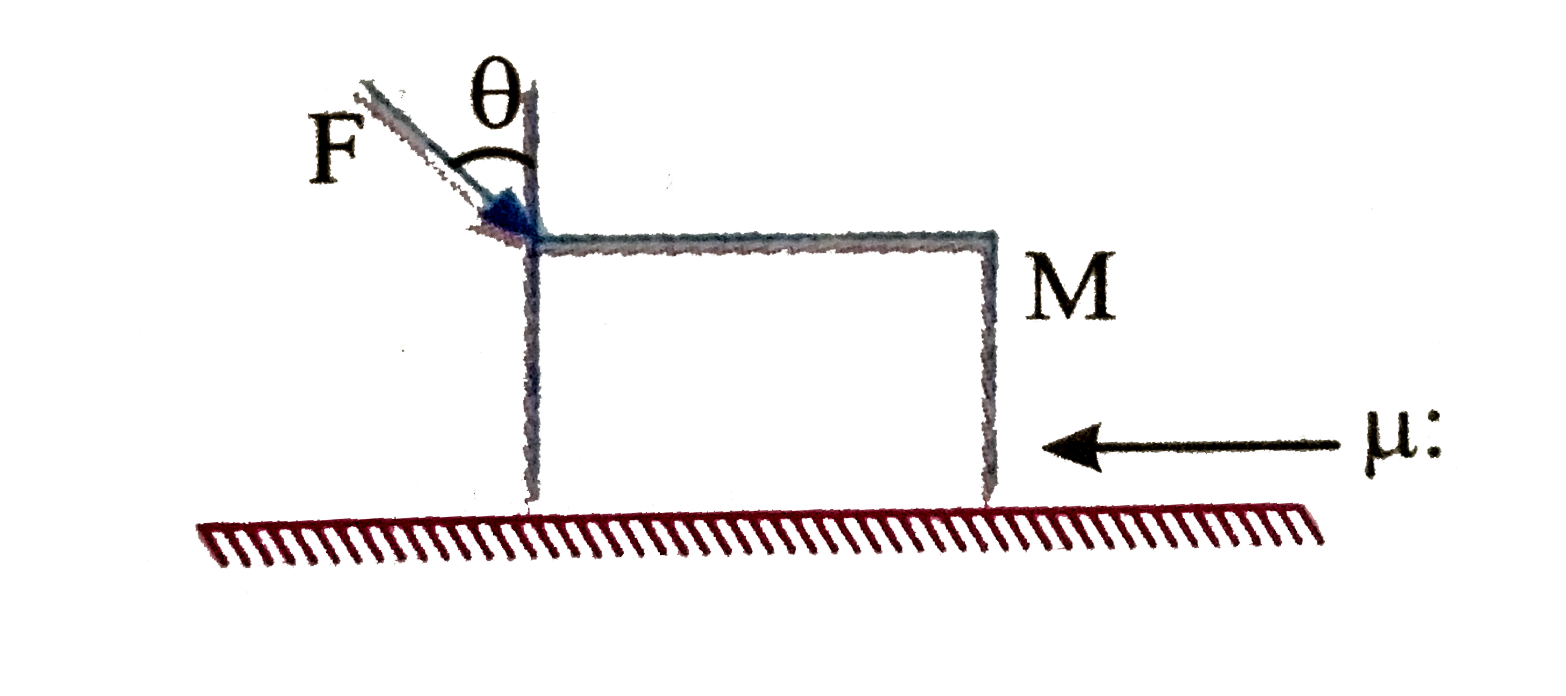 AIf θ>tan−1μ the block cannot be pushed forward for any value of FBIf θ<tan−1μ the block cannot be pushed forwards for any value of FCAs θ decreases the magnitude of force needed to just push the block M forward increasesDNone of these
AIf θ>tan−1μ the block cannot be pushed forward for any value of FBIf θ<tan−1μ the block cannot be pushed forwards for any value of FCAs θ decreases the magnitude of force needed to just push the block M forward increasesDNone of these - Question 3 - Select One
Two block of same mass'm' are joined with an dideal spring of spring constant k and sept on a rough surface as shown in figure. The spring is initially unstretched and coefficient of friction between the blocks and horizontal surface is μ and 2μ respectively. What should be the maximum speed of block 'A' such that the block 'B' does not move ?
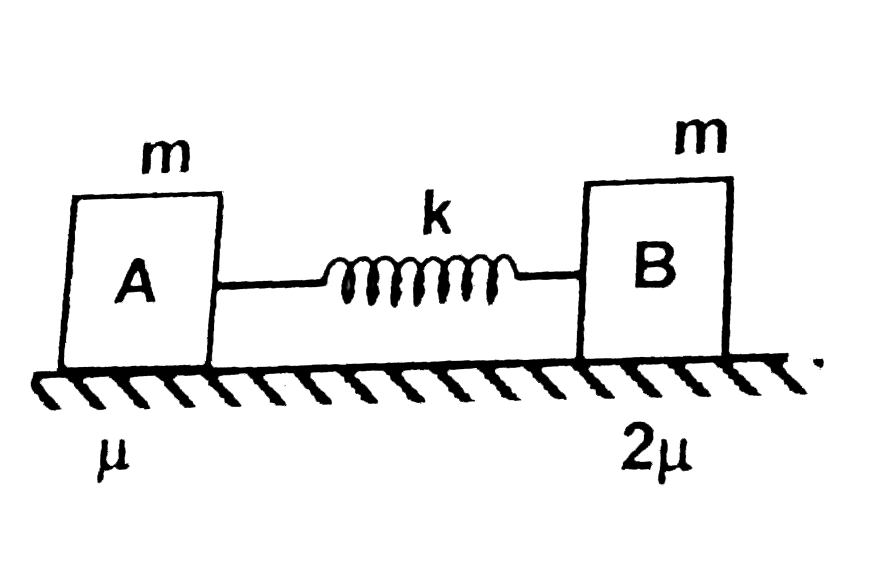 A2μg√2mkBμg√2mkCμg√mkD2μg√m2k
A2μg√2mkBμg√2mkCμg√mkD2μg√m2k
A uniform ring of mass m is placed on a rough horizontal fixed surface as shown in the figure. The coefficient of friction between the left part of the ring and left part of the horizontal surface is μ1=0.6π and between right half and the surface is μ2=0.2π. At the instant shown, now the ring has been imparted an angular velocity in clockwise sense in the figure shown. At this moment magnitude of acceleration of centre O of the ring (in m/s2) is (take g=10m/s2)
 View Solution
View SolutionA uniform rod is placed on two spinning wheels as shown in figure. The axes of the wheels are separated by a distance l=20cm, the coefficient of friction between that in this case the rod performs harmonic oscillations. Find the period of these oscillations.
 View Solution
View SolutionA block lies on a wedge with the slope angle α. The coefficient of static friction between the bar and the wedge is μ<tanα. What should be the acceleration of the wedge to prevent the bar from sliding down?
View SolutionA rope of length L and mass per unit length λ passes over a disc shaped pulley of mass M and radius R. The rope hangs on both sides of the pulley and the length of larger hanging part is l. The pulley can rotate about a horizontal axis passing through its centre. The system is released from rest and it begins to move. The pulley has no friction at its axle and the rope has large enough friction to prevent it from slipping on the pulley.
(a) Find the acceleration of the rope immediately after it is released.
(b) Find the horizontal component of the force applied by the axle on the pulley immediately after the system is released
 View Solution
View SolutionIn the situatiobn shown in the figure the friction coefficient between M and the horizontal surface is μ. The force F is applied at an angle θ with vertical. The correct statements are :
 View Solution
View Solution

