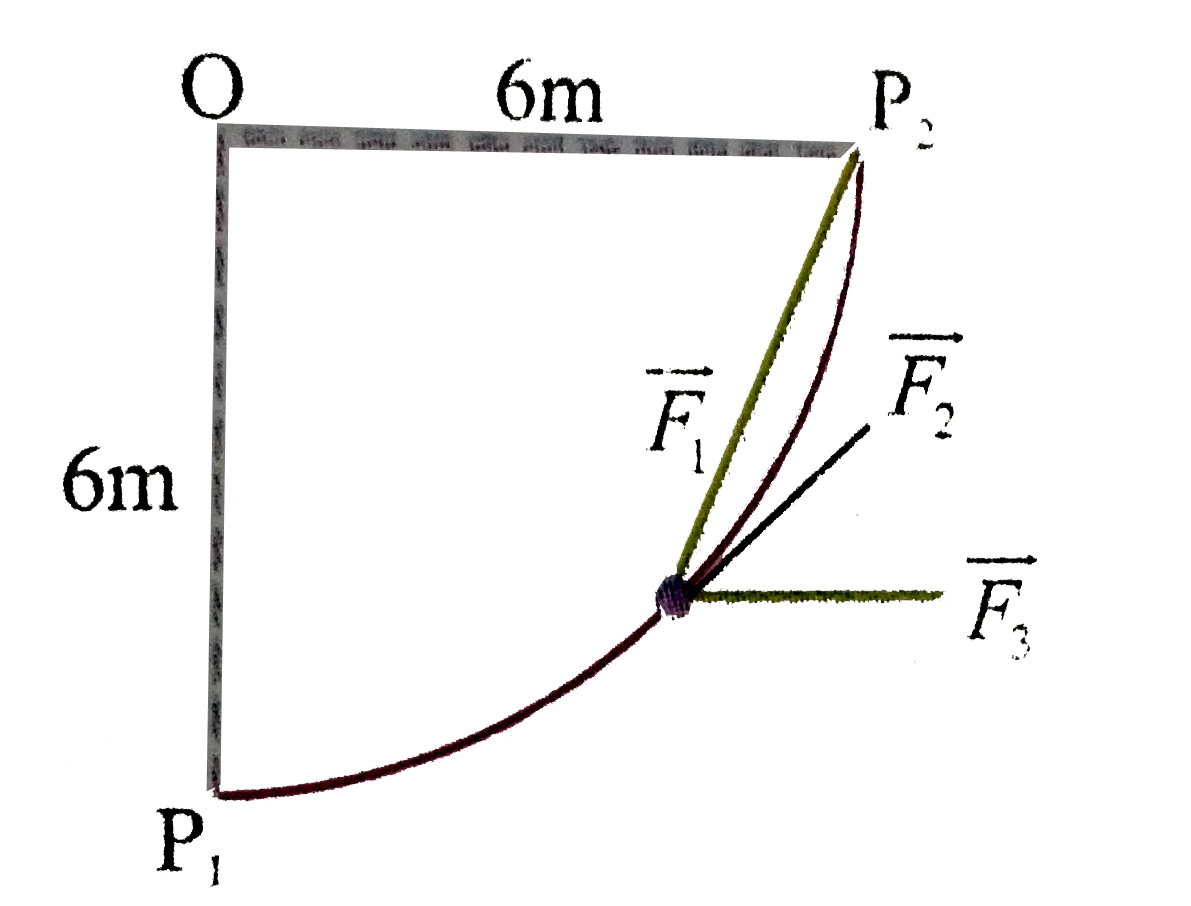
A smooth track in the form of a quarter-circle of radius 6 m lies in the vertical plane. A ring of weight 4(N) moves from P1 and P2 under the action of forces F1,F2 and F3. is always towards P2 under the action of forces F1,F2 and F3 Force F1 is always towards P2 and is always (20) N in maghitude, force F2 always acts hotizontally and is always (30 N) in magnitude, force F3 always acts tangentially to the track and is of magnitude (15−10s)N, where s is in metre. If the particle has speed 4m/s at P1,what will its speed be at P2?
The work done by F(1) is
W1=∫P2P1F1cosθds
From figure, s=R(π2−2θ)
or ds=(6m)d(−2θ)=−12dθ
and F1=20.
At P1, 2θ=π2⇒θ=π4
At, P2,20=0⇒θ=0
Hence,W1=−240∫0π/4cosθdθ
=240sinπ4=120√2J

the work done by F3 is
W3=∫F3ds=∫6(π/2)0(15−10s)ds,(P1P2=Rπ2=6π2)
[15s−5s2]3π0=−302.8J
To calculate the work done by F2 and by w, it is convenient to take the projection of the path in the direction of the force. Thus,
W=(2)F2(OP2)=30(6)=180J
W4=(−w)(P1O)=(−4)(6)=−24J (w=weight)
The total work done is , W1+W3+W2+W4=23J
Then, by the work-energy principle.
KP2−KP1=23J
=12(49.8)v22−12(49.8)(4)2=23.
v2=11.3m/s.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.1
10 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.2
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE2
1 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A block is displaced from (1m,4m,6m) to (2ˆi+3ˆj−4ˆk)m under a constant force F=(6ˆi−2ˆj+ˆk)N. Find the work done by this force.
View SolutionA ball of mass 100 gm is projected upwards with velocity (10m/s). It returns back with (6m/s). Find work done by air resistance .
View SolutionIn the figure sown in the concept, find
(a) Equilbrium extension x∘(=AB)
(b) Maximum extension xm(=AC)
(c)Maximum speed at point B.
View SolutionTwo wires of same material of radii 2r and r are welded together end to end The combination is used as a sonometer wire and is kept under tension T. The welded point lies midway between the bridges. What wil be the ratio of the number of loops formed in the wires, such that the joint is node when the stationary waves are set up in the wire?
View SolutionA body of mass 1kg begins to move under the action of a time dependent force →F=(2tˆI+3t2ˆj)N, where ˆi and ˆj are unit vectors along x-and y-axes. What power will be developed by the force at the time t ?
View SolutionWhen forces F_(1) , F_(2) , F_(3) are acting on a particle of mass m such that F_(2) and F_(3) are mutually prependicular, then the particle remains stationary. If the force F_(1) is now rejmoved then the acceleration of the particle is
View SolutionA body is moving under the action of two force −→F1=2ˆi−5ˆj , −→F2=3ˆi−4ˆj . It's velocity will become uniform under a third force −→F3 given by.
View SolutionA smooth track in the form of a quarter circle of radius 6m lies in the vertical plane. A particle moves from P1 to P2 under the action of forces →F1,→F2 and →F3 Force →F1 is 20N, Force →F2 is always 30N in magnitude. Force →F3 always acts tangentiallly to the track and is of magnitude 15N. Select the correct alternative (s) :
 .
.
View SolutionAB is a quarter of a smooth horizontal circular track of radius R,A particle P of mass m moves along the track from A to B under the action of following forces: vec(F_(1) =F (always towards y-axis) vec(F_(2)) =F (always towards point B) vec(F_(3)) =F (always along the tangent to path AB) vec(F_(4)) =F (always towards x-axis) {:(ColumnI," ",ColumnII),((A) "Work done by" vec(F_(1))," ",(P) sqrt(2)FR),((B) "Work done by" vec(F_(3))," ",(Q)FR),((C) "Work done by" vec(F_(3))," ",(R) (piFR)/(2)),((D) "Work done by" vec(F_(4))," ",(S) (2FR)/(pi)):} Select correct alternative :-
View Solutionबल F1,F2 और F3 एक m द्रव्यमान के कण , पर इस प्रकार कार्य कर रहे हैं कि F1 और F2 परस्पर लंबवत हैं किंतु कण स्थिर रहता है । यदि बल F1 को हटा दिया जाये तो कण का त्वरण होगा -
View SolutionLet fi(x)=sin(2pix) for i=1,2,3&pi∈N. If is given that the fundamental periods of f1(x)+f2(x)+f3(x),f1(x)+f2(x)andf1(x)+f3(x) are π,π3 respectively, then the minimum value of p1+p2+p3 is
View Solutionif P_(1) and P_(2) are two points on the ellipse whose foci are F_(1) and F_(2) then
View SolutionWhen three forces F_(1), F_(2) And F_(3) Is acting on an object of mass m such that F_(2) And F_(3) Is perpendicular, then the object remains in a fixed state. If force F_(1) Will be the acceleration of the object
View SolutionWhen forces F1,F2,F3 are acting on a particle of mass m such that F1 and F2 are mutually perpendicular, then the particle remains stationary, If the force F, is now removed then acceleration of the particle is
View SolutionWhen force F_(1), F_(2), F_(3) are acting on a particle of mass m such that F_(2) and F_(3) are mutually perpendicular, then the particle remains stationary. If the force F_(1) is now removed then acceleration of the particle is
View Solution
