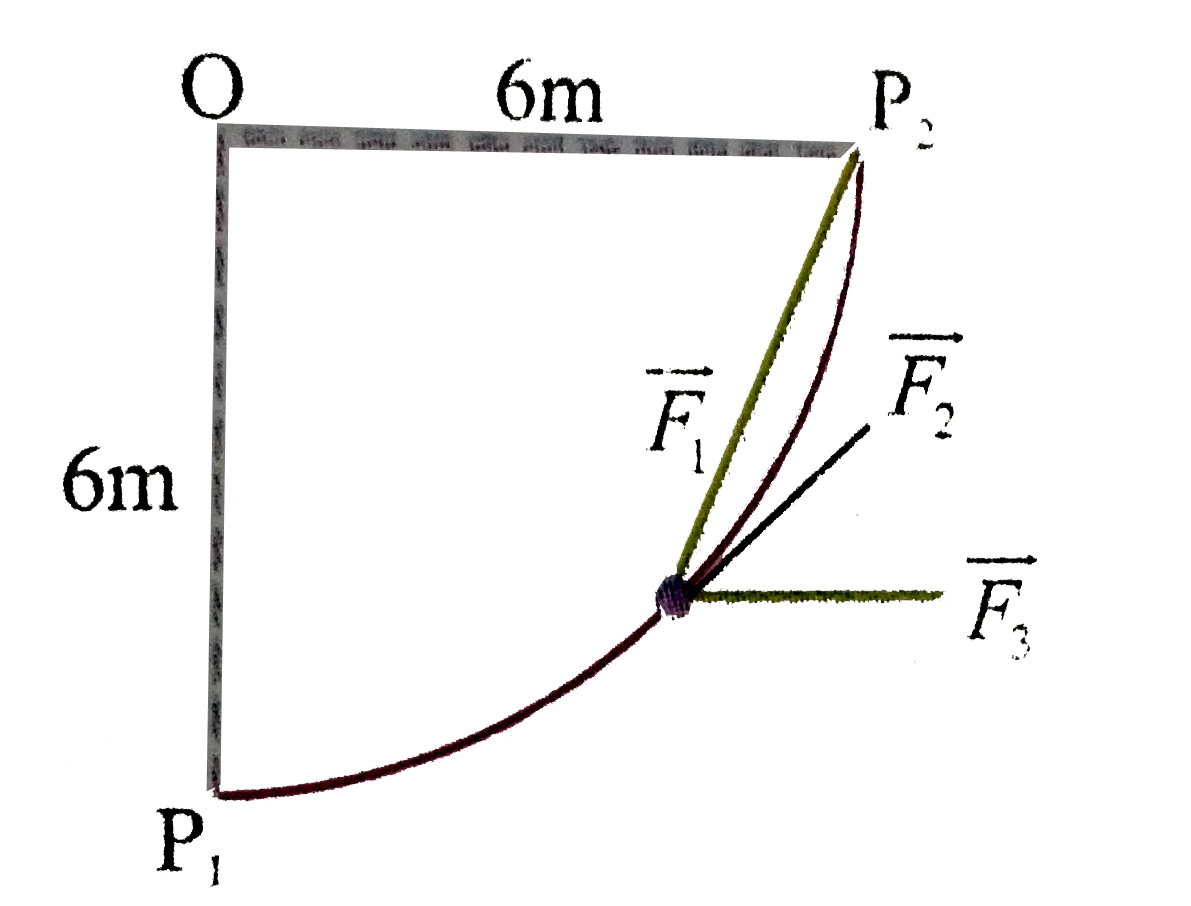
A smooth track in the form of a quarter-circle of radius 6 m lies in the vertical plane. A ring of weight 4(N) moves from P1 and P2 under the action of forces F1,F2 and F3. is always towards P2 under the action of forces F1,F2 and F3 Force F1 is always towards P2 and is always (20) N in maghitude, force F2 always acts hotizontally and is always (30 N) in magnitude, force F3 always acts tangentially to the track and is of magnitude (15−10s)N, where s is in metre. If the particle has speed 4m/s at P1,what will its speed be at P2?
To solve the problem step by step, we will analyze the forces acting on the ring and calculate the work done by each force as the ring moves from point P1 to P2. We will then apply the work-energy principle to find the speed of the ring at P2.
Step 1: Identify the Forces Acting on the Ring
The forces acting on the ring are:
- F1=20N (towards P2)
- F2=30N (horizontal)
- F3=15−10sN (tangential, where s is the distance in meters)
Step 2: Calculate the Work Done by Each Force
1. Work Done by F1:
- The angle between F1 and the displacement ds is 45∘.
- Work done by F1:
W1=F1⋅ds⋅cos(45∘)
- The displacement s from P1 to P2 is the length of the quarter circle:
s=π2⋅r=π2⋅6=3πm
- Thus, the work done by F1:
W1=20⋅3π⋅cos(45∘)=20⋅3π⋅1√2=30√2πJ
2. Work Done by F2:
- Since F2 acts horizontally and does not change the vertical position, the work done is:
W2=F2⋅s=30⋅3π=90πJ
3. Work Done by F3:
- The work done by F3 as the ring moves from P1 to P2:
W3=∫3π0(15−10s)ds
- Evaluating the integral:
W3=(15s−5s2)3π0=15(3π)−5(3π)2=45π−45π2
Step 3: Calculate Total Work Done
- The total work done W is the sum of the work done by all forces:
W=W1+W2+W3
W=30√2π+90π+(45π−45π2)
Step 4: Apply the Work-Energy Principle
- The work-energy principle states:
W=ΔKE=KEf−KEi
- Where:
KEi=12mv2iandKEf=12mv2f
- Given vi=4m/s, we can express the change in kinetic energy:
W=12m(v2f−v2i)
Step 5: Solve for Final Speed vf
- Rearranging gives:
v2f=v2i+2Wm
- Substitute m=4g (where g=9.8m/s2):
v2f=42+2W⋅g4
Step 6: Calculate vf
- Substitute the total work W calculated in step 3 into the equation and solve for vf.
The forces acting on the ring are:
- F1=20N (towards P2)
- F2=30N (horizontal)
- F3=15−10sN (tangential, where s is the distance in meters)
1. Work Done by F1:
- The angle between F1 and the displacement ds is 45∘.
- Work done by F1:
W1=F1⋅ds⋅cos(45∘)
- The displacement s from P1 to P2 is the length of the quarter circle:
s=π2⋅r=π2⋅6=3πm
- Thus, the work done by F1:
W1=20⋅3π⋅cos(45∘)=20⋅3π⋅1√2=30√2πJ
- Since F2 acts horizontally and does not change the vertical position, the work done is:
W2=F2⋅s=30⋅3π=90πJ
- The work done by F3 as the ring moves from P1 to P2:
W3=∫3π0(15−10s)ds
- Evaluating the integral:
W3=(15s−5s2)3π0=15(3π)−5(3π)2=45π−45π2
- The total work done W is the sum of the work done by all forces:
W=W1+W2+W3
W=30√2π+90π+(45π−45π2)
- The work-energy principle states:
W=ΔKE=KEf−KEi
- Where:
KEi=12mv2iandKEf=12mv2f
- Given vi=4m/s, we can express the change in kinetic energy:
W=12m(v2f−v2i)
- Rearranging gives:
v2f=v2i+2Wm
- Substitute m=4g (where g=9.8m/s2):
v2f=42+2W⋅g4
- Substitute the total work W calculated in step 3 into the equation and solve for vf.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.1
10 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.2
9 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - TYPE2
1 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
A smooth track is in the form of a quarter circle of radius 10 m lies in the vertical plane. A bead moves from A and B along the circular track under the action of forces →F1,→F2 and →F3 Force →F1 acts always towards point B and is always 20 N in magnitude Force →F2 always acts horizontally and is always 25 N in magnitude. Force →F3 always acts tangentially to the track and is of constant magnitude 10 N. Select the correct answer.

View SolutionA smooth track in the form of a quarter circle of radius 6m lies in the vertical plane. A particle moves from P1 to P2 under the action of forces →F1,→F2 and →F3 Force →F1 is always 30N in magnitude. Force →F3 always acts tangentiallly to the track and is of magnitude 15N. Select the correct alternative (s) :
 .
.
View Solution
Knowledge Check
A body is moving under the action of two force −−−−−−−−−−→F1=2ˆi−5ˆj , −−−−−−−−−−→F2=3ˆi−4ˆj . Its velocity will become uniform under a third force −→F3 given by.
A5ˆi−9ˆjB−5ˆi−9ˆjC5ˆi+9ˆjD−5ˆi+9ˆjA body is moving under the action of two force −−−−−−−−−−→F1=2ˆi−5ˆj , −−−−−−−−−−→F2=3ˆi−4ˆj . Its velocity will become uniform under a third force −→F3 given by.
A5ˆi−ˆjB−5ˆi−ˆjC5ˆi+ˆjD−5ˆi+9ˆj
A particle moves from point P(1,2,3) to (2,1,4) under the action of a constant force F=(2ˆi+ˆj+ˆk)N. Work done by the force is
View SolutionA particle moves from point P(1,2,3) to (2,1,4) under the action of a constant force F=(2ˆi+ˆj+ˆk)N. Work done by the force is
View SolutionTwo forces F1 and F2 are acting on a rod abc as shown in figure.

View SolutionAB is a quarter of smooth circular track of radius R=6m. A particle P of mass 0.5kg moves along the track from A to B under the action of the following forces.
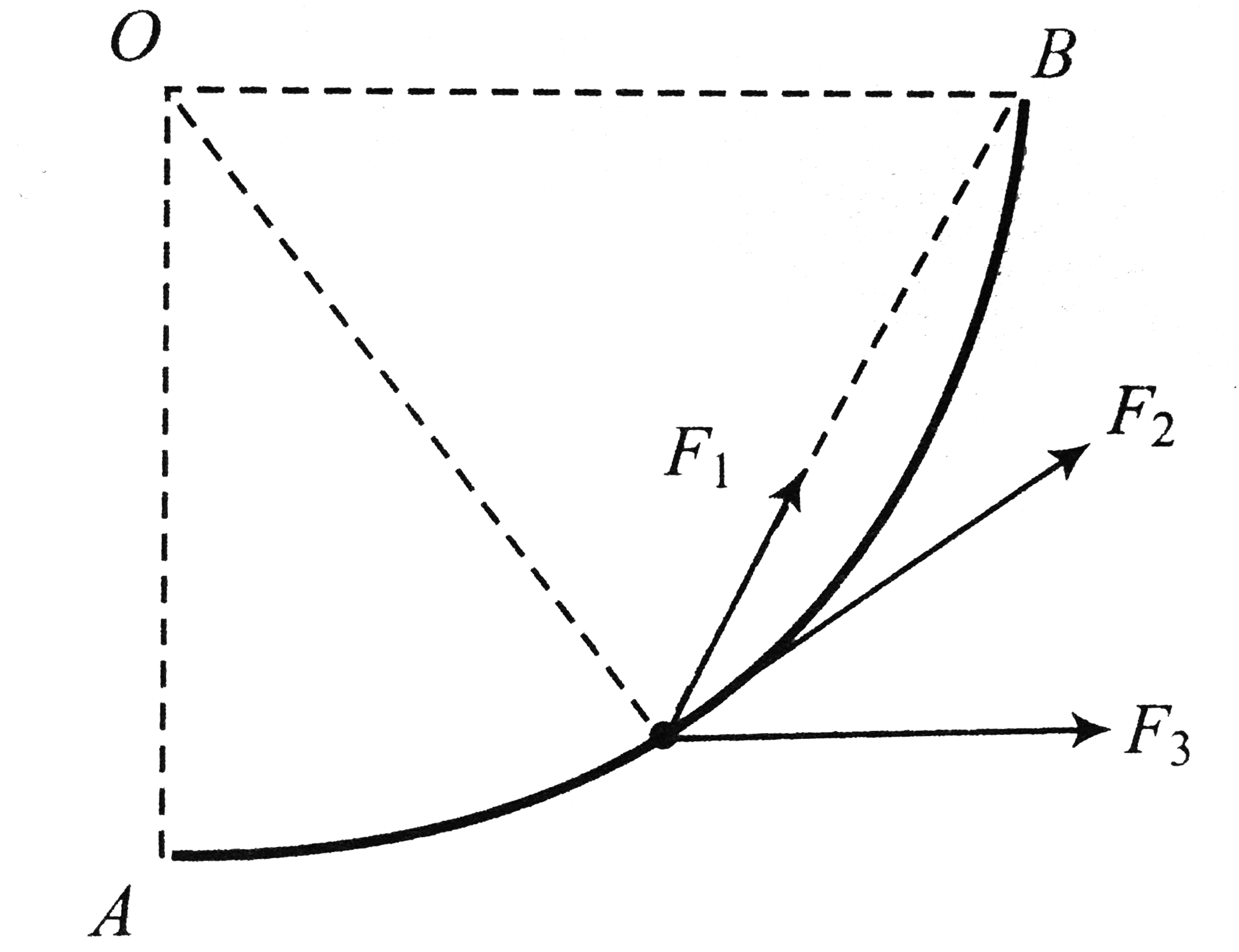
a. A force F1 directed always towards the point B, its magnitude is constant and is equal to 20N.
b. A force F2 directed along the instantaneous tangent to the circular track, its magnitude is (15−10S)N, where S is the distance travelled in metre.
c. A horizontal force of magnitude 30N.
Find the work done by forces mentioned in (a), (b) and (c)
View SolutionTwo forces of mangitude F1 and F2 are acting on an object.The magnitude of the net force Fnet on the object will be in the range.
View SolutionLet us consider two forces F1 and F2 acting on a body of mass 2 kg as shown in the figure. F1=10N, F2=2N , what will be the acceleration?

View Solution
