A smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?

Method 1 (Ground frame method)
At the maximum height, both m1 and m2 have same velocity as the relative sliding between them stops. Since no external force acts horizontally, linear momentum is conserved in horizontal direction
(→px)f=(→px)i
where →pxi=m1v0ˆi and →pxf=(m1+m2)vˆi
Then we have (m1+m2)v=m1v0
WE theorem Wext+Wint=△K
where Wext=−m1gh,Wint=Wcontact=0,
and △K=[12(m1+m2)v2−m1v202]
This gives −m1gh=12(m1+m2)v2−m1v202........ii
Sustituting v from eqn i and eqn ii we have
h=v202(1+m1m2)g
Method 2: (Work energy theorem from centre of mass frame)
The block attains a maximum height when the final relative velociyt vrel between block and wedge becomes zero.
that mean (vref)=0.
The initial relative velocity betwen block and wedge is given as
(vref)i=v0
Substituting (vref_(f)=0 and (vrel)i=v0 in the formula.
△K'=12μ[(vrel_(f)2−(vrel)2i]
we have △K'=−12μv20
while ascending through a height h (say) the external force, that is the earth's gravity does work on the block m1 which can be given as:
Wext(=Wgravity)=−m1gh
The internal (constraint) forces (normal reactions) between m1 and m2 as a whole do not performe work, W∫=0
Finally, putting △K'=−12μv20,Wext=−m1gh and Wint=0 in
We theorem Wext+Wint=△K'
we have −m1gh+0=−12μv20
whereμ=m1m1m1+m2
This gives h=v202(1+m1m2)g
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Solved Examples13videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.120videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICSCHAPTER - CALORIMETRYEXERCISE - Solved Example13videos
CALORIMETRY
- BOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
Similar Questions
Figure shows a block A of mass 6m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
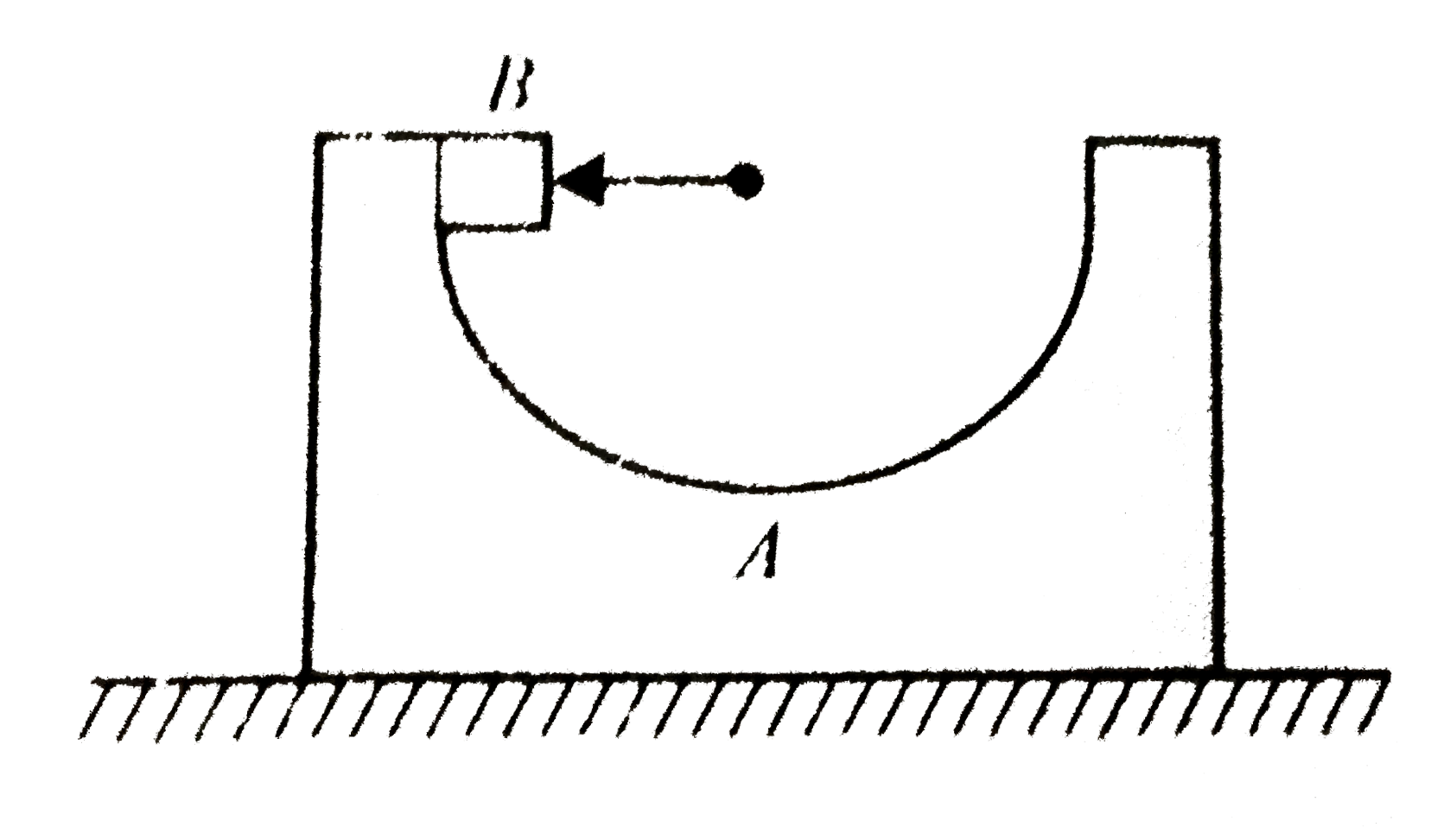 View Solution
View SolutionA body of mass M with a small block m placed on it rests on a smooth horizontal surface. The block is set in motion in the horizontal direction with a velocity v. To what height relative to the initial level will the block rise after breaking off from the body M. Friction can be assumed to be absent.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
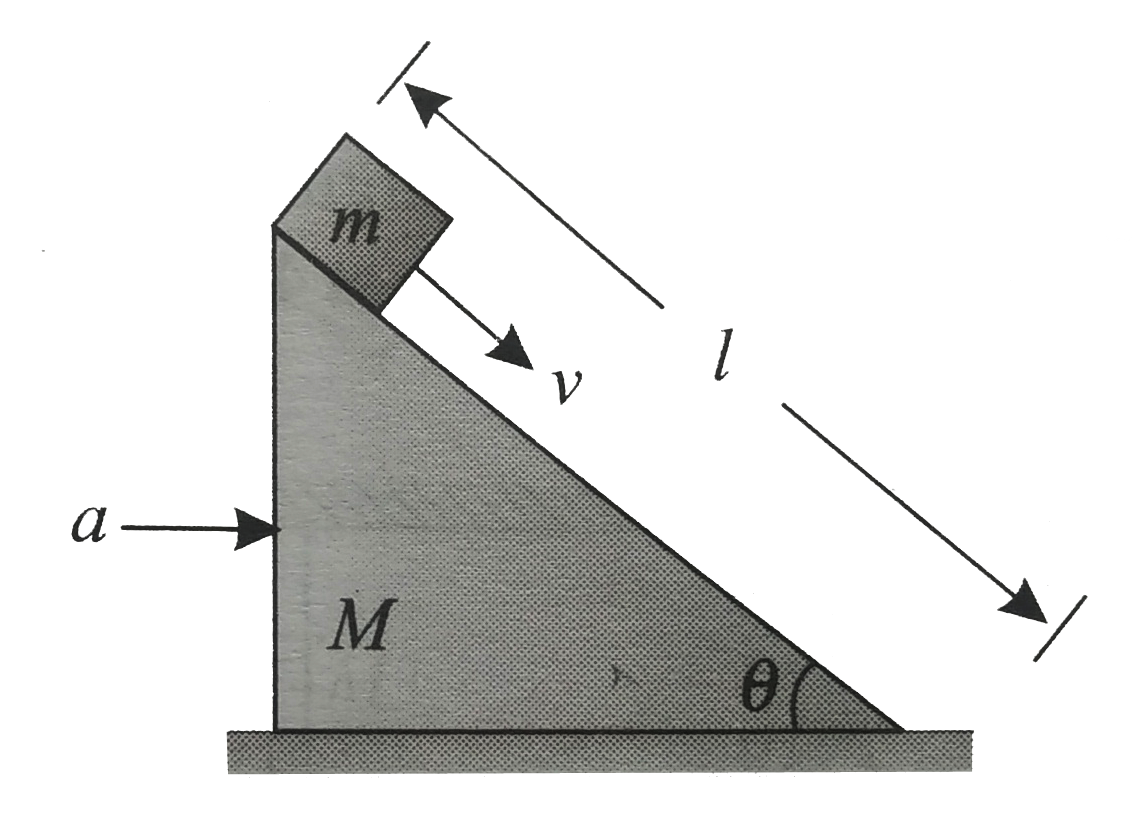
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
Q. The time taken by the block to reach the ground is:AlvB√2lgsinθC√2lgcosθDvgsinθ - Question 2 - Select One
_2019_CBT4_E01_069_Q01.png)
A wedge of mass 4m is initially at rest on frictionles horizotnal surface. A small block of mass m moving with speed v0 and climbs on wedge. Find maximum height achieved by blockA5v202gB25v20gCv202gD2v20g - Question 3 - Select One
A long block A of mass M is at rest on a smooth horizontal surface.A small block B of mass M/2 is placed on A at one end and projected along A with some veklocity v.The coefficient of friction between the block is μ then , the accelerations of blocks A and B before reaching a common velocity will be respectively
 Aμg2(towards right),μg2(towards left)Bμg2(towards right),(μg)(towrards left)Cμg2(towards right),(μg)(towrards left)D(μg)(towards right),μg2(towrards left)
Aμg2(towards right),μg2(towards left)Bμg2(towards right),(μg)(towrards left)Cμg2(towards right),(μg)(towrards left)D(μg)(towards right),μg2(towrards left)
A wedge of mass m1 with its upper surface hemispherical in shape, as shown in Fig. 4E. 7 (a), rests on a smooth horizontal. surface near thewall. A small block of mass m2 slides without friction on the hemispherical surface of the wedge. What is the 'maxi.mum velocity attained by the wedge ?
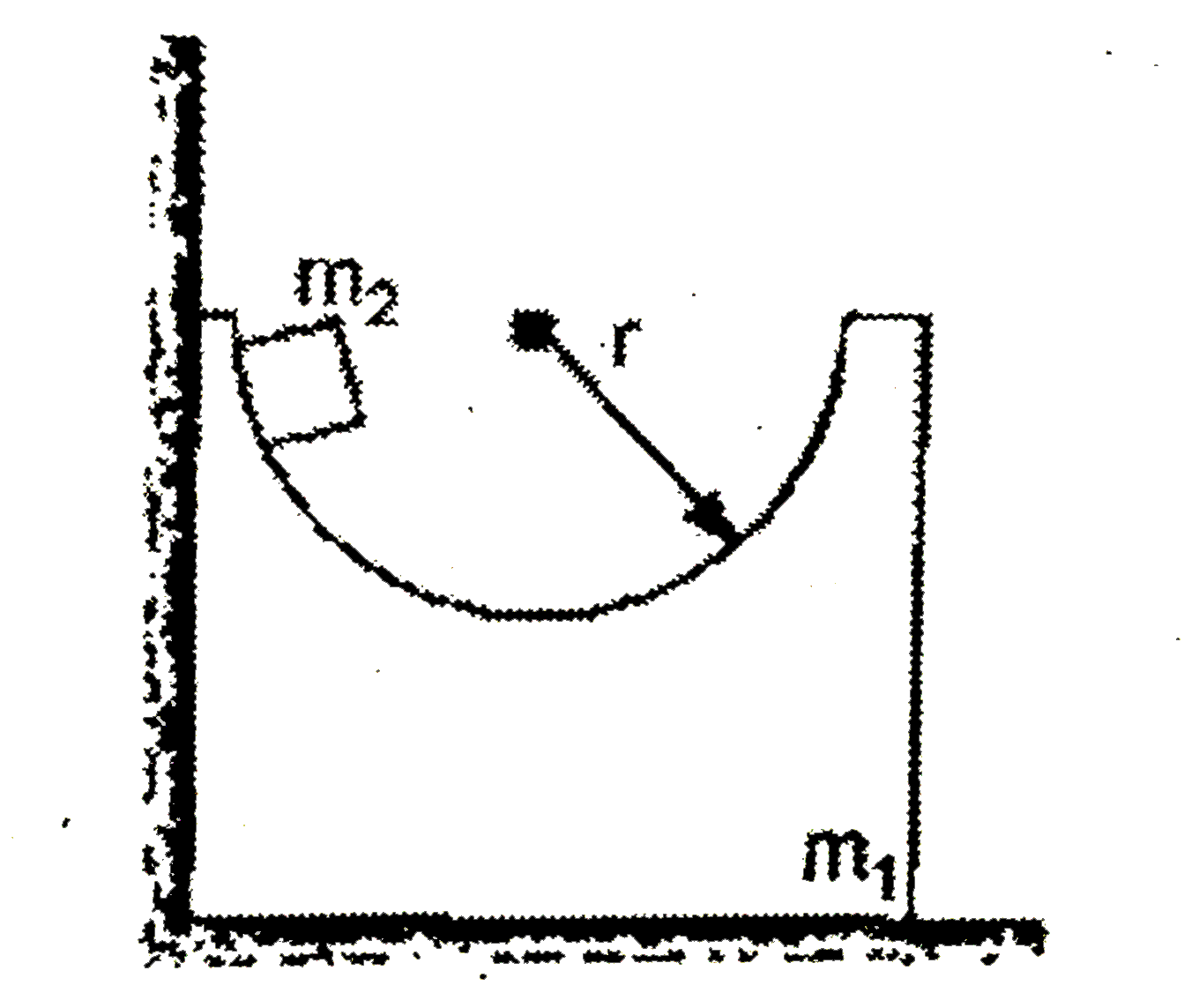 View Solution
View SolutionThe inclined surfaces of two movable wedges of the same mass M are smoothly conjugated with the horizontal plane as shown in figure. A.small block of mass m slides down the left wedge from a height h. To what maximum, height will the block rises on the right wedge.
 View Solution
View Solution
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
The horizontal force applied on the wedge is:View Solution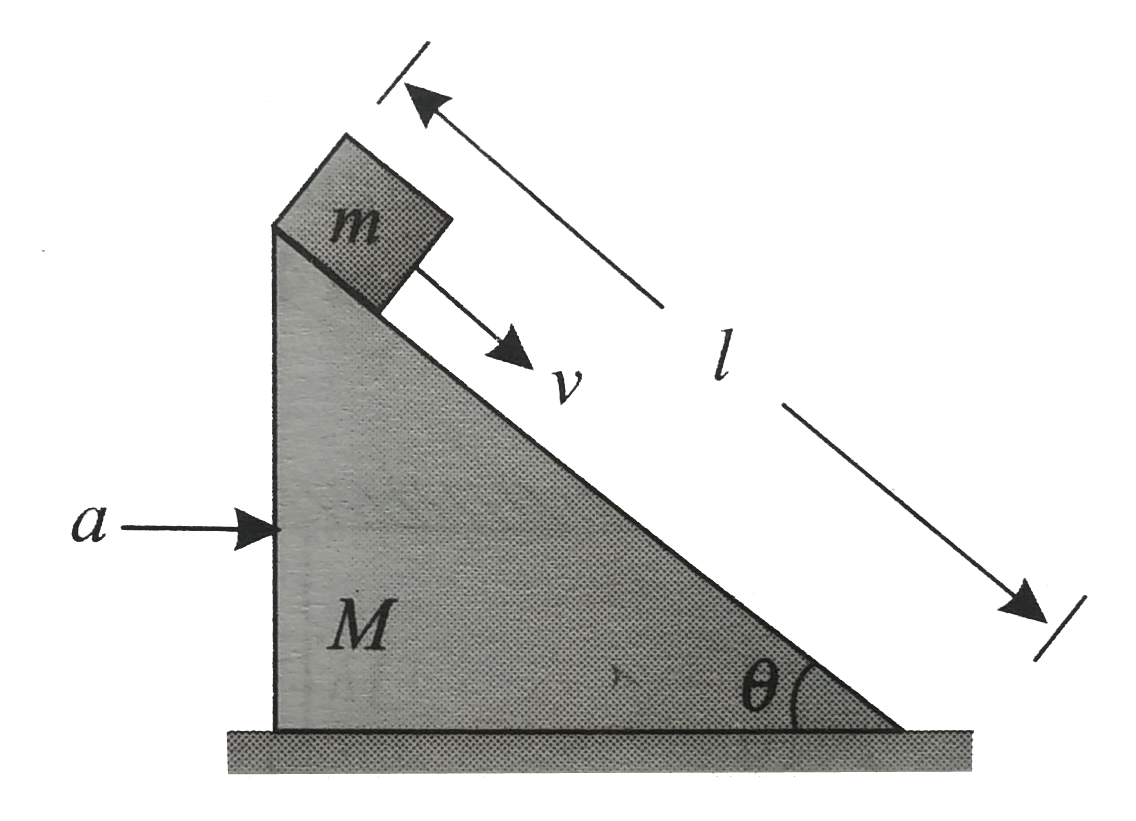
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
Q. The normal reaction between wedge and block is:View Solution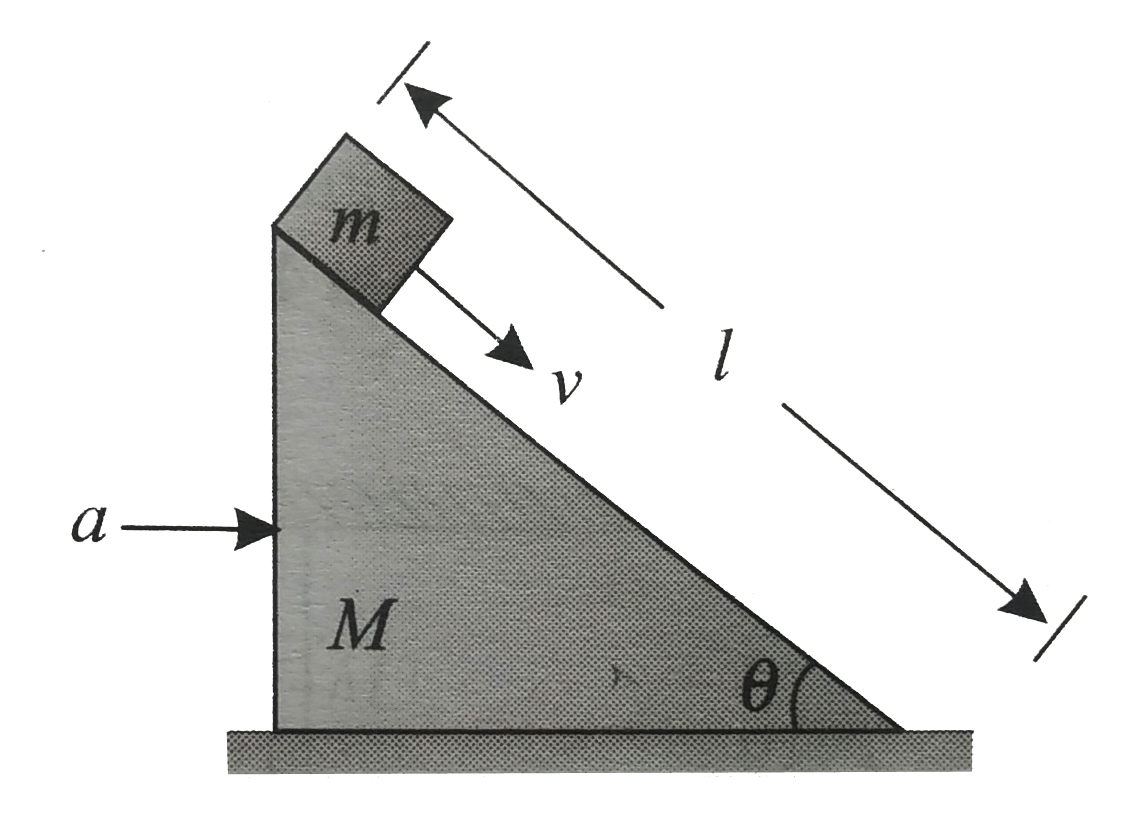
A smooth wedge of mass M is pushed with an acceleration a=>anθ and a block of mass m is projected down the slant with a velocity v relative to the wedge.
Q. The normal reaction offered by ground to the wedge is:View Solution

