A body of mass M with a small block m placed on it rests on a smooth horizontal surface. The block is set in motion in the horizontal direction with a velocity v. To what height relative to the initial level will the block rise after breaking off from the body M. Friction can be assumed to be absent.

The correct Answer is:Mv22(M+m)g
Just at the time of breaking off, let m move with vx in horizontal and vy in vertical direction. At the instant M will also be moving with v=vx in horizontal direction.

Applying COM along x-axis
mv=(m+M)vx⇒vx=(mm+M)v ..........(i)
Apply COE
12mv2=12m(v2x+v2y)+12Mv2y+mgh1 .....(ii)
After breaking off M, moves in projectile
v2y=2gh2⇒mgh2−12mv2y=0 ...(iii)
From (ii) & (iii)
12mv2=12mv2x+12Mv2x+mg(h1+h2)
⇒2ms(h1+h2)=[mv2−mv2x−Mv2x]
⇒h1+h2=Mv22(m+M)g
Topper's Solved these Questions
- BOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-I (H.W)52videos
COLLISION
- BOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Level-II (H.W)54videos
COLLISION
- BOOK - NARAYNACHAPTER - COLLISIONEXERCISE - Comprehension type35videos
COLLISION
- BOOK - NARAYNACHAPTER - CIRCULAR MOTIONEXERCISE - LEVEL II(H.W)51videos
CIRCULAR MOTION
- BOOK - NARAYNACHAPTER - FRICTIONEXERCISE - Passage type of questions I6videos
FRICTION
Similar Questions
A body of mass M (figure) with a small disc of mass m placed on it rests on a smooth horizontal plane. The disc is set in motion in the horizontal direction with velocity v. To what height (relative to the initial level) will the disc rise after breaking off the body M? The friction is assumed to be absent.
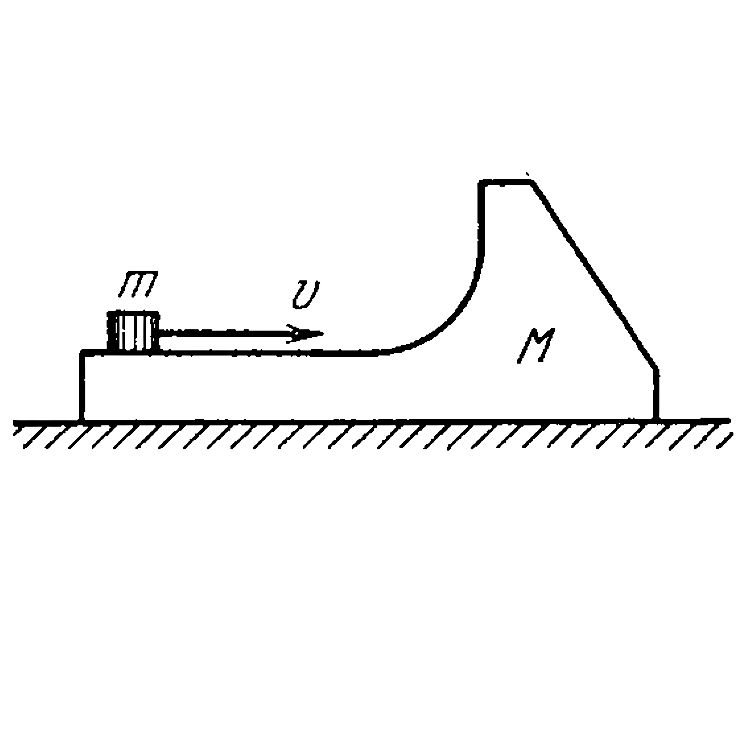 View Solution
View SolutionA body of mass M with a small box of mass m placed on it rests on a smooth horizontal surface. The box is set in motion in the horizontal direction with a velocity u as shown in figure. To what height relative to the initial level will the box rise after breaking off from the body M? Assume all surfaces are frictionless.
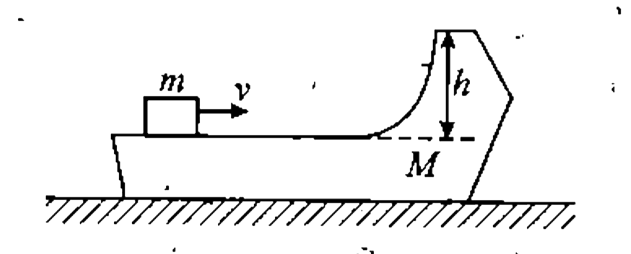 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A long block A is at rest on a smooth horizontal surface. A small block B, whose mass is half of A, is placed on A at one end and projected along A with some velocity u. The coefficient of friction between the blocks is μ:
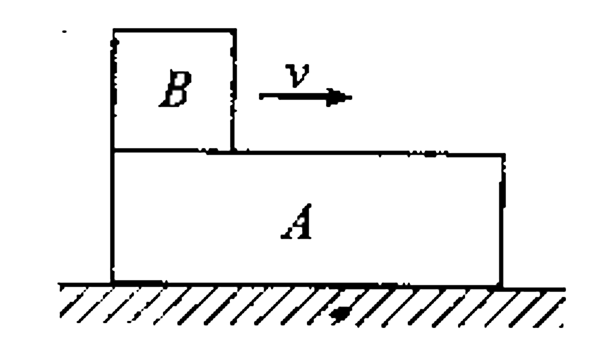 AThe blocks will reach the final common velocity u3Bthe work done against friction is two-thirds of the initial kinetic energy of BCbefore the block reach a common velocity the acceleration of A relative to B is 23μg.DBefore the blocks reach a common velocity the acceleration of A relative to B is 32μg.
AThe blocks will reach the final common velocity u3Bthe work done against friction is two-thirds of the initial kinetic energy of BCbefore the block reach a common velocity the acceleration of A relative to B is 23μg.DBefore the blocks reach a common velocity the acceleration of A relative to B is 32μg. - Question 2 - Select One
A block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
A12B√3C1√3DNone - Question 3 - Select One or More
A block of mass m moves on a horizontal rough surface with initial velocity v. The height of the centre of mass of the block is h from the surface. Consider a point A on the surface.
Aangular momentum about A is mvh initiallyBthe velocity of the block decreases at time passes.Ctorque of the forces acting on block is zero about ADangular momentum is not conserved about A.
A smooth wedge of mass M rests on a smooth horizontal surface. A block of mass m is projected from its lowermost point with velocity v0. What is the maximum height reached by the block?
 View Solution
View SolutionA block of mass m is placed at rest on a smooth wedge of mass M placed at rest on a smooth horizontal surface. As the system is released
 View Solution
View Solution48.A block of mass 5kg is at rest on a smooth horizontal surface Water coming out of a pipe horizontally at the rate of 2kg/sec ,hits the block with a velocity of 6m/sec.The initial acceleration of the block is
View SolutionA block of mass m is placed at rest on a horizontal rought surface with angle of friction ϕ. The block is pulley with a force F at an angle θ with the horizontal. The minimum value of F required to move the block is
View SolutionA block of mass M is resting on a smooth horizontal plane. One end of a uniform rope of mass M4 is fixed to the block , which pulled it in the horizontal direction by applying a force F at the other ends . The tension in the middle of the rope is
View Solution

