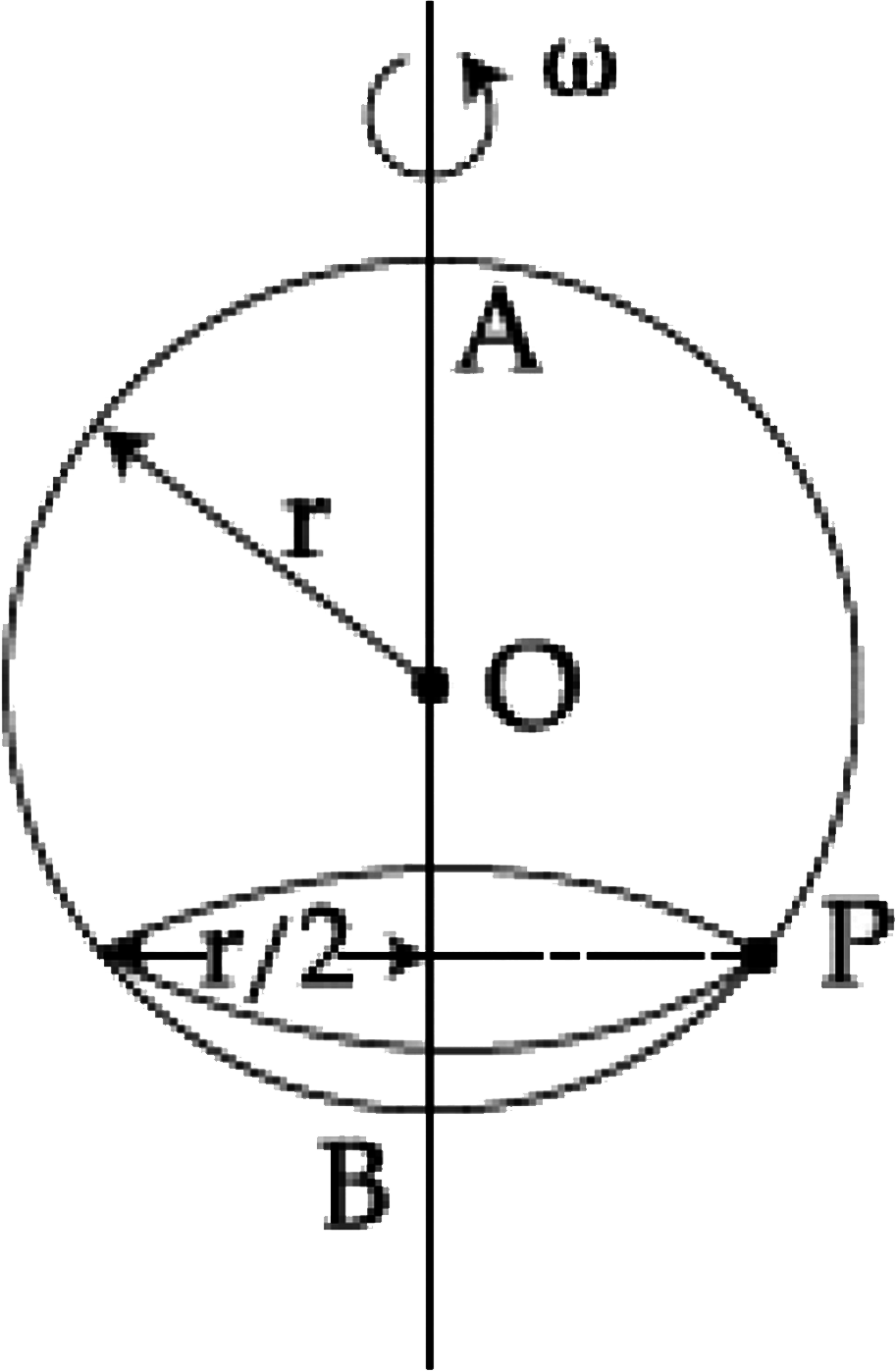
A smooth wire of length 2πr is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed ω about the vertical diameter AB, as shown in figure, the bead is at rest with respect to the circular ring at position P as shown. then the value of ω2 is equal to :
 .
.
2ga
g2a
2ga√3
g√32a
The correct Answer is:c

N=cosθ=mg…(i)
Nsinθ=mω2a2…(ii)
from eqs(ii)(i),tanθ=ω2a2g⇒ω2=2gtanθa
Nowsinθ=a2×1aorθ=30∘
orω2=2g√3a
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Multiple Correct
2 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Linked Comprehension
52 Videos
- NEWTON'S LAWS OF MOTION 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 2EXERCISE - Subjective
21 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
Similar Questions
A smooth wire of length 2πr is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed about the vertical diameter AB, as shown in the figure, the bead is at rest with respect to the circular ring at potion P as shown. Then the value of ω2 is equal to:
View SolutionA smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is ar rest w.r.t. the circular ring in the position shown. then ω2 is equal to:

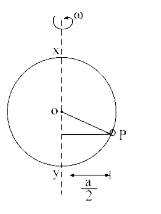
View SolutionA small ring P is threaded on a smooth wire bent in the form of a circle of radius a and centre O. The wire is rotating with constant angular speed ω about a vertical diameter xy, while the ring remains at rest relative to the wire at a distance a2 from xy. Then ω2 is equal to:
View SolutionA rod of length l is rotating with an angular speed ω about its one end which is at a distance a from an infinitely long wire carrying current i.Find the emf induced in the rod at the instant shown in the figure.

View Solution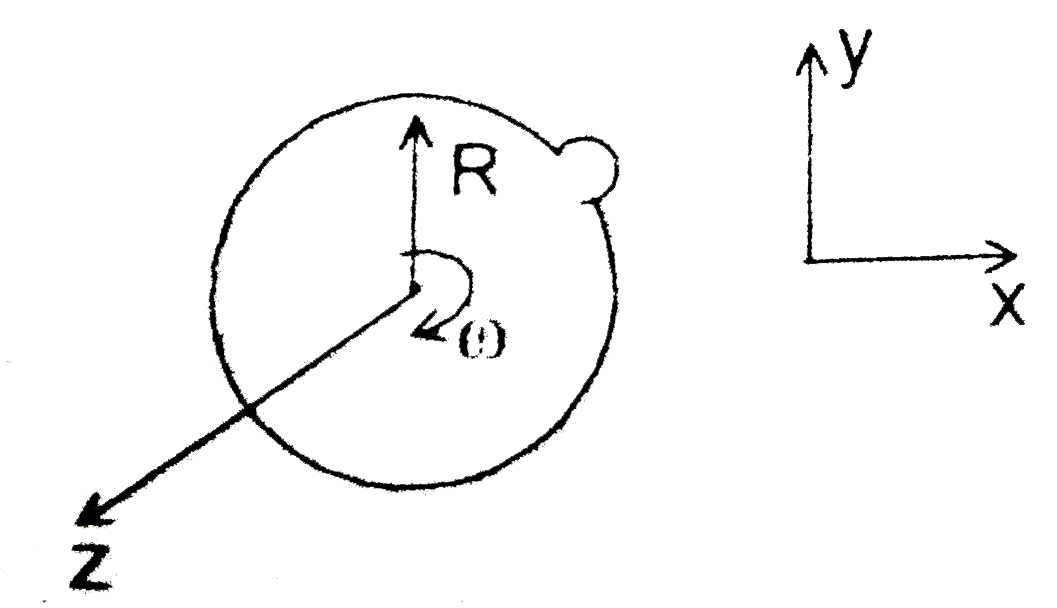
A small pulse is generated on a ring rotating with constant angular velocity ω as shown in the figure. Then the speed of pulse with respect to ground.
View SolutionA rod of length l is rotating with an angular speed ω about one of its ends which is at a distance a from an infinitely long wire carrying current i. Find the emf induecd in the rod at the instanr shown in .
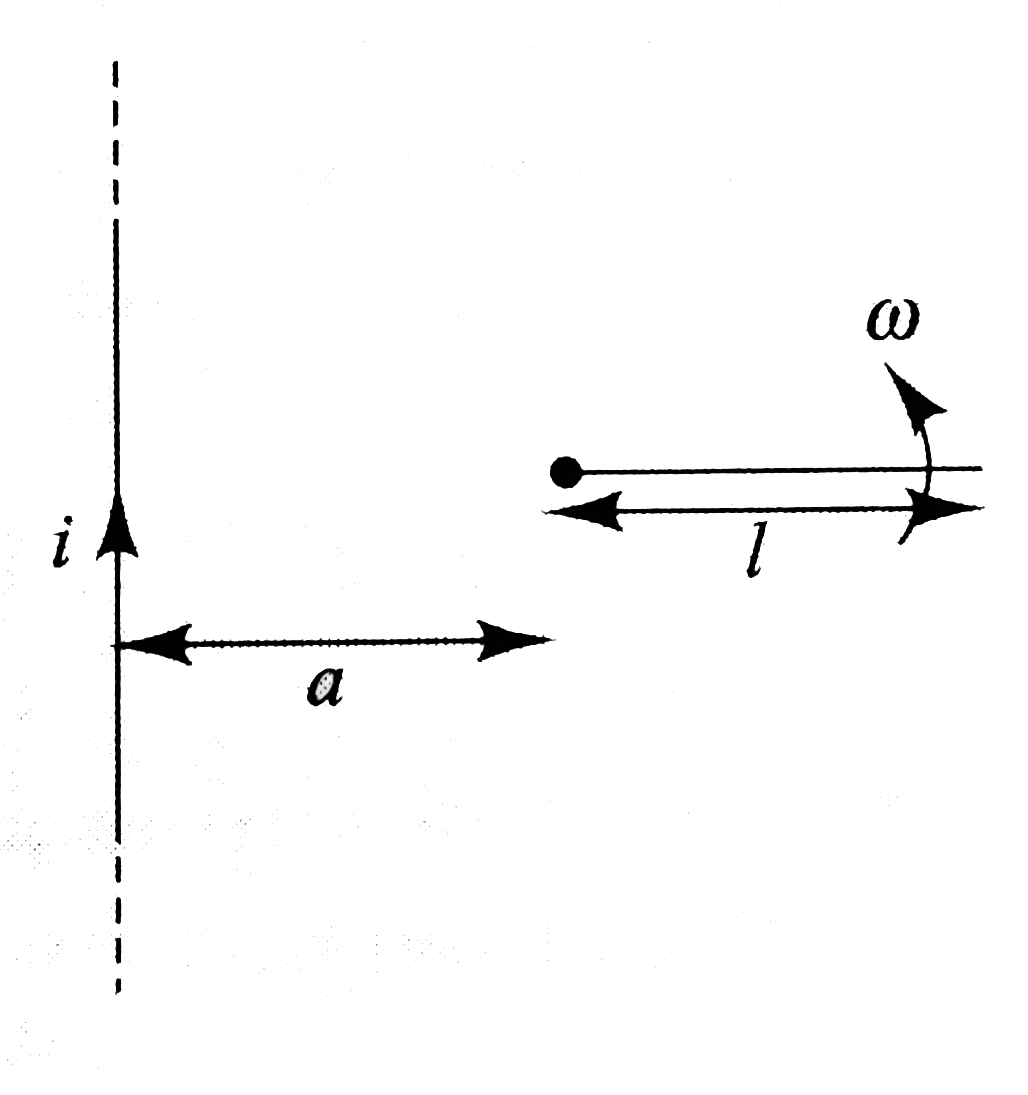
View SolutionA wire of resistance 4Ω is bent to form a circle. The resistance point A and B will be
_PHY_E05_303_Q01.png)
View SolutionA rod of length l is rotating with an angular speed ω about one of its ends which is at a distance a from an infinitely lonf wire carrying current i. Find the emf induced in the rod at the instant shown in .
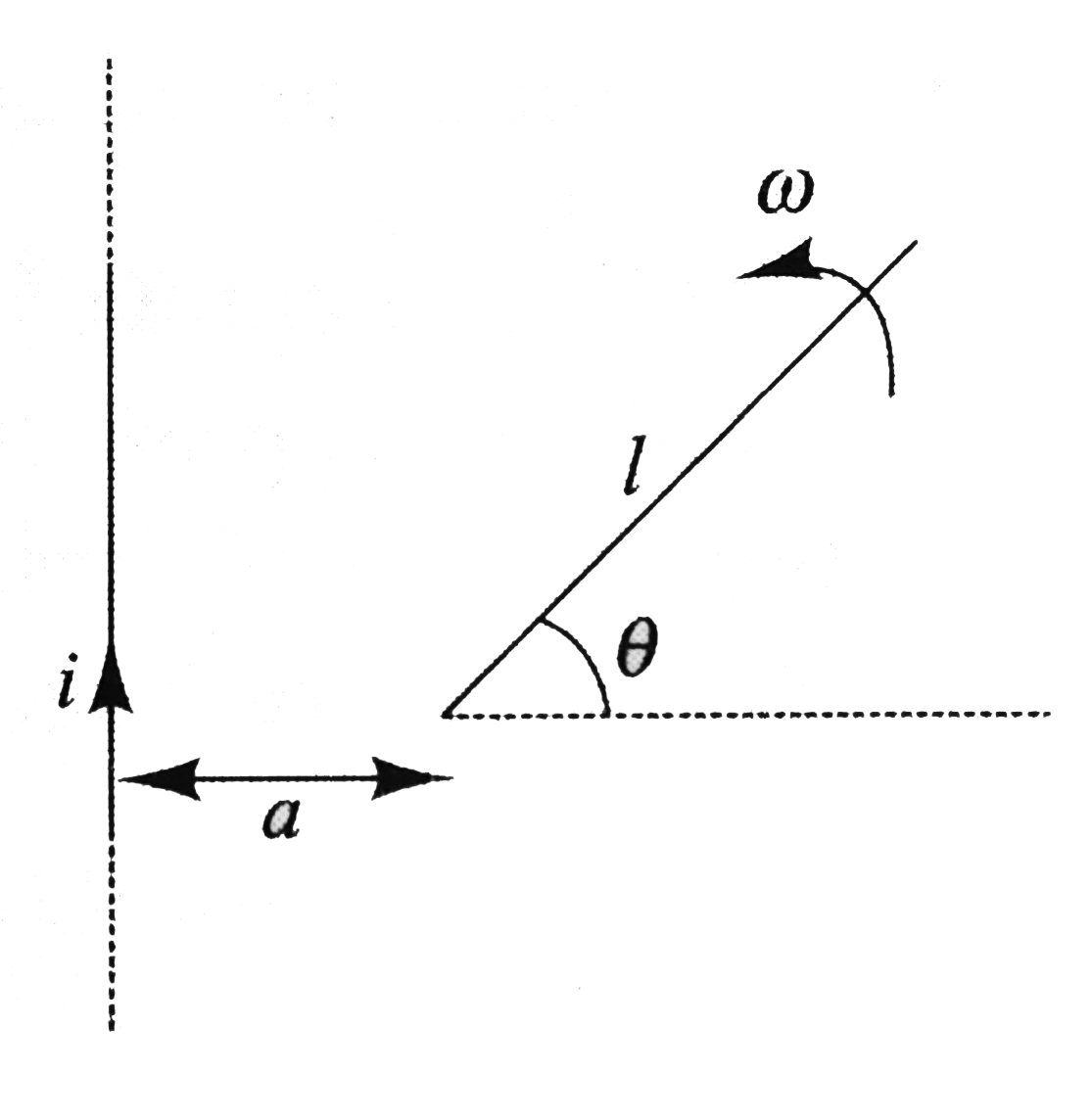
View SolutionA rod of length l is rotating with an angular speed ω about one of its ends which is at a distance a from an infinitely long wire carrying current i. Find the emf induced in the rod at the instant shown in .

View SolutionA wire of resistance 10Ω is bent to form a circle. P and Q are points on the circumference of the circle dividing it into a quadrant and are connected to a Battery of 3 V and internal resistance 1Ω as shown in the figure. The currents in the two parts of the circle are

View Solution
