A solid at temperature is kept in an evacuated chamber at temperature . The rate of increase of temperature of the body is propertional to
.
The correct Answer is:D
To solve the problem, we need to analyze the situation where a solid at a lower temperature T1 is placed in an evacuated chamber at a higher temperature T2. We want to find out what the rate of increase of temperature of the solid is proportional to.
1. Understanding the Setup:
- We have a solid with an initial temperature T1.
- This solid is placed in an evacuated chamber at a higher temperature T2 (where T2>T1).
- Since the chamber is evacuated, heat transfer occurs only through radiation.
Hint: Identify the temperatures involved and their relationship.
2. Applying the Stefan-Boltzmann Law:
- According to the Stefan-Boltzmann law, the power (rate of energy transfer) emitted by a body due to thermal radiation is given by:
P=σAT4
where P is the power, σ is the Stefan-Boltzmann constant, A is the surface area, and T is the absolute temperature in Kelvin.
Hint: Recall the formula for power in terms of temperature and understand that it applies to both the solid and the surrounding.
3. Rate of Heat Transfer:
- The solid will absorb radiation from the surrounding at temperature T2 and emit radiation at its own temperature T1.
- The rate of heat absorbed by the solid from the surroundings is proportional to T42.
- The rate of heat emitted by the solid is proportional to T41.
Hint: Write down the expressions for the power absorbed and emitted.
4. Net Rate of Heat Transfer:
- The net rate of heat transfer (which affects the rate of increase of temperature of the solid) can be expressed as:
Net Rate∝T42−T41
- This indicates that the increase in temperature of the solid is influenced by the difference in the fourth powers of the temperatures.
Hint: Think about how the difference in temperatures affects the net heat transfer.
5. Conclusion:
- Therefore, the rate of increase of temperature of the body is proportional to T42−T41.
- This matches with option 4 from the provided choices.
Hint: Compare your final expression with the options given in the question to confirm the answer.
Final Answer:
The rate of increase of temperature of the body is proportional to T42−T41.
- We have a solid with an initial temperature T1.
- This solid is placed in an evacuated chamber at a higher temperature T2 (where T2>T1).
- Since the chamber is evacuated, heat transfer occurs only through radiation.
- According to the Stefan-Boltzmann law, the power (rate of energy transfer) emitted by a body due to thermal radiation is given by:
P=σAT4
where P is the power, σ is the Stefan-Boltzmann constant, A is the surface area, and T is the absolute temperature in Kelvin.
- The solid will absorb radiation from the surrounding at temperature T2 and emit radiation at its own temperature T1.
- The rate of heat absorbed by the solid from the surroundings is proportional to T42.
- The rate of heat emitted by the solid is proportional to T41.
- The net rate of heat transfer (which affects the rate of increase of temperature of the solid) can be expressed as:
Net Rate∝T42−T41
- This indicates that the increase in temperature of the solid is influenced by the difference in the fourth powers of the temperatures.
- Therefore, the rate of increase of temperature of the body is proportional to T42−T41.
- This matches with option 4 from the provided choices.
The rate of increase of temperature of the body is proportional to T42−T41.
Topper's Solved these Questions
- HEAT TRANSFERBook:HC VERMA ENGLISHChapter:HEAT TRANSFERExercise:OBJECTIVE II
Explore 6 Videos
- HEAT TRANSFERBook:HC VERMA ENGLISHChapter:HEAT TRANSFERExercise:EXERCIESE
Explore 55 Videos
- HEAT TRANSFERBook:HC VERMA ENGLISHChapter:HEAT TRANSFERExercise:worked out examples
Explore 20 Videos
- HEAT AND TEMPERATUREBook:HC VERMA ENGLISHChapter:HEAT AND TEMPERATUREExercise:Objective 2
Explore 6 Videos
- INTRODUCTION TO PHYSICSBook:HC VERMA ENGLISHChapter:INTRODUCTION TO PHYSICSExercise:Question for short Answer
Explore 4 Videos
Similar Questions
A copper block of mass 'm' at temperature 'T1' is kept in the open atmosphere at temperature 'T2' where T2>T1. The variation of entropy of the copper block with time is best illustrated by
View SolutionOne end of a rod of length L and crosssectional area A is kept in a furnace at temperature T1. The other end of the rod is kept at a temperature T2. The thermal conductivity of the matrieal of the rod is K and emissivity of the rod is e. It is gives that T!=Ts+ΔT, where ΔT<<Ts,Ts is the temperature of the surroundings. If ΔT∝(T1−T2) find the proportional constant, consider that heat is lost only by rediation at the end where the temperature of the rod is T1.

View Solution
Knowledge Check
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
A solid copper sphere of density ρ, specific heat c and radius r is at temperature T1. It is suspended inside a chamber whose walls are at temperature 0K. What is the time required for the temperature of sphere to drop to T2? Take the emmissivity of the sphere to be equal to e.
View SolutionA solid sphere of radius 'R' density ρ and specific heat 'S' initially at temperature T0 Kelvin is suspended in a surrounding at temperature 0K. Then the time required to decrease the temperature of the sphere from T0 to T02 kelvin is (Assume sphere behaves like a black body)
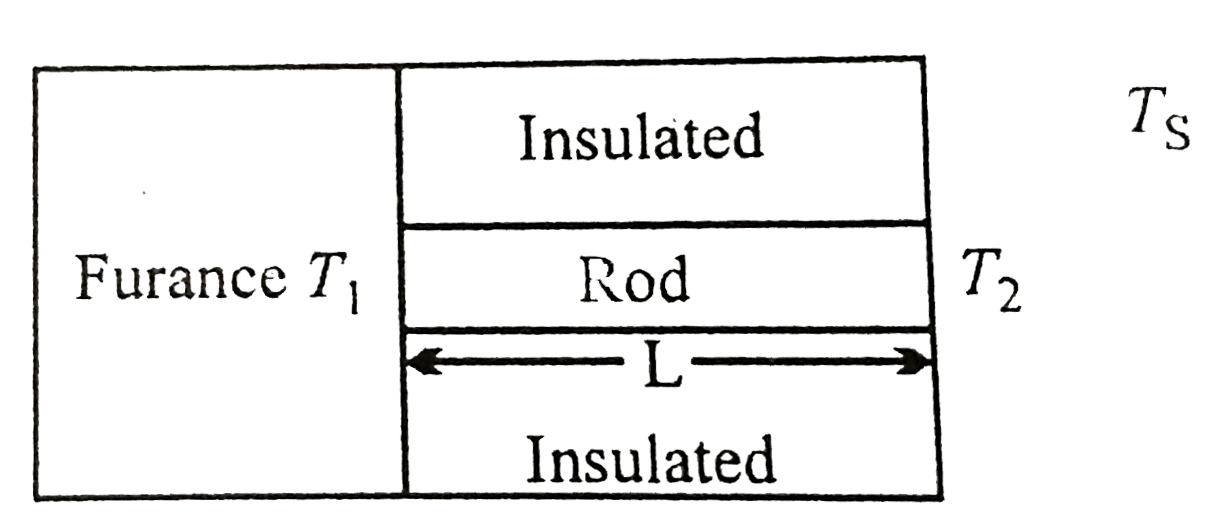
View SolutionOne end of rod of length L and cross-sectional area A is kept in a furance of temperature T1. The other end of the rod is kept at at temperature T2. The thermal conductivity of the material of the rod is K and emissivity of the rod is e. It is given that T2=TS+ΔT where ΔT<<TS, TS being the temperature of the surroundings. If ΔT∝(T1−TS), find the proportionality constant. Consider that heat is lost only by radiation at the end where the temperature of the rod is T2.
View SolutionThree Carnot engines operate in series between a heat source at a temperature T1 and a heat sink at temperature T4 (see figure). There are two other reservoirs at temperature T2andT3, as shown, with T1>T2>T3>T4. The three engines are equally efficient if :

View SolutionA black body of temperature T is inside a chamber of temperature T0 Now the closed chamber is slightly opened to Sun that temeperature of black body (T) and chamber (T0) remain constant .
View SolutionIn a dark room with ambient temperature T0, a black body is kept at a temperature T. Keeping the temperature of the black body constant (at T), sunrays are allowed to fall on the black body through a hole in the roof of the dark room. Assuming that there is no change in the ambient temperature of the room, which of the following statements (s) is/are correct ?
View SolutionSeven rods A, B, C, D, E, F and G are joined as shown in figure. All the rods have equal cross-sectional area A and length l. The thermal conductivities of the rods are KA=KC=K0, KB=KD=2K0, KE=3K0, KF=4K0 and KG=5K0 . The rod E is kept at a constant temperature T1 and the rod G is kept at a constant temperature T2(T2>T1) . (a) Show that the rod F has a uniform temperature T=(T1+2T2)/3 . (b) Find the rate of heat flowing from the source which maintains the temperature T2 .

View Solution
