A solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
11GMmR2
14GMmR2
GMm2R2
GMm4R2
The correct Answer is:C
To solve the problem of finding the gravitational force on a point mass m placed inside a spherical cavity of a solid sphere, we can follow these steps:
1. Understand the Setup:
- We have a solid sphere of mass M and radius R.
- There is a spherical cavity of radius R2 whose center is at a distance R2 from the center of the solid sphere.
- A point mass m is placed inside the cavity at a distance R4 from the center of the solid sphere.
2. Determine the Mass of the Cavity:
- The volume of the solid sphere is given by V=43πR3.
- The volume of the cavity is Vcavity=43π(R2)3=43πR38=16πR3.
- The mass of the cavity (which is the mass that is missing) can be calculated as:
Mcavity=M8
- This is because the density of the sphere remains constant, and the cavity occupies 18 of the volume of the sphere.
3. Calculate the Gravitational Field Inside the Sphere:
- The gravitational field g inside a solid sphere at a distance r from the center is given by:
g=GMinsider2
- Where Minside is the mass of the sphere that is at a distance r from the center.
- For our case, we need to consider the gravitational field due to the remaining mass of the sphere after removing the cavity.
4. Calculate the Gravitational Field at the Point Mass m:
- The distance of the point mass m from the center of the sphere is R4.
- The gravitational field due to the remaining mass of the sphere at this point is:
gremaining=G(M−Mcavity)(R4)2=G(M−M8)R216=G(7M8)R216=14GMR2
5. Consider the Effect of the Cavity:
- The gravitational field due to the cavity can be treated as a negative contribution since it is missing mass. The gravitational field due to the cavity at the point mass m is directed towards the center of the cavity.
- The distance from the center of the cavity to the point mass m is R4−R2=−R4.
- The gravitational field due to the cavity is:
gcavity=−GMcavity(R4)2=−G(M8)R216=−2GMR2
6. Combine the Gravitational Fields:
- The total gravitational field gtotal at the point mass m is:
gtotal=gremaining+gcavity=14GMR2−2GMR2=12GMR2
7. Calculate the Gravitational Force on Mass m:
- The gravitational force F on the mass m is given by:
F=m⋅gtotal=m⋅12GMR2
Final Answer:
The gravitational force on mass m is:
F=12GMmR2
- We have a solid sphere of mass M and radius R.
- There is a spherical cavity of radius R2 whose center is at a distance R2 from the center of the solid sphere.
- A point mass m is placed inside the cavity at a distance R4 from the center of the solid sphere.
- The volume of the solid sphere is given by V=43πR3.
- The volume of the cavity is Vcavity=43π(R2)3=43πR38=16πR3.
- The mass of the cavity (which is the mass that is missing) can be calculated as:
Mcavity=M8
- This is because the density of the sphere remains constant, and the cavity occupies 18 of the volume of the sphere.
- The gravitational field g inside a solid sphere at a distance r from the center is given by:
g=GMinsider2
- Where Minside is the mass of the sphere that is at a distance r from the center.
- For our case, we need to consider the gravitational field due to the remaining mass of the sphere after removing the cavity.
- The distance of the point mass m from the center of the sphere is R4.
- The gravitational field due to the remaining mass of the sphere at this point is:
gremaining=G(M−Mcavity)(R4)2=G(M−M8)R216=G(7M8)R216=14GMR2
- The gravitational field due to the cavity can be treated as a negative contribution since it is missing mass. The gravitational field due to the cavity at the point mass m is directed towards the center of the cavity.
- The distance from the center of the cavity to the point mass m is R4−R2=−R4.
- The gravitational field due to the cavity is:
gcavity=−GMcavity(R4)2=−G(M8)R216=−2GMR2
- The total gravitational field gtotal at the point mass m is:
gtotal=gremaining+gcavity=14GMR2−2GMR2=12GMR2
- The gravitational force F on the mass m is given by:
F=m⋅gtotal=m⋅12GMR2
The gravitational force on mass m is:
F=12GMmR2
Topper's Solved these Questions
Similar Questions
The figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

View Solution
Knowledge Check
A mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass m is
AGMm√2R2BGMm2R2CGMm2√2R2DGMm4R2
A cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionA cavity of radius R/2 is made inside a solid sphere of radius R. The centre of the cavity is located at a distance R/2 from the centre of the sphere. The gravitational force on a particle of a mass 'm' at a distance R/2 from the centre of the sphere on the line joining both the centres of sphere and cavity is (opposite to the centre of cavity). [Here g=GM/R2, where M is the mass of the solide sphere]
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View SolutionA solid spherical conductor of radius R has a spherical cavity of radius at its centre. A charge is kept at the centre. The charge at the inner surface, outer surface are respectively.
View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then
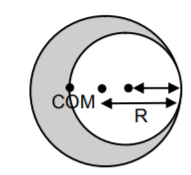
View SolutionA uniform solid sphere of radius R has a cavity of radius 1m cut from it if centre of mass of the system lies at the periphery of the cavity then

View Solution
