A solid sphere of mass m=2kg and density ρ=500kg/m3 is held stationary relative to a tank filled with water. The tank is acceerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank. (Density of water=1000kg/m3,g=10m/s2)

Density of the spherical material = specific gravity × density of water =sr
its volme is V=msρ
Hence mass of water displaced by the shere is
Vρ=msρρ=m/s=20.5=4kg
since, the tank is accelerating upwards with acceleration a therefore, apparent value of gravitational acceleration is
g'=g+a=12ms−2
Hence, upthrust exerted by water on the sphere is
F=Vρ(g+a)=48N brgt 
F=mg−T=ma=.T=F−mg−ma=24N
When thread snaps, tension T disappears. Let the sphere now starts accelerating upwards with acceleration b. Considering the free body diagram.
F−mg=mb
∴b=14ms−2
Thus is the absolute acceleration of the sphere. But the tank itself is accelerating upwards with acceleration a. Therefore, upward acceleration of the sphere relative to the tank is b−a=12ms−2
Topper's Solved these Questions
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Solved Examples
7 Videos
- FLUID MECHANICSBOOK - CENGAGE PHYSICSCHAPTER - FLUID MECHANICSEXERCISE - Exercise 4.1
11 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICSCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - INTEGER_TYPE
1 Video
Similar Questions
A solid sphere of mass m=2kg and specific gravity s=0.5 is held stationary relative to a tank filled with water. The tank is accelerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank.
(Density of water =1000kgm−3,g=10ms−2).
 .
.
View SolutionA block of mass 1 kg and density 0.8g/cm3 is held stationary with the help of a string as shown in figure. The tank is accelerating vertically upwards with an acceleration a =1.0m/s2. Find

(a) the tension in the string,
(b) if the string is now cut find the acceleration of block.
(Take g=10m/s2 and density of water =103kg/m3).
View Solution
Knowledge Check
The mass of lift is 500 kg. When it ascends with an acceleration of 2m/s2,the tension in the cable will be [g=10m/s2]
A6000 NB5000 NC4000 ND50 NA wooden block of mass 1kg and density 800Kgm−3 is held stationery, with the help of a string, in a container filled with water of density 1000kgm−3 as shown in the figure. If the container is moved upwards with an acceleration of 2ms−2, then the tension in the string will be ( takeg=10ms−2)
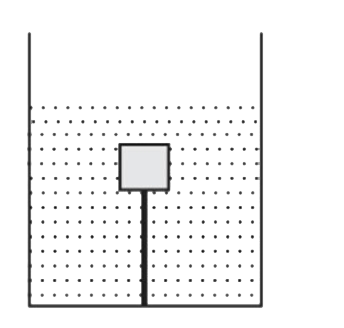 A2NB3NC5ND6N
A2NB3NC5ND6N
Calculate the water pressure and the thrust at the bottom of a tank whose length width and the depth are 2m, 1.5 m and 1m respectively. Density of water is 1000kgm−3
View SolutionCalculate the total pressure at the bottom of a lake of depth 5.1 m (atm pressure =105 P), density of water =103kg/m3,g=10m/s2
View SolutionCalculate the water pressure and the thrust at the bottom of a tank whose length width and the depth are 2m, 1.5 m and 1m respectively. Density of water is 1000kgm−3
View SolutionA raectangular tank 2 m deep, 5 m broad and 10 m long is filied with water . Calculate the thrust on each of the sides and on the base . Density of water 1000kgm−2andg=9.8ms−2)
View SolutionCalculate the molarity of water if its density is 1000kg/m3.
View SolutionCalculate the molarity of water if its density is 1000kg/m3.
View Solution
