A solid sphere of radius R and density ρ is attached to one end of a mass-less spring of force constant k. The other end of the spring is connected to another solid sphere of radius R and density 3ρ. The complete arrangement is placed in a liquid of density 2ρ and is allowed to reach equilibrium. The correct statements(s) is (are)
(a) The net elongation of the spring is 4πR3ρg3k
(b) The net elongation of the spring is 8πRρg3k
(c) The light sphere is partially submerged
(d) The light sphere is completely submerged
The correct Answer is:A, D
Consider the equilibrium of the system of both spheres and the spring

The weight of system
=43πR3(3ρ)g+43πR3ρg=4[43πR3ρg]
This is to be balanced by the buoyant force. This can be possible only when the light sphere is completely submerged. In this way the buoyant force

B=[(43πR3)×2]×(2ρ)×g=4[43πR3ρg]
Now considering the equilibrium of the heavy sphere Fs+B=W
∴Fs=W−B
∴Kx=43πR3(3ρ)g−43πR3(2ρ)g
:x=43πR3ρgK
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Video
- LAWS OF MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - LAWS OF MOTIONEXERCISE - JEE Main And Advanced
79 Videos
- MOMENTUM & IMPULSEBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOMENTUM & IMPULSEEXERCISE - JEE Main And Advanced
30 Videos
Similar Questions
A sphere of radius R contains charge density ρ(r)=A(R−r), for 0<r<R. The total electric charge inside the sphere is Q.
The electric field inside the sphere is
View SolutionA hollow sphere of external radius R and thickness t (< < R) is made of a metal of density ρ. The sphere will float in water if
View Solution
Knowledge Check
A sphere of radius R and density ρ1 is dropped in a liquid of density σ. Its terminal velocity is v1. If another sphere of radius R and density ρ2 is dropped in the same liquid, its terminal velocity will be:
A(ρ2−σρ1−σ)v1B(ρ1−σρ1−σ)v1C(ρ1ρ2)v1D(ρ2ρ1)v1
A solid hemisphere of radius R is made to just sink in a liquid of density ρ find theAπR3ρg3BπR3ρg2C0DπR3ρgWhat is the moment of inertia of a solid sphere of density ρ and radius R about its diameter ?
A105176R5ρB176105R5ρC105176R2ρD176105R2ρ
A solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
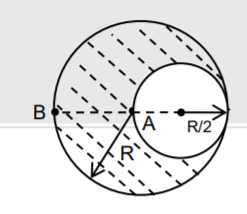
View SolutionIf ρ is density of the material of a sphere of radius R . Then its moment of inertia about its diameter is
View SolutionIn the figure shown, the heavy cylinder (radius R) reasting on a smooth surface separates two liquids of densities 2ρ and 3ρ. The height h for the equilibrium of cylinder must be
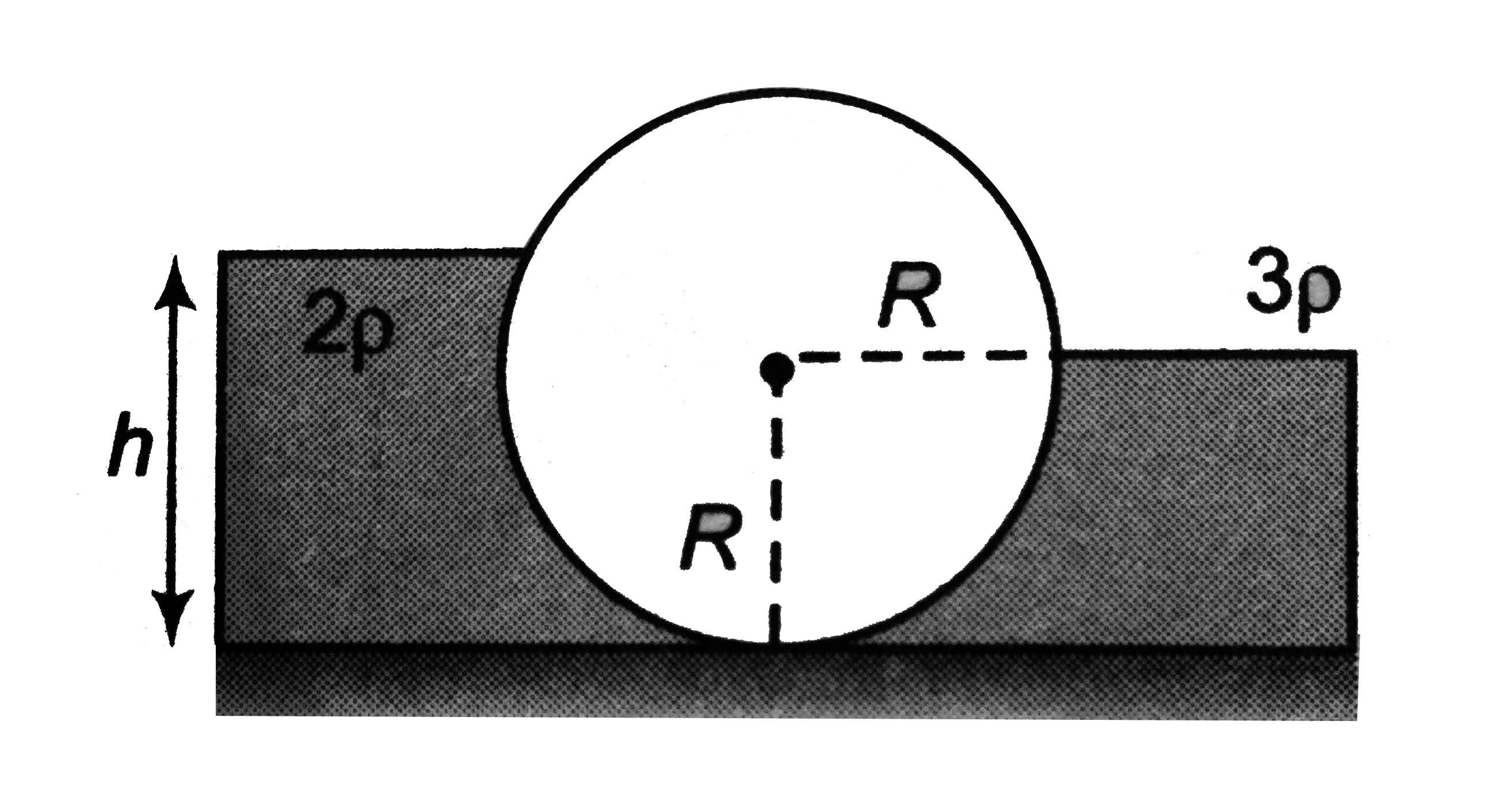
View SolutionA Solid sphere of density ρ=ρ0(1−r2R2),0<r≤R just floats in a liquid then density of liquid is– (r is distance from centre of sphere)
View SolutionWhat is the moment of inertia of solid sphere of density ρ and radius R about its diameter ?
View Solution