A solid sphere of radius R is floating in a liquid of density ρ with half of its volume submerged. If the sphere is slightly pushed and released, it starts performing simple harmonic motion. Find the frequency of these oscillations.
The correct Answer is:12π√3g2R
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - ASSERTION-REASON TYPE
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - PROBLEM SET - II
32 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - CBSE SCANNER
10 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - CBSE SCANNER
3 Videos
Similar Questions
A solid sphere of radius R is floating in a liquid of density σ with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
View SolutionA solid sphere of radius R is floating in a liquid of density σ with half of its volume submerged. If the sphere is slightly pushed and released , it starts axecuting simple harmonic motion. Find the frequency of these oscillations.
View Solution
Knowledge Check
If the period of oscillation of particle performing simple harmonic motion is 8 s, than the frequency of its kinetic energy will be
A0.5s−1B0.25s−1C1s−1D2s−1A wooden cube (density of wood 'd') of side 'l' flotes in a liquid of density 'ρ' with its upper and lower surfaces horizonta. If the cube is pushed slightly down and released, it performs simple harmonic motion of period 'T'. Then, 'T' is equal to :-
A2π√lρ(ρ−d)gB2π√ldρgC2π√lρdgD2π√ld(ρ−d)gA pendulum of mass m and length L is connected to a spring as shown in figure. If the bob is displaced slightly from its mean position and released, it performs simple harmonic motion. The angular frequency of the oscillation of bob is
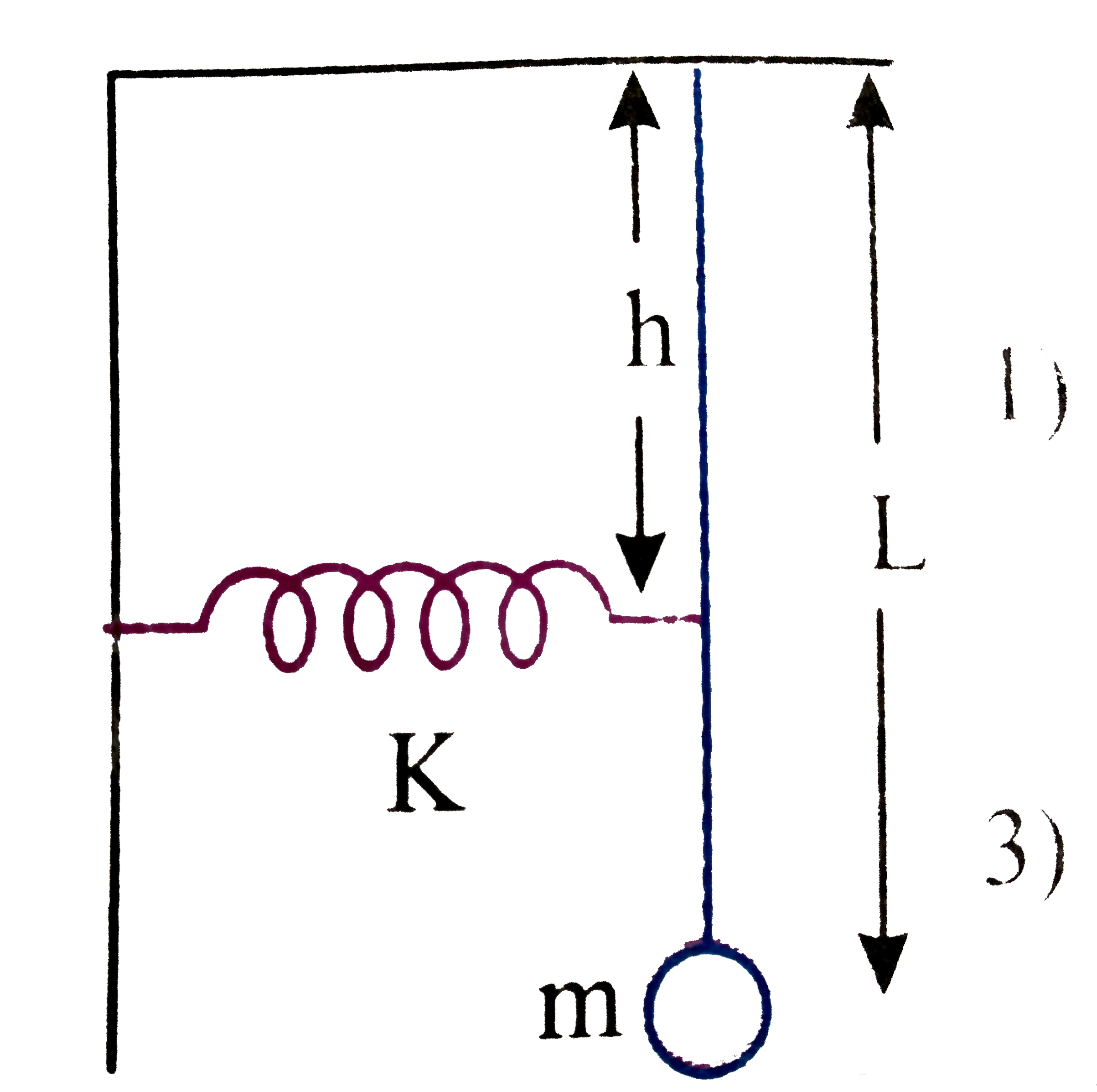 A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A√gLB√Kh2+mgLmL2C√3gLD√Kh2mL2
A wooden cube (density of wood ρ3 ') of side l 'floats in a liquid of density ' ρ with its upper and lower surfaces horizontal. If the cube is pushed slightly down and released, it performs simple harmonic motion of period T. Then, T is equal to 2π√xlyg. Find (x+y).
View SolutionA wooden cube (density of wood 'd') of side 'l' flotes in a liquid of density 'ρ' with its upper and lower surfaces horizonta. If the cube is pushed slightly down and released, it performs simple harmonic motion of period 'T'. Then, 'T' is equal to :-
View SolutionA solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View SolutionA solid sphere of density σ with one -third of tis volume submerged . When the sphere is pressed down slightly and released , it executes S.H.M of time period T. Then (viscous effect is ignored)
View SolutionA solid cube of side a and density ρ0 floats on the surface of a liquid of density ρ. If the cube is slightly pushed downward, then it oscillates simple harmonically with a period of
View Solution
