A small sphere is placed inside a concave glass vessel kept on a horizontal table. The radius of curvature of the concave vessel is 1.09 m. If the small sphere is displaced slightly from its position of equilibrium and then released, what will be the time period of the simple harmonic motion that the sphere would execute? g=9.81m⋅s−2
The correct Answer is:2.09 s
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - ASSERTION-REASON TYPE
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
- SIMPLE HARMONIC MOTIONBOOK - CHHAYA PUBLICATIONCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - PROBLEM SET - II
32 Videos
- ROTATION OF RIGID BODIES BOOK - CHHAYA PUBLICATIONCHAPTER - ROTATION OF RIGID BODIES EXERCISE - CBSE SCANNER
10 Videos
- STATICSBOOK - CHHAYA PUBLICATIONCHAPTER - STATICSEXERCISE - CBSE SCANNER
3 Videos
Similar Questions
A small lead sphere is made to execute shm inside a concave dish of radius of curvature 1 m. What is its period ?
View SolutionA block A of mass m1 is placed on a horizontal frictionless table. It is connected to one end of a light spring of force constant k whose other end is fixed to a wall. A small block B of mass m2 is placed on block A. The coefficient of static friction between the blocks is μ. The system is displaced slightly from its equilibrium position and released. What is the maximum amplitude of the resulting simple harmonic motion of the system so that the upper block does not slip over the lower block ?
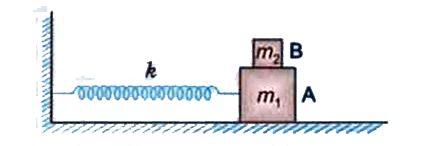
View Solution
Knowledge Check
A sphere of catius r is kept on a concave of mirror radius of curation R. The arrangement a kept on a horizontal tavke (the surface of concave mirror is fricationless and sliding not rolling). If the sphere is displaced from its equilibrium position and left, then it executes S.h.M. The period of oscillation will be
A2π ⎷((R−r)1.44)B2π√(R−rg)C2π√(rRa)D2π√(Rgr)
A sphere of radius r is kept on a concave mirror of radius of curation R. The arrangement is kept on a horizontal surface (the surface of concave mirror is friction less and sliding not rolling). If the sphere is displaced from its equilibrium position and left, then it executes S.h.M. The period of oscillation will be
View SolutionA small sphere is placed on a concave mirror of radius of curvature 'R' a little away from the centre.When the sphere is released it oscillates.Assuming the oscillation to be simple harmonic its time period is
View SolutionA small compass needle of magnetic moment 'm' and moment of inertia 'l' is free to oscillate in a magnetic field 'B'. It is slightly disturbed from its equilibrium position and then released. Show that it executes simple harmonic motion. Hence, write the expression for its time period.
View SolutionA small compass needle of magnetic moment ‘M’ and moment of inertial ‘I’ is free to oscillate in a magnetic field ‘B’. It is slightly disturbed from its equilibrium position and then released. Show that it executes simple harmonic motion. Hence, write the expression for its time period.
View SolutionA small compass needle of magnetic moment ‘M’ and moment of inertial ‘I’ is free to oscillate in a magnetic field ‘B’. It is slightly disturbed from its equilibrium position and then released. Show that it executes simple harmonic motion. Hence, write the expression for its time period.
View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
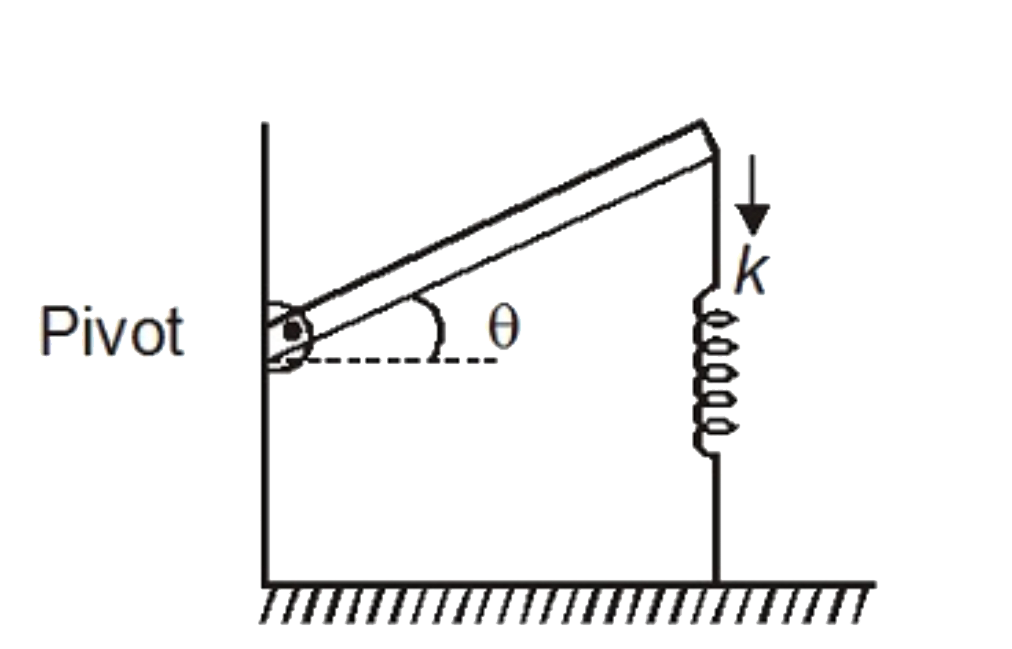
View SolutionA horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is

View Solution
