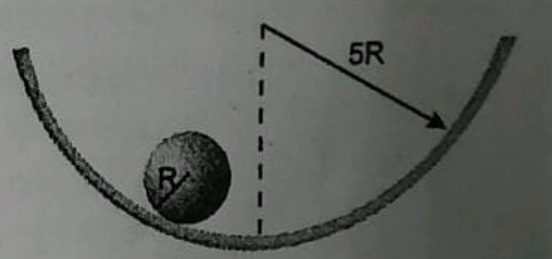
A solid sphere $(r a d i u s = R)$ rolls without slipping in a cylindrical throuh $(r a d i u s = 5 R)$ . Findthe time period of small oscillations.

Video Solution

Text Solution

Verified by Experts

Let us locate solide cylinder when it is displaced from its stable equilibrium position by the small angle $θ$ during its oscialltion ( figure). If $v_{c}$ be the instantaneous speed of the $C . M . (C)$ of the solid cylinder which is in pure rolling, then its angular velocity about its own centre $C$ is
$ω = \frac{v_{c}}{r} ... (1)$
Since $C$ moves in a circle of radius $(R - r)$ , the speed of $C$ at the same moment can be written as
$v_{c} = . θ (R - r) . . (2)$
Thus from Eqns $(1)$ and $(2)$
$ω = . θ \frac{(R - r)}{r} ... (3)$
As a mechanical energy of oscillation of the solide cylinder is conserved, $i . e . E = T + U =$ constant
So, $\frac{1}{2} m v_{c}^{2} = \frac{1}{2} I_{c} ω^{2} + m g (R - r) (1 - cos θ) =$ constant
(Where $m$ is the mass of solid cylinder and $I_{c}$ is the moment of inertia of the solide cylinder about an axis passing through its $C . M . (C)$ and perpendicular to the plane of figure, of solide cylinder $)$
or, $\frac{1}{2} m ω^{2} r^{2} + \frac{1}{2} \frac{m r^{2}}{2} ω^{2} + m g (R_{r}) (1 - cos θ) =$ constant $($ using Eqn and $I_{c} = m r /)$
$\frac{3}{4} r^{2} (. θ) \frac{{(R - r)}^{2}}{r^{2}} + g (R - r) (1 - cos θ) =$ constant, $($ using Eqn. 3 $)$
Differentiating w.r.t. time
$\frac{3}{4} (R - r) 2 . θ .. θ + g sin θ . θ = 0$
So, $.. θ = - \frac{2 g}{3 (R - r)} θ$ ,( because for small $θ, sin θ ≅ θ)$
Thus $ω_{0} = \sqrt{\frac{2 g}{3 (R - r)}}$
Hence the sought time period
$T = \frac{2 π}{ω_{0}} = 2 π \sqrt{\frac{3 (R - r)}{2 g}}$

Updated on:21/07/2023

A small solid sphere of radius $r$ rolls down an incline without slipping which ends into a vertical loop of radius $R$ . Find the height above the base so that it just loops the loop
A $\frac{5}{2} R$
B $\frac{5}{2} (R - r)$
C $\frac{25}{10} (R - r)$
D $\frac{27}{10} R - \frac{17 r}{10}$
A solid sphere of mass $m$ and radius $R$ rolls without slipping on a horizontal surface such that $v_{c . m .} = v_{0}$ .
AThe kinetic energy of rotation is $\frac{1}{5} m v_{0}^{2}$ .
BThe total kinetic energy is $\frac{7}{10} m v_{0}^{2}$ .
CThe mechanical energy (assume the ground as reference) is $m g R + \frac{7}{10} m v_{0}^{2}$ .
DAll options are correct.
A solid sphere of mass m rolls without slipping on an inclined plane of inclination $θ$ . The linear acceleration of the sphere is
A $\frac{7}{5} g sin θ$
B $\frac{2}{7} g sin θ$
C $\frac{3}{7} g sin θ$
D $\frac{5}{7} g sin θ$