A solid uniform sphere rotating about its axis with kinetic energy E1 is gently placed on a rough horizontal plane at time t=0, Assume that, at time t=t1, it starts pure rolling and at that instant total KE of the sphere is E2. After sometime, at time t=t2. KE of the sphere is E3. Then
E1=E2=E3
E1>E2=E3
E1>E2>E3
E1<E2=E3
The correct Answer is:B
To solve the problem step by step, we will analyze the kinetic energy of the solid uniform sphere at different times as it transitions from pure rotation to pure rolling.
Step 1: Initial Kinetic Energy (E1)
At time t=0, the solid uniform sphere is rotating about its axis. The total kinetic energy E1 consists of two components:
- Rotational kinetic energy due to its rotation about its axis.
- Translational kinetic energy is zero since it is not moving linearly.
The formula for the rotational kinetic energy Erot of a solid sphere is given by:
Erot=12Iω2
where I is the moment of inertia and ω is the angular velocity. For a solid sphere, I=25mr2.
Thus, we can express E1 as:
E1=12Iω2=12(25mr2)ω2=15mr2ω2
Step 2: Transition to Pure Rolling (E2)
At time t=t1, the sphere is placed on a rough horizontal plane. Due to friction, the sphere will start to roll without slipping. As it transitions to pure rolling, some of the rotational kinetic energy is converted into translational kinetic energy due to the work done against friction.
At this point, the total kinetic energy E2 will be less than E1 because energy is lost to friction:
E2<E1
Step 3: Pure Rolling Condition
When the sphere starts pure rolling, the condition for pure rolling is:
v=rω
where v is the linear velocity of the center of mass. At this moment, the kinetic energy E2 can be expressed as:
E2=12mv2+12Iω2
Substituting v=rω into the equation gives:
E2=12m(rω)2+12(25mr2)ω2
This simplifies to:
E2=12mr2ω2(1+25)=710mr2ω2
Step 4: Kinetic Energy After Some Time (E3)
At time t=t2, the sphere continues to roll without slipping. Since there is no friction acting on it anymore (as it is already rolling), the total kinetic energy E3 will remain constant:
E3=E2
Conclusion
From the analysis, we can conclude:
- E1>E2 (because energy is lost due to friction)
- E2=E3 (because there is no further energy loss once pure rolling starts)
Thus, the correct relationship is:
E1>E2=E3
Final Answer
The correct option is:
E1>E2=E3
At time t=0, the solid uniform sphere is rotating about its axis. The total kinetic energy E1 consists of two components:
- Rotational kinetic energy due to its rotation about its axis.
- Translational kinetic energy is zero since it is not moving linearly.
Erot=12Iω2
where I is the moment of inertia and ω is the angular velocity. For a solid sphere, I=25mr2.
E1=12Iω2=12(25mr2)ω2=15mr2ω2
At time t=t1, the sphere is placed on a rough horizontal plane. Due to friction, the sphere will start to roll without slipping. As it transitions to pure rolling, some of the rotational kinetic energy is converted into translational kinetic energy due to the work done against friction.
E2<E1
When the sphere starts pure rolling, the condition for pure rolling is:
v=rω
where v is the linear velocity of the center of mass. At this moment, the kinetic energy E2 can be expressed as:
E2=12mv2+12Iω2
Substituting v=rω into the equation gives:
E2=12m(rω)2+12(25mr2)ω2
This simplifies to:
E2=12mr2ω2(1+25)=710mr2ω2
At time t=t2, the sphere continues to roll without slipping. Since there is no friction acting on it anymore (as it is already rolling), the total kinetic energy E3 will remain constant:
E3=E2
From the analysis, we can conclude:
- E1>E2 (because energy is lost due to friction)
- E2=E3 (because there is no further energy loss once pure rolling starts)
E1>E2=E3
The correct option is:
E1>E2=E3
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - A Only One Option is Correct86videos
ROTATIONAL MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - More than one option is correct36videos
ROTATIONAL MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions2videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct3videos
SEMICONDUCTORS AND ELECTRONIC DEVICES
Similar Questions
A solid sphere of radius 2.45m is rotating with an angular speed of 10rad/s. When this rotating sphere is placed on a rough horizontal surface then after sometime it starts pure rolling. Find the linear speed of the sphere after it starts pure rolling.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
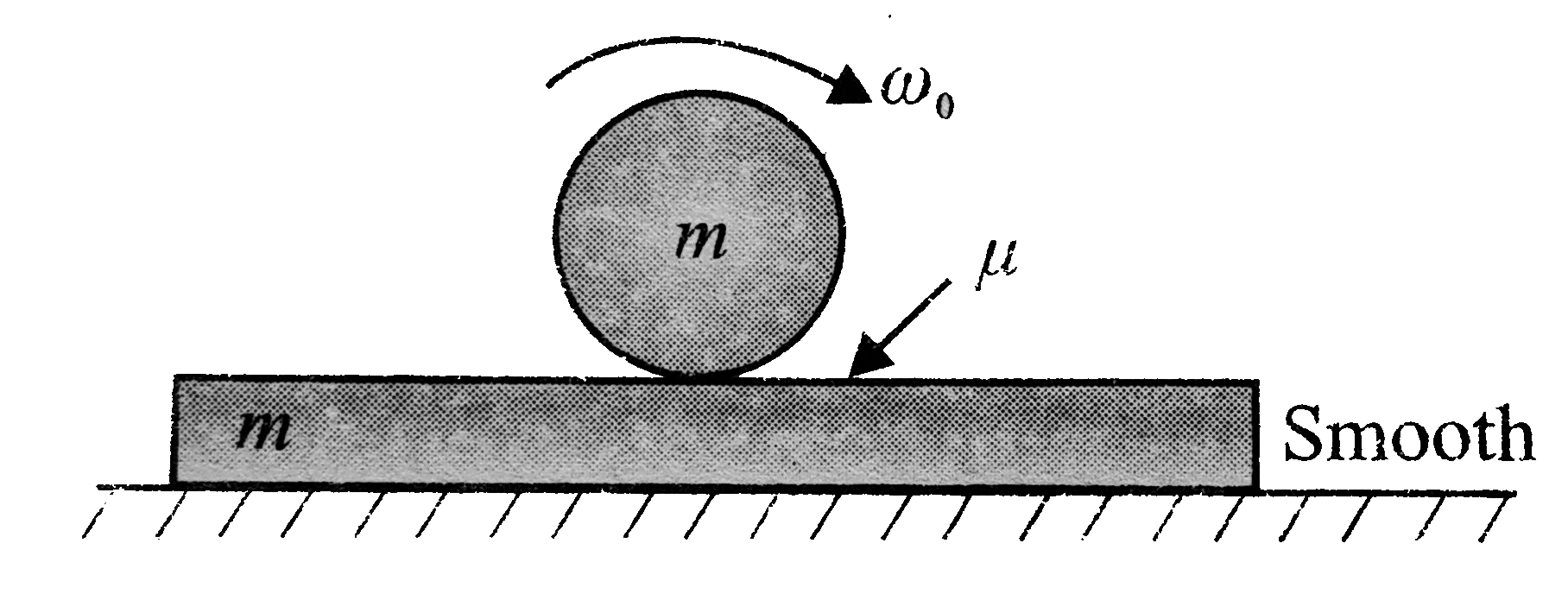
Find the time t at which the pure roiling startsView Solution
Knowledge Check
- Question 1 - Select One
A ring of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a rough horizontal table. The coefficient of kinetic friction is μk. The time after it starts rolling is.
AωoμkR2gBωog2μkRC2ωoRμkgDωoR2μkg
A solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity ω0. Once the pure rolling starts let v1 and v2 be the linear speeds of their centres of mass. Then
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.View SolutionThe coordinates of a particle moving in XY-plane at any instant of time t are x=4t2,y=3t2. The speed of the particle at that instant is
View SolutionA solid sphere is in rolling motion. In rolling motion a body prosseses translational kinetic energy (Kt) as well as rotational kinetic energy (Kr) simutaneously. The ratio
Kt:(Kt+Kr) for the sphere isView SolutionA non conducting solid sphere of mass m and radius R having uniform charge density +ρ and −ρ as shown in figure. It is then placed on a rough non conducting horizontal plane. At t=0 a uniform electric field →E=E0ˆiN/C is switched on and the solid sphere starts rolling with sliding. The magnitude of frictional force at t=0 is 2ρπR3E0K. Find the value of K
 View Solution
View SolutionKinetic energy of a charged particle is zero at time t0. K at time 2 t0. 2K at time 3 t0. It remains constant (i.e.2K) upto 4 t0. Choose the correct option.
View SolutionA sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
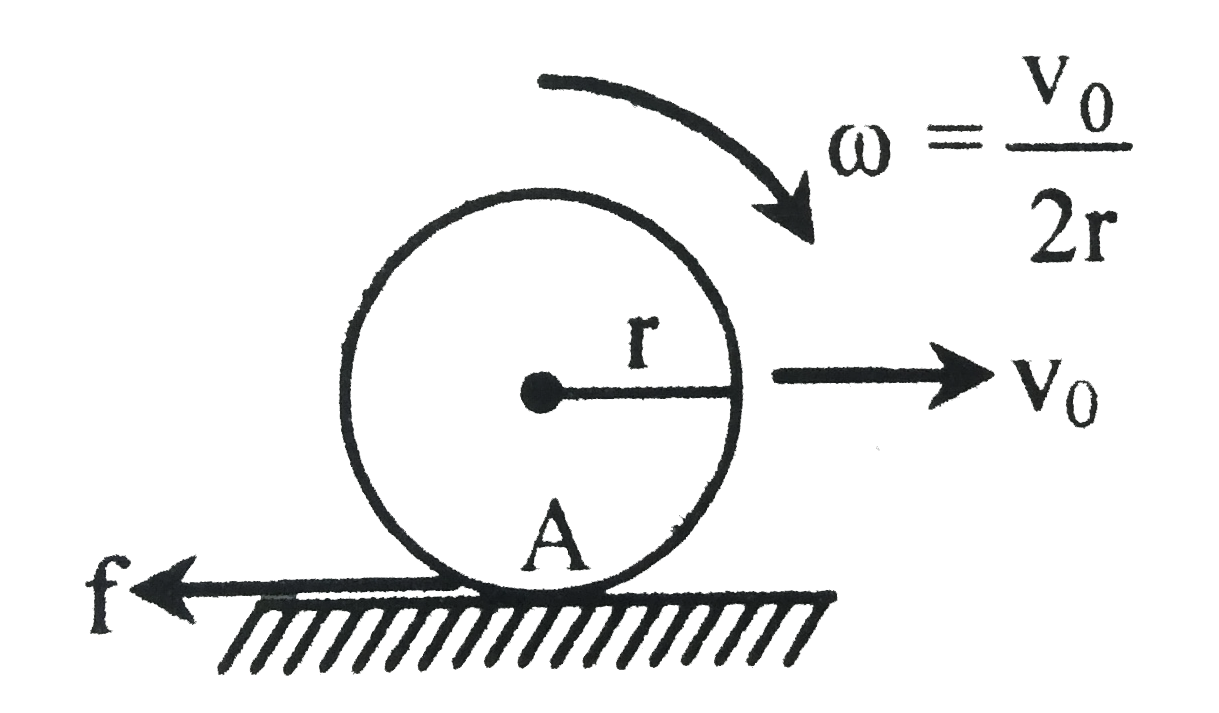 .View Solution
.View Solution

