A sonometer wire supports a 4 kg load and vibrates in fundamental mode with a tunig fork of frequency 416 Hz. The length of the wire between the bridges is now doubled. In order to maintain fundamental mode, the load should be changed to
1 kg
2 kg
8 kg
16 kg
The correct Answer is:D
To solve the problem step by step, we will use the relationship between the fundamental frequency of a vibrating string, its length, tension, and mass per unit length.
Step 1: Understand the fundamental frequency formula
The fundamental frequency f of a vibrating string is given by the formula:
f=12L√Tμ
where:
- L = length of the string
- T = tension in the string
- μ = mass per unit length of the string
Step 2: Calculate the initial conditions
In the initial case, we have:
- Load m1=4kg
- Tension T1=m1⋅g=4⋅10=40N (taking g≈10m/s2)
- Length L1
Using the fundamental frequency:
f=12L1√40μ
Step 3: Set up the equation for the new conditions
When the length of the wire is doubled, the new length L2=2L1. We want to maintain the same fundamental frequency f.
For the new conditions, let the new mass be m2 and the new tension be:
T2=m2⋅g
The equation for the new fundamental frequency becomes:
f=12L2√T2μ=14L1√m2⋅gμ
Step 4: Equate the two frequencies
Since we want the frequencies to remain the same:
12L1√40μ=14L1√m2⋅gμ
Step 5: Simplify the equation
Cancel L1 and μ from both sides:
12√40=14√m2⋅g
Step 6: Cross-multiply and square both sides
Cross-multiplying gives:
2√40=√m2⋅g
Squaring both sides results in:
4⋅40=m2⋅g
160=m2⋅g
Step 7: Solve for m2
Now, substituting g≈10m/s2:
m2=16010=16kg
Conclusion
To maintain the fundamental mode after doubling the length of the wire, the load should be changed to 16 kg.
---
The fundamental frequency f of a vibrating string is given by the formula:
f=12L√Tμ
where:
- L = length of the string
- T = tension in the string
- μ = mass per unit length of the string
In the initial case, we have:
- Load m1=4kg
- Tension T1=m1⋅g=4⋅10=40N (taking g≈10m/s2)
- Length L1
f=12L1√40μ
When the length of the wire is doubled, the new length L2=2L1. We want to maintain the same fundamental frequency f.
T2=m2⋅g
f=12L2√T2μ=14L1√m2⋅gμ
Since we want the frequencies to remain the same:
12L1√40μ=14L1√m2⋅gμ
Cancel L1 and μ from both sides:
12√40=14√m2⋅g
Cross-multiplying gives:
2√40=√m2⋅g
4⋅40=m2⋅g
160=m2⋅g
Now, substituting g≈10m/s2:
m2=16010=16kg
To maintain the fundamental mode after doubling the length of the wire, the load should be changed to 16 kg.
Topper's Solved these Questions
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Objective -2
9 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Exercises
57 Videos
- WAVE MOTION AND WAVES ON A STRINGBOOK - HC VERMA ENGLISHCHAPTER - WAVE MOTION AND WAVES ON A STRINGEXERCISE - Worked out Examples
10 Videos
- THE FORCESBOOK - HC VERMA ENGLISHCHAPTER - THE FORCESEXERCISE - Questions for short Answer
9 Videos
- WORK AND ENERGYBOOK - HC VERMA ENGLISHCHAPTER - WORK AND ENERGYEXERCISE - Question for Short Answer
16 Videos
Similar Questions
A sonometer wire of length l vibrates in fundamental mode when excited by a tunning fork of frequency 416 Hz. If the length is double keeping other things same the string will
View SolutionA stone in hung in air from a wire which is stretched over a sonometer . The bridges of the sonometer are 40cm apart when the wire is in unison with a tuning fork of frequency 256Hz. When the stone is completely immersed in water , the length between the bridges is 22cm for re - establishing unison . The specific gravity of the material of the stone is
View Solution
Knowledge Check
A tuning fork of frequency 440 Hz resonates with a tube closed at one end of length 18 cm and diameter 5 cm in fundamental mode. The velocity of sound in air is
A1. 336ms−1B2. 343ms−1C3. 300ms−1D4. 350ms−1
A sonometer wire having a length of 1.50 m between the bridges vibrates in its second harmonic in resonance with a tuning fork of frequency 256 Hz. What is the speed of the transverse wave on the wire ?
View SolutionA stone is hung in air from a wire which is stretched over a sonometer. The bridges of the sonometer are L cm apart when the wire is in unison with a tuning fork of frequency N . When the stone is completely immersed in water, the length between the bridges is l cm for re-establishing unison, the specific gravity of the material of the stone is
View SolutionA sonometer wire under a tension of 10kg weight is in unsion with a tuning fork of frequency 320HZ . To make the wire vibrate in unsion with a tuning fork of frequency 256hZ , the tension should be altered by
View SolutionA sonometer wire , 100cm in length has fundamental frequency of 330Hz. The velocity of propagation of tranverse waves along the wire is
View SolutionFundamental frequency of a sonometer wire is n. If
the length and diameter of the wire are doubled
keeping the tension same, then the new fundamental
frequency is
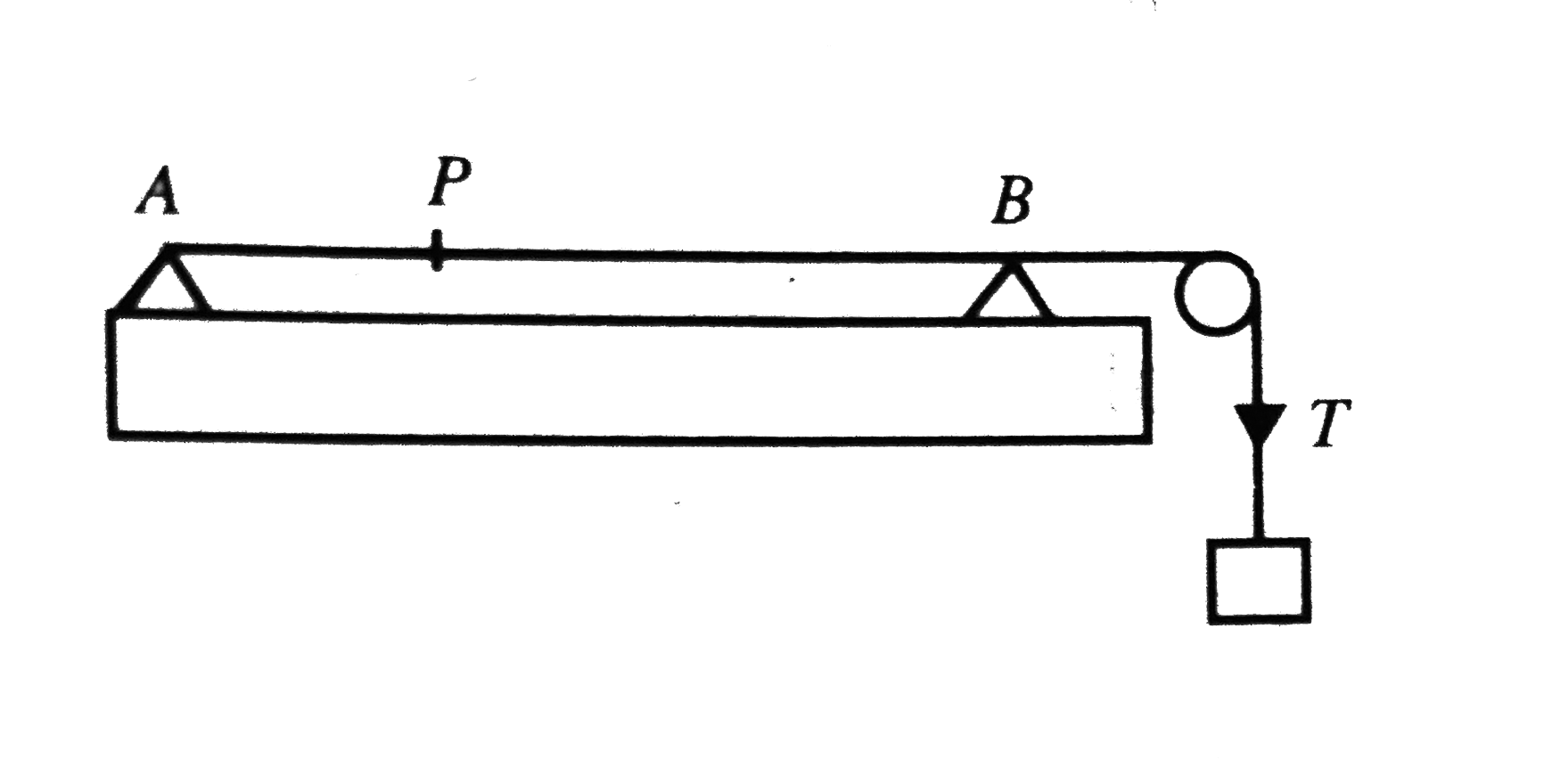
View SolutionA sonometer strings AB of length 1m is stretched by a load and the tension T is adjusted so that the string resonates to a frequency of 1kHz. Any point P of the wire may be held fixed by use of a movable bridge that can slide along the base of sonometer.
View SolutionA sonometer wire under tension of 63 N vibrating in its fundamental mode is in resonance with a vibrating tuning fork. The vibrating portion of that sonometer wire has a length of 10 cm and a mass of 1 g. The vibrating tuning fork is now moved away from the vibrating wire with a constant speed and an observer standing near the sonometer hears one beat per second. Calculate the speed with which the tuning fork is moved if the speed of sound in air is 300 m/s.
View Solution
