A sonometer strings AB of length 1m is stretched by a load and the tension T is adjusted so that the string resonates to a frequency of 1kHz. Any point P of the wire may be held fixed by use of a movable bridge that can slide along the base of sonometer.
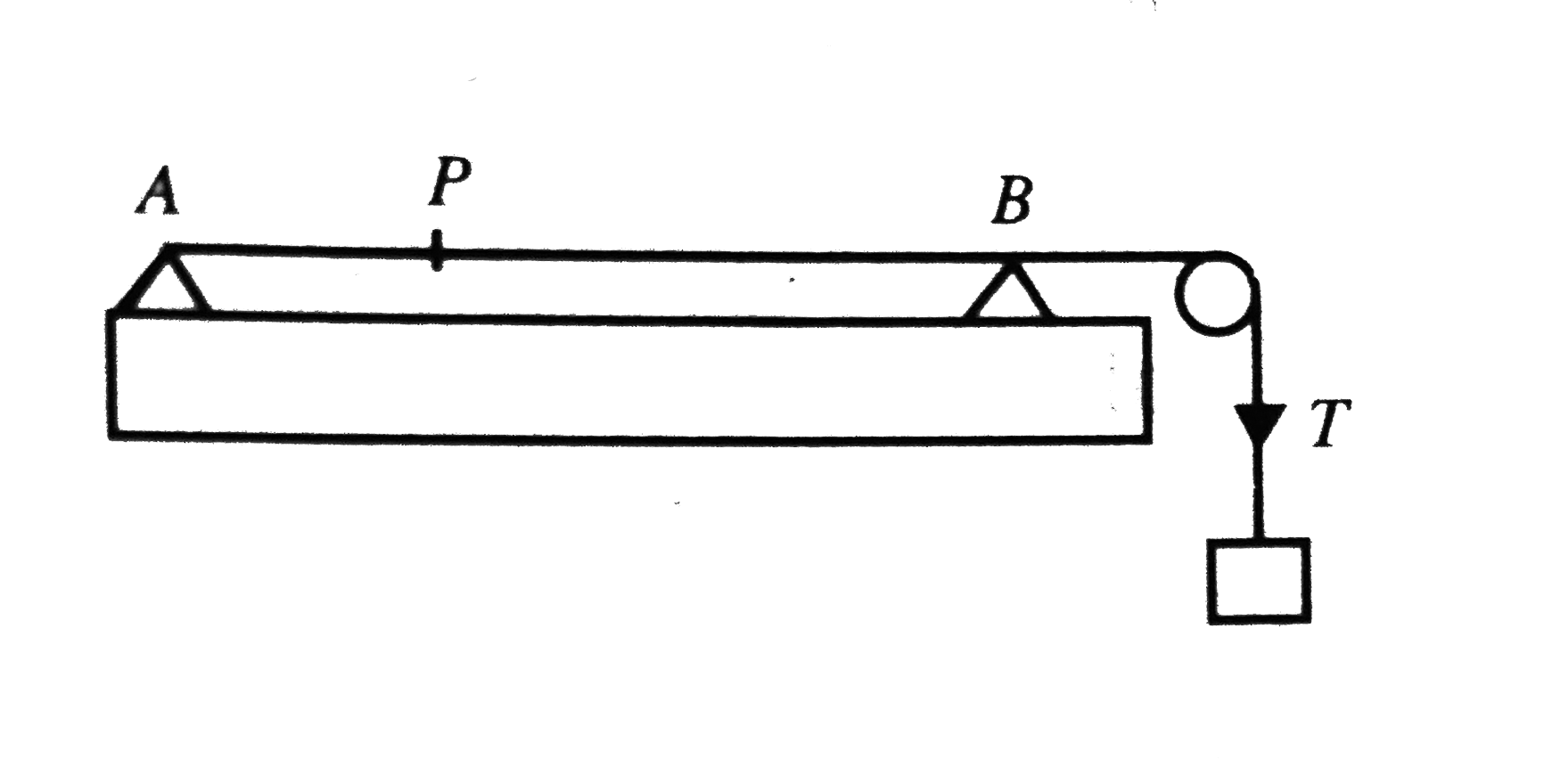
If point P is fixed so that AP:PB:1:4, then the smallest frequency for which the sonometer wire resonates is 5kHz.
If P be taken at midpoint of AB and fixed , then when the wire vibrates in the third harmonic of its fundamental , the number of nodes in the wire ( including AandB) will be totally seven.
If the fixed point P divides AB in the ratio 1:2, then the tension needed to make the string vibrate at 1kHz will be 3T. (neglecting the terminal effects)
The fundamental frequency of the sonometer wire when P divides AB in the ratio a:b will be the same as the fundamental frequency when P divides AB in the ratio b:a.
The correct Answer is:A, B, D
If P divides AB in ratio 1:4, then the fundamental frequency corresponds to 5 loops , one loop in AP and 4 loops in PB which corresponds to 5th harmonic of 1kHz. Hence fundamental =5kHz.
If P be taken at midpoint , the third harmonic will have three loops in each half of the wire AB. Hence total number of nodes (including A and B ) will be 5+2=7.
If P divides AB in the ratio 1:2, the fundamental will have three loops , corresponding to the frequency of 3kHz. For this string to vibrate with the fundamental of 1kHz , the tension must be (T/9).
The wire AB will be symmetry , vibrates with the same fundamental frequency when P divides AB in the ratio a:b or in the ratiob:a.
Topper's Solved these Questions
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:SUPERPOSITION AND STANDING WAVESExercise:Assertion - Reasoning
Explore 6 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:SUPERPOSITION AND STANDING WAVESExercise:Comprehension
Explore 55 Videos
- SUPERPOSITION AND STANDING WAVESBook:CENGAGE PHYSICS ENGLISHChapter:SUPERPOSITION AND STANDING WAVESExercise:Single Correct
Explore 144 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
- THERMODYNAMICSBook:CENGAGE PHYSICS ENGLISHChapter:THERMODYNAMICSExercise:24
Explore 1 Video
Similar Questions
A sonometer wire having a length of 1.50 m between the bridges vibrates in its second harmonic in resonance with a tuning fork of frequency 256 Hz. What is the speed of the transverse wave on the wire ?
View SolutionA sonometer wire has a total length of 1m between the fixed ends. Where should the two bridges be placed below the wire so that the three segments of the wire have their fundamental frequencies in the ratio 1 : 2 : 3 ?
View SolutionA string of length 1 m and mass 5 g is fixed at both ends. The tension in the string is 8.0 N. The string is set into vibration using an external vibrator of frequency 100 Hz. The separation between successive nodes on the string is close to :
View Solution(a) A box of weight 10√3 N is held n equilibrium with the help of two strings OA and OB as shown in figure-1. the string OA is horizontal. Find the tensions in both the stings.

(b) If you can change location of the point A on the wall and hence the orientation of the string OA without altering the orientation of the string OB as shown in figure-II. what angle should the string OA make with the wall so that a minimum tension is developed in it?
View SolutionA sonometer wire has a total length of 1 m between the fixed ends. Where should the two bridges be placed below the wire so that the three segments of the wire have their fundamental frequencies in the ratio 1 : 2 : 3 ?
View SolutionOne end of string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lowermost.point so that the string does not slack at any point in its motion along the vertical circle ?
View SolutionAn harmonic wave has been set up on a very long string which travels along the length of the string. The wave has a frequency of 50 Hz, amplitude 1 cm and wavelength 0.5 m. find
(a) the time taken by the wave to travel a distance of 8 m along the length of string (b) the time taken by a point on the string to travel a distance of 8 m, once the wave has reached the point and sets it into motion (c ) also. consider the above case when the amplitude gets doubled
View SolutionA small sphere tied to the string of length 0.8m is describing a vertical circle so that the maximum and minimum tensions in the string are in the ratio 3:1. The fixed end of the string is at a height of 5.8m above ground.
(a) Find the velocity of the sphere at the lowest position.
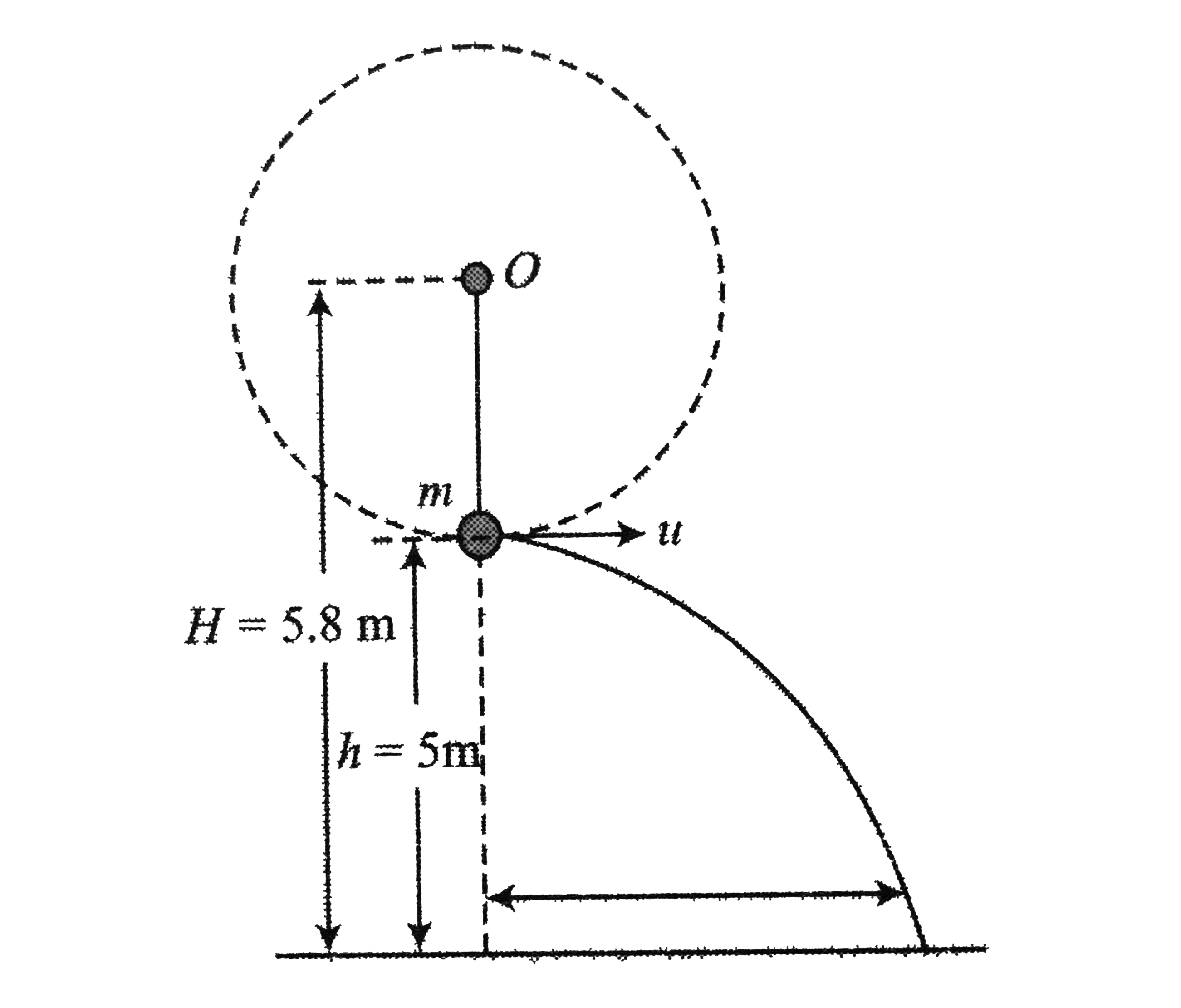
(b) If the string suddenly breaks at the lowest position, when and where will the sphere hit the ground?
View SolutionA sonometer wire has a length of 114 cm between its two fixed ends. Where should the two bridges be places so as to divide the wire into three segments, whose fundamental frequencies are in the ratio 1:3:4?
View SolutionA hollow pipe of length 0.8m is closed at one end. At its open end a 0.5m long uniform string is vibrating in its second harmonic and it resonates with the fundamental frequency of the pipe. If the tension in the wire is 50N and the speed of sound is 320ms−1, the mass of the string is
View Solution
