A source of sound is moving along a circular orbit of radius 3 m with an angular velocity of 10 rad/s. A sound detector located far away from the source is executing linear S.H.M. along the line BD (see Fig. 14.4.13) with an amplitude BC = CD=6m. The frequency of oscillation of the detector is per second. The source is at the point BA when the detector is at the point B. If the source epiits a continuous sound wave of frequency 340 Hz, find the maximum and the minimum frequencies recorded by the detector. 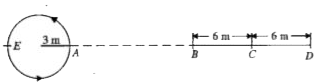
Time period of circular motion
is same as that of SHM. i.e., , so both will complete one periodic motion in same time.
Futher more, source is moving on a circle, its speed and as detector is executing
i.e., when y = 0 i.e.,detector is at C.Now in the case of Doppler effect,
So will be maximum when both move towards each other. with max i.e., the source is at M and detector at C and moving towards B, so
Similarly will be minimum when both are moving away from each other, with max i.e., the source is at N and detector at C but moving towards D,so
Topper's Solved these Questions
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - EXERCISE (LONG ANSWER QUESTIONS)
5 Videos
- WAVE MOTION AND SOUNDBOOK - AAKASH SERIESCHAPTER - WAVE MOTION AND SOUNDEXERCISE - EXERCISE (SHORT ANSWER QUESTIONS)
13 Videos
- WAVE MOTIONBOOK - AAKASH SERIESCHAPTER - WAVE MOTIONEXERCISE - PRACTICE SHEET ADVANCED (INTEGER TYPE QUESTIONS)
10 Videos
- WAVE OPTICSBOOK - AAKASH SERIESCHAPTER - WAVE OPTICSEXERCISE - PROBLEMS (LEVEL - II)
33 Videos
Similar Questions
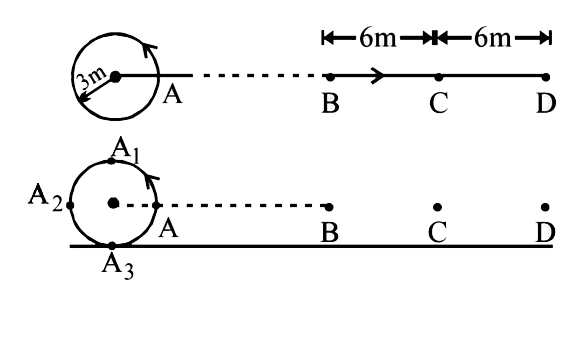
A source of sound is moving along a circular orbit of radius 3meter with an angular velocity of 10rad/s. A sound detector located far away from the source is executing linear simple harmonic motion along the line BD with an amplitude BC=CD=6meters. The frequency of oscillation of the detector is 5π per second. The source is at the point A when the detector is at the point B. If the source emits a continuous sound wave of frequency 340Hz, Find the maximum and the minimum frequencies recorded by the detector.
View SolutionA source of sound emitting a frequency 660 Hz is moving counter-clockwise in a circular path of radius 2 metres with an angular velocity 15 rad/s. A recorder at a distance from the source is moving simple harmonically along a straight line with an amplitude 2 metres. The frequency of SHM is 152π per second. The arrangement is shown in figure. When the source is at point A the detector is at D. Find the maximum and minimum frequencies recorded. Velocity of sound in air at this temperature can be taken as 300 m/s

View Solution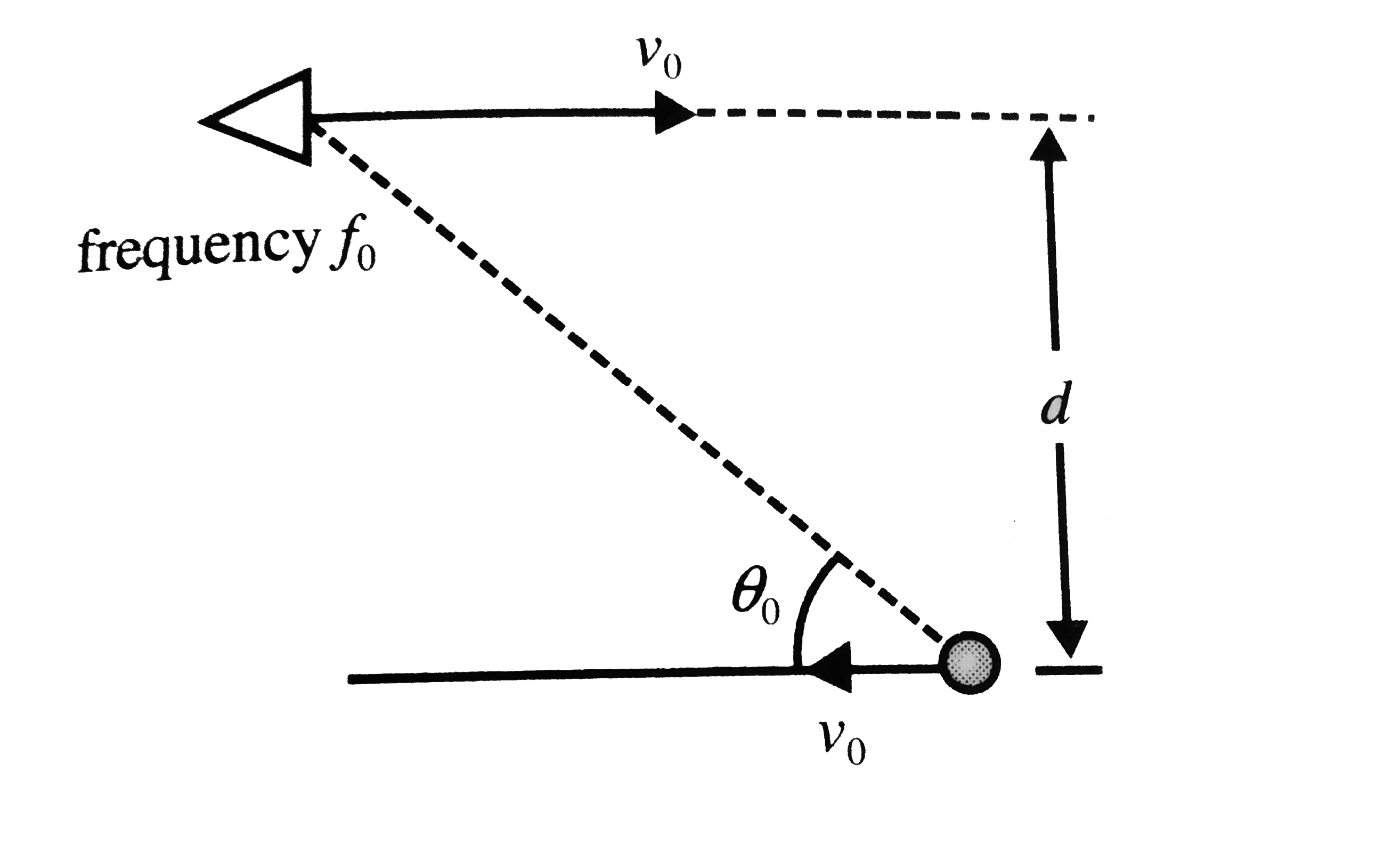
A source of sound and detector are moving as shown in Fig. at t=0. Take velocity of sound wave to be v. For this situation mark out the correct statement(s).
View Solution
A source of sound and detector are moving as shown in Fig. at t=0. Take velocity of sound wave to be v. For this situation mark out the correct statement(s).
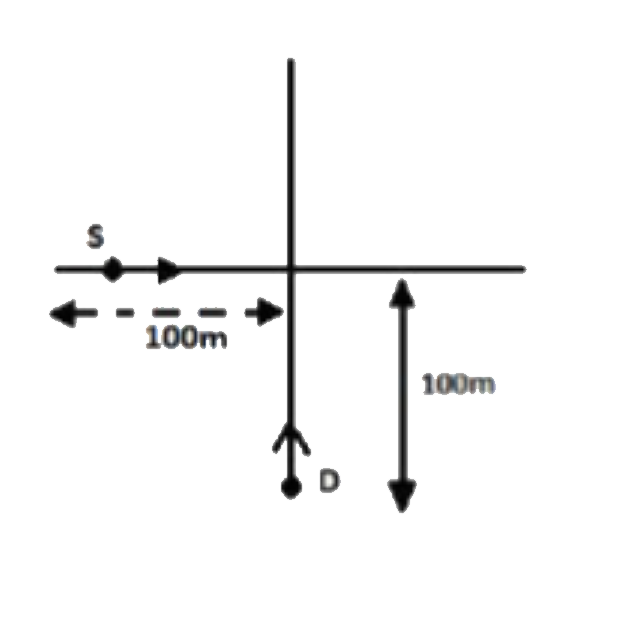
View SolutionThe figure shows the location of a source and detector at time t = 0. The source and detector are moving with velocities vs=5ˆims−1andvD=10ˆjms−1 respectively . The frequency of signals received by the detector at the moment when the source cros the origin is (the frequency of the source is 100 Hz . Velocity bof sound 330ms−1 .)
View SolutionA source of sound of frequency 500 Hz is moving towards an observer with velocity 30 m/s . The speed of sound is 330 m/s . the frequency heard by the observer will be
View SolutionA source of sound of frequency 256Hz is moving rapidly towards wall with a velocity of 5m/sec. How many beats per second will be heard if sound travels at a speed of 330m/sec.
View SolutionThe sound level at a point 5.0 m away from a point source is 40 dB. What will be the level at a point 50 m away from the source ?
View SolutionA source and a detector move away from each other, each with a speed of 10 m/s with respect to ground with no wind. If the detector detects a frequency 1650 Hz of the sound coming from the source, what is the original frequency of the source? (speed of sound = 340 m/s
View SolutionAn object is projected vertically up from the earth’s surface with velocity √Rg where R is the radius of the earth and ‘g’ is the acceleration due to earth on the surface of earth. The maximum height reached by the object is nR. Find value of n.
View Solution
