A spaceship is moving directly towards a planet at a speed of c2. When the spaceship is 4.5×108m from the planet (as measured by someone on the spaceship), a pulse of light is emitted by someone on the planet. As measured by someone on the spaceship, how long does it take the light pulse to travel from the planet to the ship?
0.5sec
1.0sec
1.5sec
2.0sec
The correct Answer is:C
The second postulate of Einstein's theory of special relativity states that the speed of light is a universal constant (c=3×108m/s), regardless of the motion of the source or the detector. So despite the fact that the spaceship is approaching the planet at a speed of c/2, occupants of the ship will still measure the speed of light to be c. the time it takes the light pulse to travel a distance of 4.5×108m is
t=dc=4.5×108m3.0×108m/s=1.5s.
Topper's Solved these Questions
Similar Questions
A spaceship is moving away from Earth at speed 0.333c. A source on the rear of the ship light at wave length 450 nm according to someone on the ship. What (a) wavelength and (b) color (blue, green, yellow, or red) are detected by someone on Earth watching the ship?
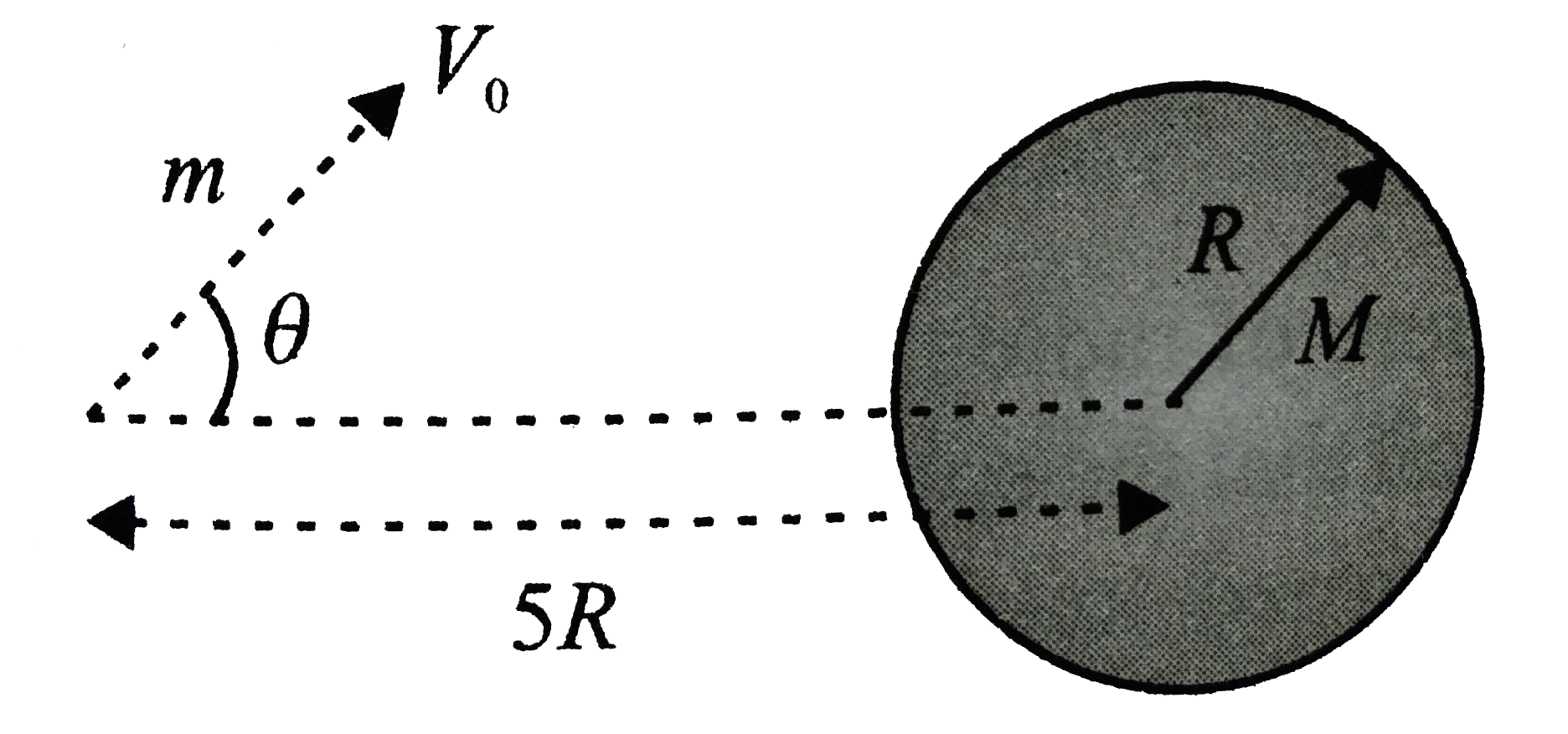
View SolutionA spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?
View Solution
Knowledge Check
A spaceship orbits around a planet at a height of 20 km from its surface. Assuming that only gravitational field of the planet acts on the spaceshop. What will be the number of complete revolutions made by the spaceship in 24 hours around the planet?
[Given mass of plane =8×1022kg
Radius of planet =2×106m
Gravitational constant G=6.67×10−11Nm2/kg2]A9B17C13D11_E01_028_Q01.png)
Spacemen Fred's spaceship (which has negligible mass) is in an elliptical orbit about planet Bob. The minimum distance between the spaceship and the planet is R, the maximum distance between the spaceship and the planet is 2R. At the point of maximum distance, spaceman fred is traveling at speed v0. he then fires his thrusters so that he enters a circular orbit of radius 2R. what is his new speed?A√3/2v0B√5v0C√3/56v0D√2v0
A spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?

View SolutionA spaceship is sent to investigate a planet of mass M and radius R. While hanging motionless in space at a distance 5R from the centre of the planet, the spaceship fires an instrument package of mass m, which is much smaller than the mass of the spaceship. For what angle θ will the package just graze the surface of the planet?

View SolutionA spaceship, moving away from Earth at a speed of 0.850c, reports back by transmitting at a frequency (measured in the spaceship frame) of 100 MHz. To what frequency must Earth receivers be tuned to receive the report?
View SolutionAn Earth starship has been sent to check an Earth outpost on the planet P1407, whose moon houses a battle group of the often hostile Reptulians. As the ship follows a straightline course first past the planet and then past the moon, it detects a high-energy microwave burst at the Reptulian moon base and then, 1.10 s later, an explosion at the Earth outpost, which is 4.00×108 m from the Reptulian base as measured from the ship's reference frame. The Reptulians have obviously attacked the Earth outpost, and so the starship begins to prepare for a confrontation with them.
The speed of the ship relative to the planet and its moon is 0.980c. What are the distance and time interval between the burst and the explosion as measured in the planet-moon frame (and thus according to the occupants of the stations)?
View SolutionA spaceship orbits around a planet at a height of 20 km from its surface. Assuming that only gravitational field of the planet acts on the spaceship, what will be the number of complete revolutiions made by the spaceship in 24 hours around the planet? [Given : Mass of Planet =8×1022kg, Radius of planet =2×106m, Gravitational constant G=6.67×10−11Nm2/kg2]
View SolutionA spaceship orbits around a planet at a height of 20 km from its surface. Assuming that only gravitational field of the planet acts on the spaceshop. What will be the number of complete revolutions made by the spaceship in 24 hours around the planet?
[Given mass of plane =8×1022kg
Radius of planet =2×106m
Gravitational constant G=6.67×10−11Nm2/kg2]
View Solution
