A spectrograph's trihedral prism is manufactured from glass whose refractive index varies with wavelength as n=A+B/λ2, where A and B are constats, with B being equal to 0.010μm2. Making use of the formula from the foregoing problem, find:
(a) how the resolving power of the prism depends on λ, calculate the value of λ/δλ in the vicinity of λ1=434nm and λ2=656nm if the width of the prism's base is b=5.0cm,
(b) the width of the prism's base capacble of resolving the yellow doublet of sodium (589.0 and 589.6nm).
λδλ=R=b∣∣∣dndλ∣∣∣=2Bb/λ3
For b=5cm,B=0.01μm2λ1=0.434μm=5×104μm
R1=1.223×104
for λ2=0.656μm
R2=0.3542×104
(b) Top resolve the D-lines we require
R=58936=982
Thus 982=0.02×b(0.5893)3
b=982×(0.5893)30.02μm=1.005×104μm=1.005cm
Topper's Solved these Questions
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Polarization Of Light
43 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Dispersion And Absorption Of Light
24 Videos
- OPTICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Interference Of Light
33 Videos
- MECHANICSBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - MECHANICSEXERCISE - Mechanics Problems
92 Videos
- OSCILLATIONS AND WAVESBOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation
36 Videos
Similar Questions
Knowledge Check
When light of wavelength λ travels through glass, the refractive index of glass varies with wavelength as μ=A+Bλ2. What are the dimensional formulae of A and B?
A[M0L0T0][M0L2T−1]B[M0L1T−1][M0L2T0]C[M0L0T0][M0L2T0]D[M1L0T1][M0L1T1]Refractive index mu is given as μ=A+Bλ2, where A and B are constants and lambda is wavelength, then dimensions of B are same as that of
AwavelengthBvolumeCpressureDareaThe refractive index of a medium is given by μ=A+Bλ2 where A and B are constants and λ is the wavelength of light.
Then the dimensions of B are the same as that ofAWavelengthBAreaCVolumeDVelocity
The refractive index μ of a medium is found to vary with wavelength λ as μ=A+Bλ2. What are the dimensions of A and B?
View SolutionShow that the area of the triangle with vertices (λ,λ−2),(λ+3,λ) and (λ+2,λ+2) is independent of λ.
View SolutionIn a single slit diffraction experiment first minima for λ1=660nm coincides with first maxima for wavelength λ2. Calculate the value of λ2.
View SolutionThe refractive index of light in glass varies with its wavelength according to equation
μ(λ)=a+bλ2 where a and b are positive constants.
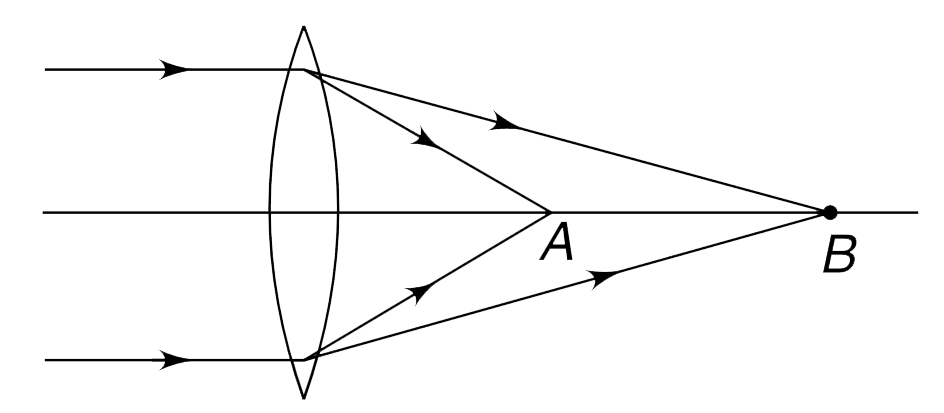
A nearly monochromatic parallel beam of light is incident on a thin convex lens as shown. The wavelength of incident light is λ0±Δλ where Δλ<<λ0. The light gets focused on the principal axis of the lens over a region AB. If the focal length of the lens for a light of wavelength λ0 is f0, find the spread AB.
View SolutionA dye absorbs a photon of wavelength λ and re− emits the same energy into two phorons of wavelengths λ1 and λ2 respectively. The wavelength λ is related with λ1 and λ2 as :
View Solution
