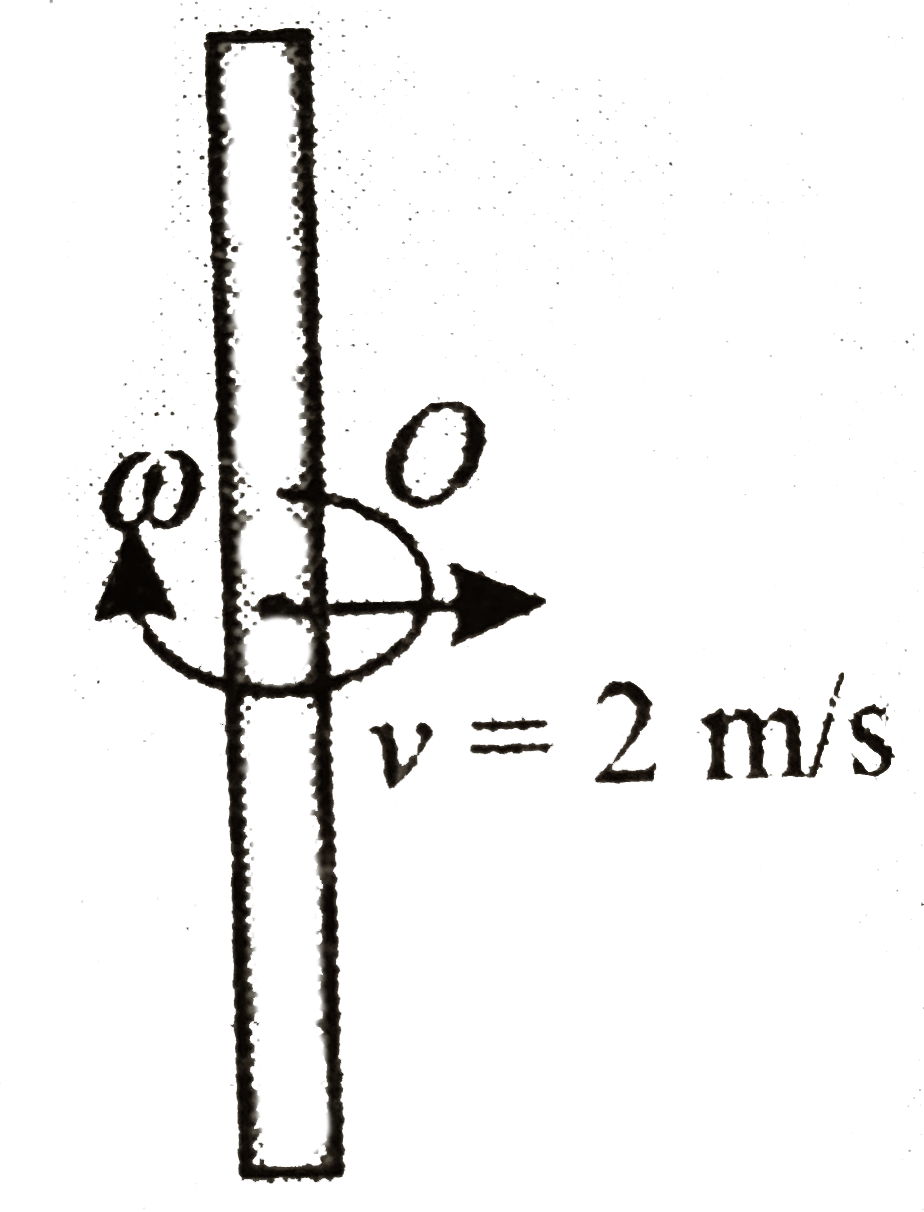A sphere is moving towards the positive x-axis with a velocity vc and rotates clockwise with angular speed ω shown in Fig. such that vc>ωR. The instantaneous axis of rotation will be
on point P
on point P'
inside the sphere
outside the sphere
The correct Answer is:D
The instantaneous axis of rotation will fall on the outside of the sphere. Since in case of pure rotation the instantaneous axis of rotation will be on the centre. In case of pure rolling, the instantaneous axis of rotationn wil be on P.
But if vC>ωR, then the instantaneous axis of rotation will fall out of the sphere.

Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Knowledge Check
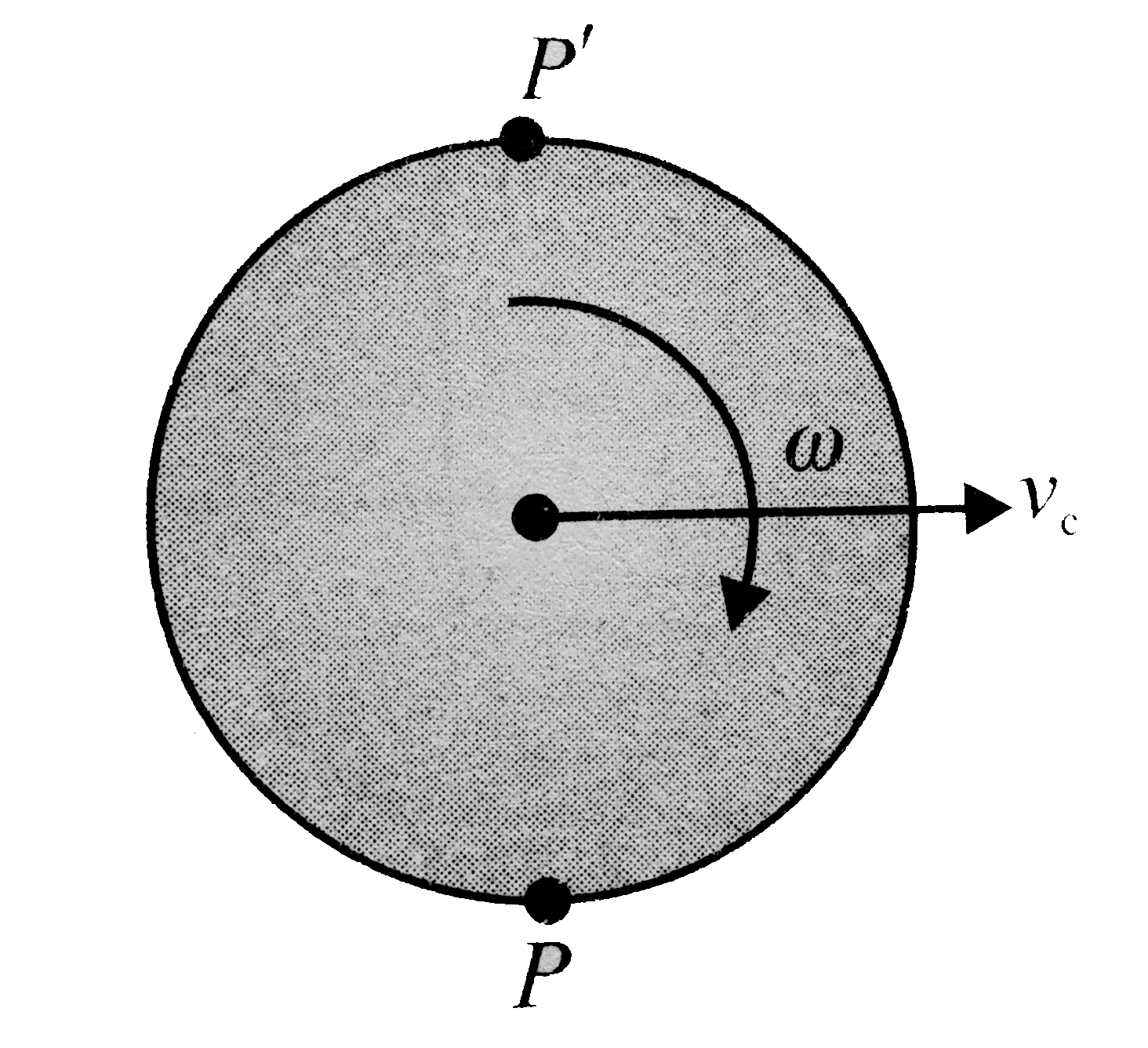
A sphere is moving at some instant with horizontal velocity v0 in right and angular velocity ω in anti clockwise sense. If |v0|=|ωR|, the instantaneous centre of rotation is
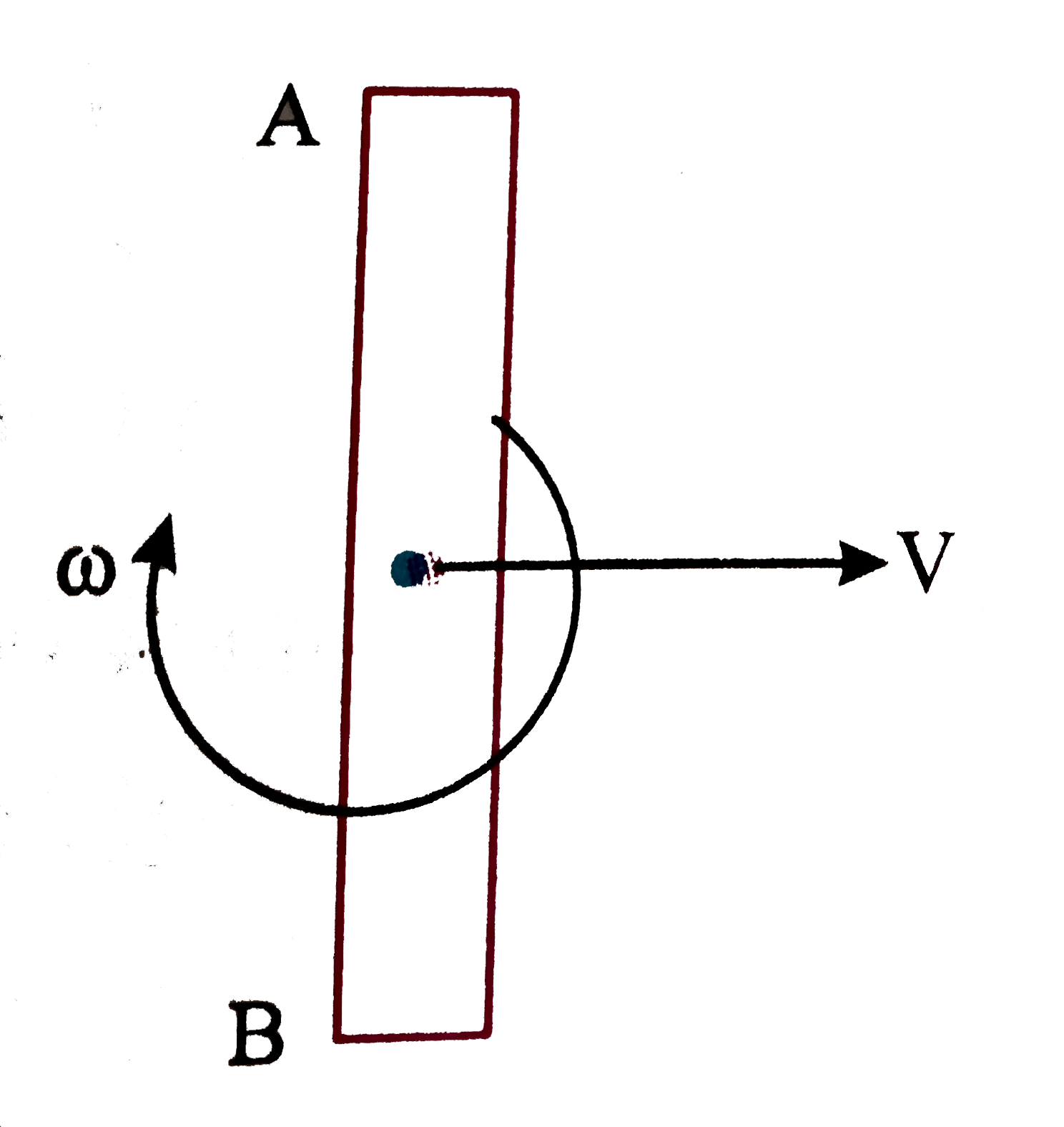
Aat the bottom of the sphereBat the top of the sphereCat the centre of the sphereDanywhere inside the sphereA rod of length l is travelling with velocity v and rotating with angular velocity ω such that ωl2=v. The distance travelled by end B of the rod when rod rotates by an angle π2 is
 A√2(2)lB52lC3lD4l
A√2(2)lB52lC3lD4lA rod is rotating with angular velocity ω about axis AB. Find cosθ.
 Ag2lω2Bglω2C2g(lω)2D3g2lω2
Ag2lω2Bglω2C2g(lω)2D3g2lω2

A disc is rolling without slipping with linear velocity v as shown in figure. With the concept of instantaneous axis of rotation, find velocities of point A, B, C and D.
View SolutionA disc is rotated about its axis with a certain angular velocity and lowered gently on a rough inclined plane as shown in Fig., then

View SolutionA sphere of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then initally
View SolutionA rod of length l is given two velocities v1 and v2 in opposite directions at its two ends at right angles to the length. The distance of the instantaneous axis of rotation from v1 is
View SolutionA rod of length l is given two velocities v1 & v2 in opposite directions at its two ends at rigt angles to the length. The distance of the instantaneous axis of rotation from v1 is:
View Solution