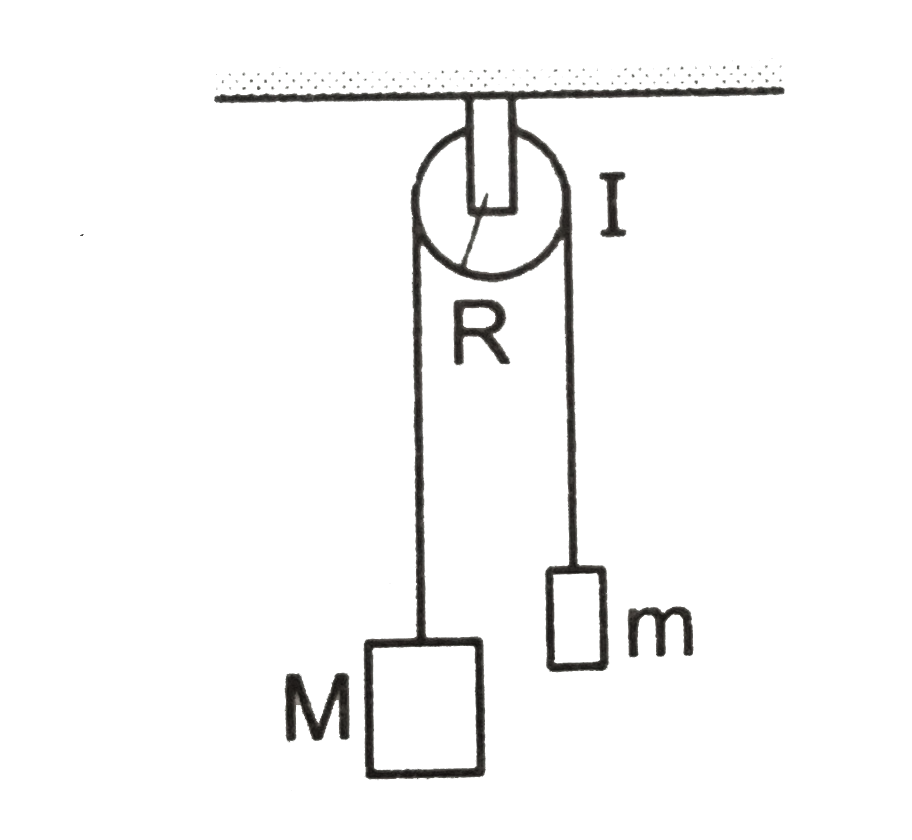
The pulleys in figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
(M−m)g(M+m+2lr2)
(M−m)g(M+m−2lr2)
(M−m)g(M+m+Ir2)
(M−m)g(M+m−Ir2)
The correct Answer is:A
T1−mg=ma ………….i
r(T2−T2)=Iα…….ii

Mg−T3=Ma………iii
r(T30−T2=Iα……….iv
and a=Rα
From eqn ii and iv we get
(M−m)g=(M+m)a=T3−T1
(M−m)g=(M−m)a+2Iar2
⇒a(M−m)g(M+m+2lr2)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct
9 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension
28 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective
13 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE
2 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
Similar Questions
Knowledge Check
The acceleration down the plane of spherical body of mass m radius R and moment of inertia I having inclination θ to the horizontal is
Agsinθ1+12/R2Bgsinθ1+I/R2Cgsinθ1+I/MR2DgsinθMR2+1A block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
Amg2m+MB2mgm+MCmgm+MD2mg2m+M
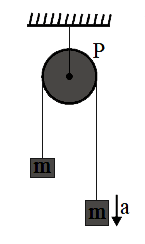
In the figure, the blocks unequal masses m1 and m2 (m1<m2).m2 has a downward acceleration a. The pulley P has a radius r, and some mass. The string does not slip on the pulley. Find the acceleration of block and angular acceleration of pulley. (I = momentum of inerita of pulley)
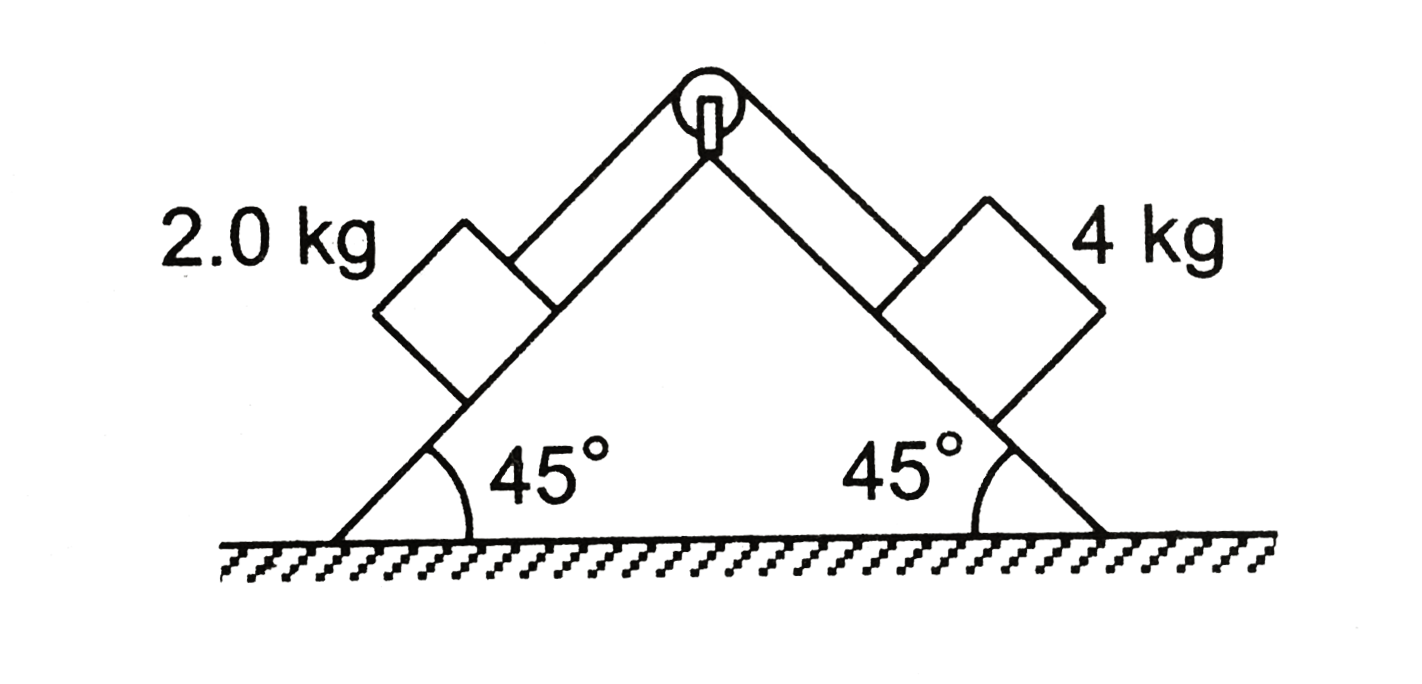
View SolutionThe pulley shown in figure has a radius 10 cm and moment of inertia 0.5 kg-m^2 about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4.0 kg block.
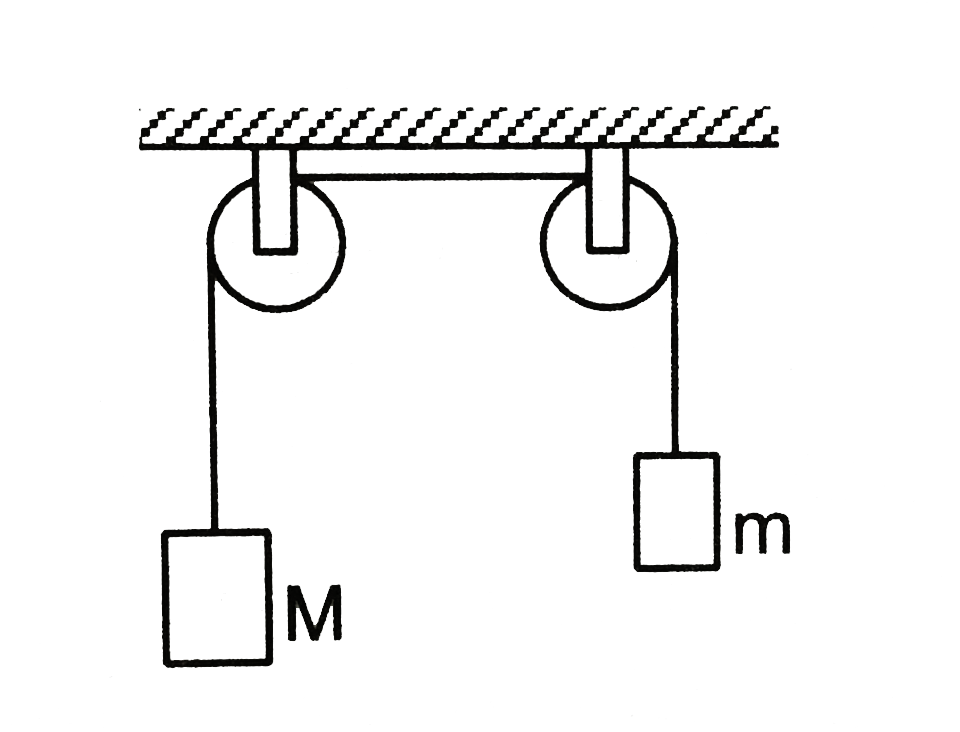
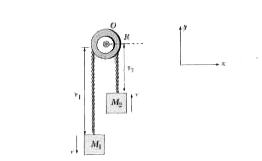
View SolutionA block of mass M1 and a block of mass M2 are connected by a string that passes over a pulley as shown in Fig. The pulley is a uniform disk of radius R and mass M. Find the acceleration of the two object, using the concepts of angular momentum and torque.
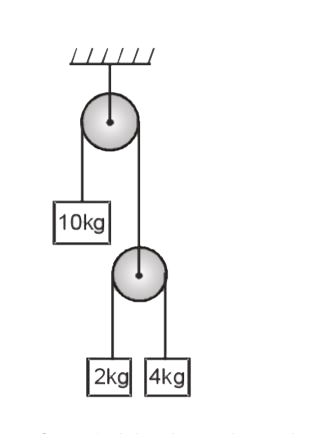
View SolutionSuppose the smaller pulley of the previous problem has its radius 5.0 cm and moment of inertia 0.10 kg-m^2. Find the tension in the part of the string joiningk the pulleys.
View SolutionThe descending pulley shown in figure has a radius 20 cm and moment of inertia 0.20 kg-m^2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1.0 kg.

View SolutionThe pulley shown in figure has a moment of inertia I about it's axis and its radius is R. Find the magnitude of the acceleration of the two blocks. Assume that the string is light and does not slip on the pulley.
View Solution