A sphere is rolling down on a sufficiently rough inclined surface.
The correct Answer is:A, B, C
When sphere tries to slip down the plane due to component of its weight along the same plane then friction acts upon the plane to oppose the possible relative motion at the contact. Friction acting this way provides necessary torque about the centre for rotational motion so that sphere may perform pure rolling. In case of pure rolling instantaneous velocity of the point of contact is zero and this is the point where friction acts hence work done by the friction remains zero and total mechanical energy remains conserved because there is no heat loss due to friction. Note that there is torque of weight of the sphere about point of contact hence angular momentum of the sphere about point of contact cannot remain constant. So options (a), (b) and (c) are correct.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
48 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A solid sphere, a hollow sphere, a solid disc and a hollow cylinder are allowed to roll down a sufficiently rough inclined plane starting from rest. All have same mass and radius.

View SolutionA solid sphere, a hollow sphere, a solid disc and a hollow cylinder are allowed to roll down a sufficiently rough inclined plane starting from rest. All have same mass and radius.

View Solution
Knowledge Check
Assertion: When a solid sphere rolls down a sufficiently rough inclined surface then its mechanical energy remains constant.
Reason: Work done by the friction in pure rolling is zero.AIf both assertion and reason are correct and reason is the correct explanation of the assertion.BIf both assertion and reason are correct but reason is not the correct explanation of assertionCIf assertion is correct but reason is incorrect.DIf assertion is incorrect but reason is correctAssertion: A sphere can perform pure rolling on a amooth surface.
Reason: When a sphere performs pure rolling on sufficiently rough surface then acceleration of point of contact is not equal to zero.AIf both assertion and reason are correct and reason is the correct explanation of the assertion.BIf both assertion and reason are correct but reason is not the correct explanation of assertionCIf assertion is correct but reason is incorrect.DIf assertion is incorrect but reason is correctA sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
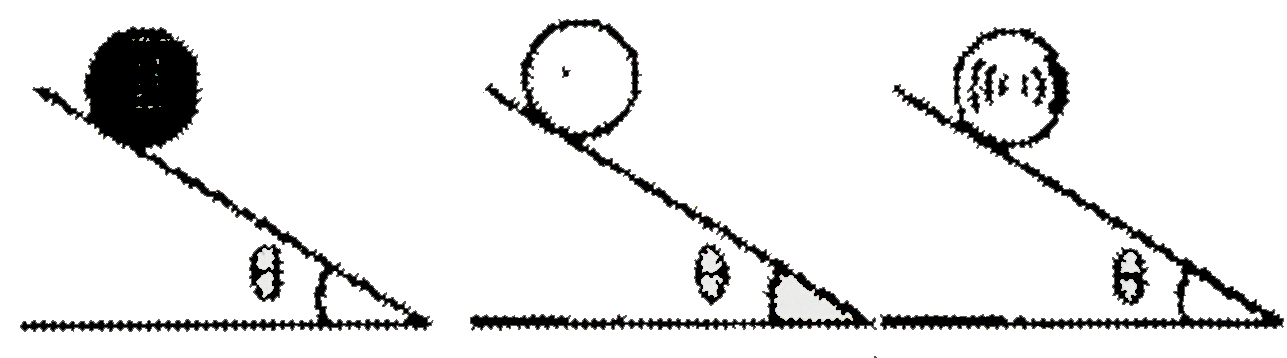
Which of the follwing order is true for final KE of the bodies?Asphere > disc > ringBring > disc > sphereCdisc > ring > sphereDdisc = ring = sphere
A solid sphere is in pure rolling motion on an inclined surface having inclination θ

View SolutionA solid sphere is in pure rolling motion on an inclined surface having inclination θ
View SolutionA sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
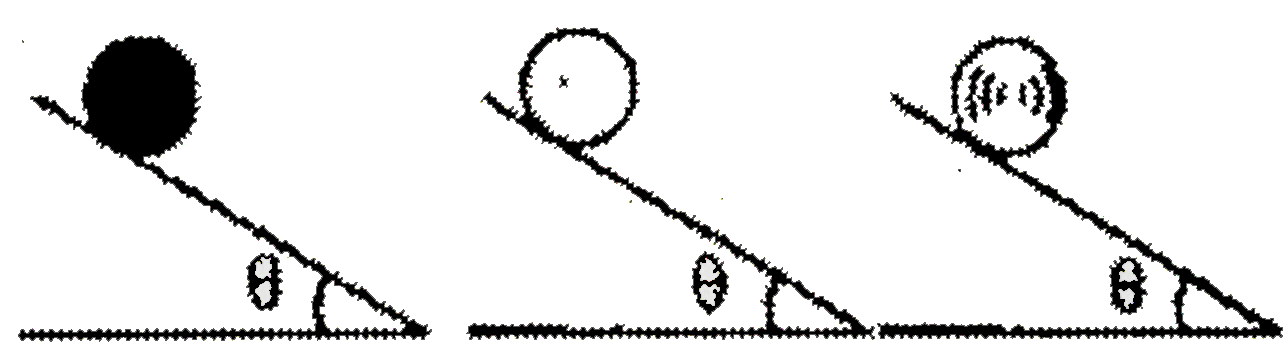
Which of the following order is true for final linear velocity of the bodies?
View SolutionA sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
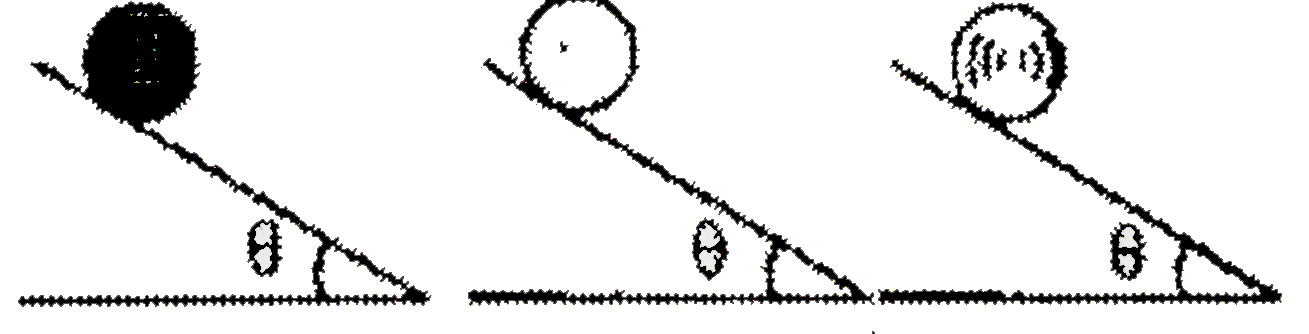
Which of the following order is true for frjctional force acting on the bodies during their rolling?
View SolutionA sphere a ring and a disc of same mass and radius are allowed to roll down three similar sufficiently rough inclined planes as shown in the figure from same height.
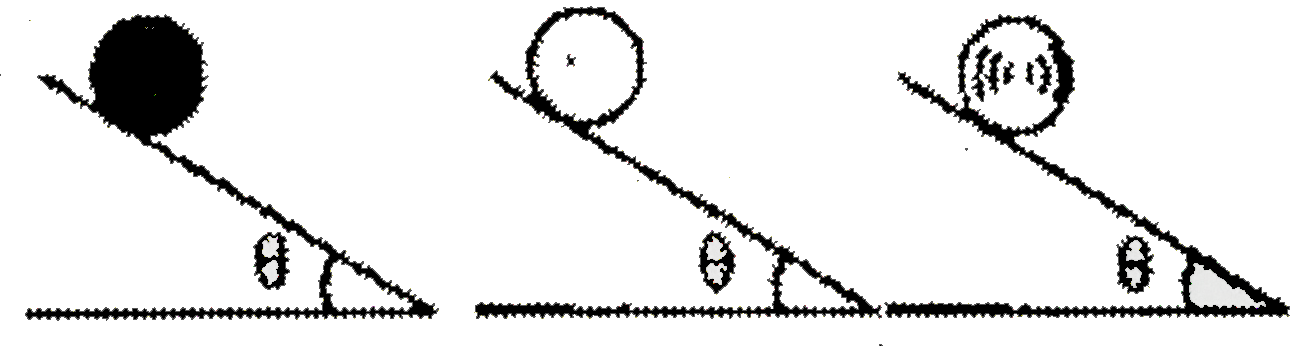
Which of the following order is' true for tiine taken by the bodies to reach the bottom of incline?
View Solution
