A solid sphere is rolled on a rough surface and it is found that sphere stops after some time.
Friction decreases the linear speed
Torque of friction tries to increase the angular speed
Torque of normal reaction tries to decrease the angular speed
Normal reaction decreases the linear speed
The correct Answer is:A, B, C
When sphere rolls on rough horizontal surface then friction acte opposite to motion and thus decreases linear speed of the sphere. But torque of friction is in the direction of angular velocity so it increases angular speed. Bodies are deformed and normal reaction gets shifted to apply torque opposite to angular velocity. This torque of normal reaction decreases angular speed. Moreover, normal reaction is vertical and cannot change linear speed. Hence options (a), (b) and (c) are correct.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
48 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
A solid sphere is rolling on a horizontal surface such that speed of the centre of sphere is u. Mase of the sphere is m and radius R. Magnitude of angular momentum about the point of contact is found to be 7nmvR/. Find the value of n
View SolutionA solid sphere rolling on a rough horizontal surface with a linear speed v collides elastically with a fixed, smooth, vertical wall. Find the speed of the sphere after it has started pure rolling in the backward direction.
View Solution
Knowledge Check
A solid sphere is rolling on a rough surface, whose centre of mass is at C at a certain instant. Find at that instant it has angular velocity ω. Its radius is R. Find the angular acceleration at that instant mass of sphere is m
 A52gdR2B57gdR2C52d(g+ω2R)R2D57d(g+ω2R)R2
A52gdR2B57gdR2C52d(g+ω2R)R2D57d(g+ω2R)R2A solid sphere rolling on a rough horizontal surface. Acceleration of contact point is zero.
A solid sphere can roll on the smooth surface.AStatement-1 is True, Statement-2 is Ture , Statement -2 is a correct explanation for statement -1.BStatement-1 is True, Statement-2 is True , Statement-2 is NOT a correct explanation fro Statement -1.CStatement-1 is True, Statement-2 is False.DStatement-1 is False, Statement-2 is True.A solid sphere is rolling without slipping on a level surface dat a constant speed of 2.0ms−1 How far can it roll up a 30∘ ramp before it stops ?
A56 cmB26 cmC53 cmD84 cm
A sphere is rolled on a rough horizontal surface. It gradually slows down and stops. The force of friction tries to
View SolutionA solid sphere is thrown on a horizontal rough surface with initial velocity of centre of mass V0 without rolling. Velocity of its centre of mass when its starts pure rolling is
View SolutionA solid sphere rolls on a smooth horizontal surface at 10m/s and then rolls up a smooth inclined plane of inclination 30∘ with horizontal. The mass of the sphere is 2kg. Find the height attained by the sphere before it stops (in m).
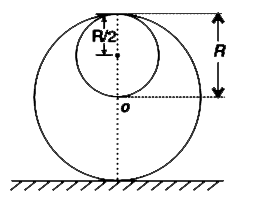
View SolutionA spherical cavity of radiusR2 is removed from a solid sphere of radius R as shown in fig. The sphere is placed on a rough horizontal surface as shown. The sphere is given a gentle push. Friction is large enough to prevent slippage. Prove that the sphere perform SHM and find the time period.
View SolutionA solid sphere rolls on horizontal surface without slipping. What is the ratio of its rotational to translation kinetic energy.
View Solution
