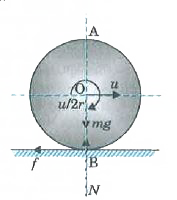
State of the sphere at some instant of time is shown in figure. Surface below the sphere is rough. At the given instant, speed of the centre of the sphere is u and angular velocity about the centre is u/2r. Select correct statement (s)
Direction of friction on the sphere is towards left
Direction of friction on the sphere is towards right
Angular momentum about point o remains conserved
Angular momentum about point B remains conserved
The correct Answer is:A, D
Forces acting on the sphere are as shown in figure.
Velocity of the bottom point B due to translation is u towards right and due to rotation it is u/2 towards left. Hence net velocity of the bottom point is towards right. So we can understand that friction will act towards eft in order to oppose this relative motion. Option (a) is correct whereas (b) is wrong.
Further we can see that friction is applying torque about the centre O hence angular momentum about the centre will not remain conserved. Hence option (c) is wrong
All the forces are passing through the point B hence there is no torque about this point. So angular momentum about the point B remains conserved. Option (d) is also correct.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE (OBJECTIVE TYPE QUESTIONS (ASSERTION REASON TYPE QUESTIONS) )
10 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (MATCHING TYPE QUESTIONS) )
3 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - MODERN PUBLICATIONCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - COMPETITION FILE ( OBJECTIVE TYPE QUESTIONS (JEE (Main) & Other State Boards for Engineering Entrance) )
48 Videos
- PHYSICAL WORLD BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)
6 Videos
- THERMAL PROPERTIES OF MATTERBOOK - MODERN PUBLICATIONCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Knowledge Check
An electric dipole is placed at the centre of a sphere. Select the correct alternative(s).
AThe flux of electric field through the sphere is zeroBThe electric field is zero at every point of the sphereCThe electric field is not zero anywhere on the sphereDThe electric field is zero on a circle on the sphere
System is shown in the figure. Velocity of sphere A is 9 ms. Find the speed of sphere B.A9msB12msC9×54msDnone of theseState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.

What will be the speed of sphere when it starts pure rolling?A4u7B3u7C2u7Du7
A solid sphere is given an angular velocity ω and kept on a rough fixed incline plane. The choose the correct statement.

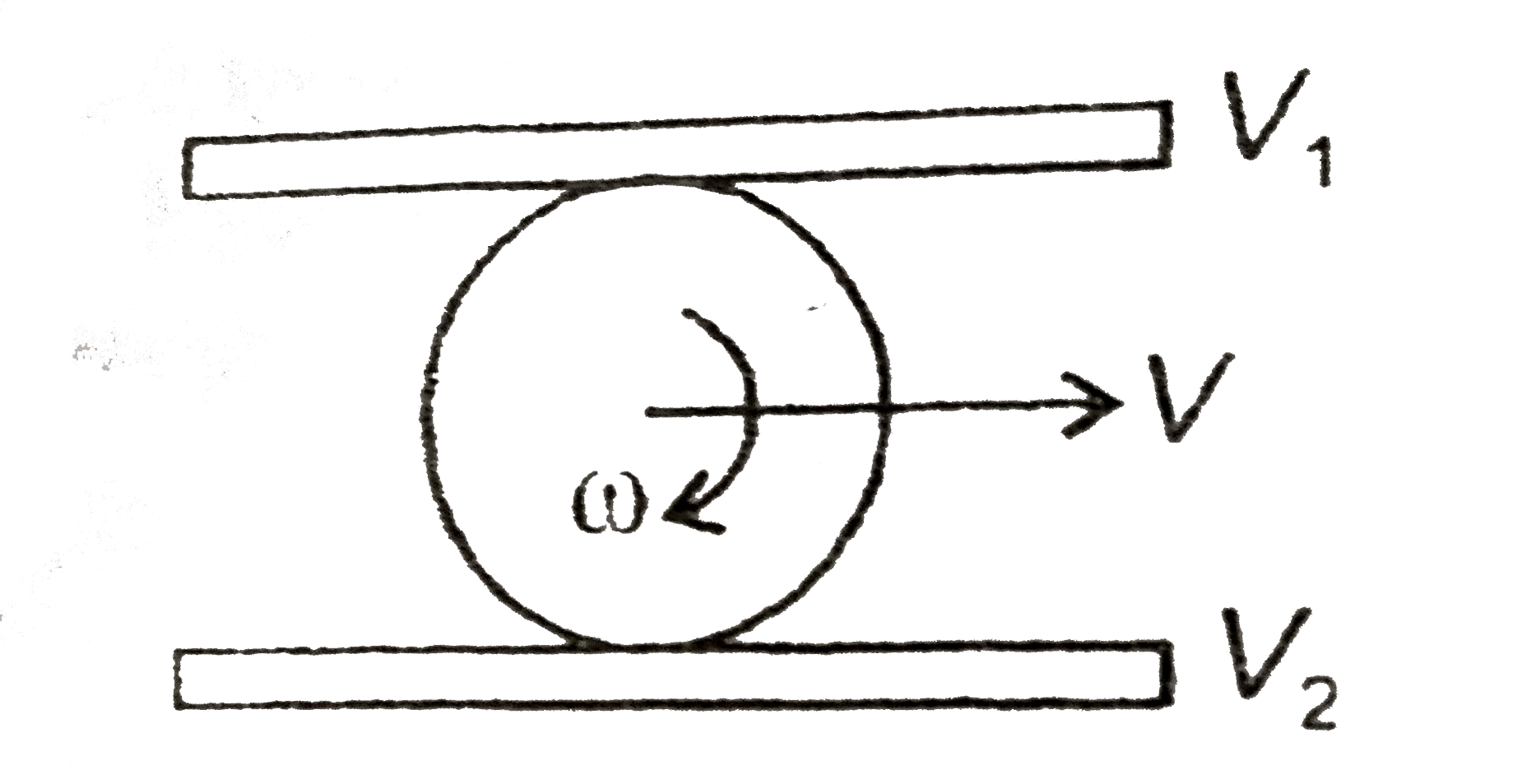
View SolutionA sphere of radius R rolls without slipping between two planks as shown in figure. Find
(a) Speed of centre of sphere
(b) Angular velocity of the sphere
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here r is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assuming coefficient of friction between sphere and the surface. Mass of sphere is m.
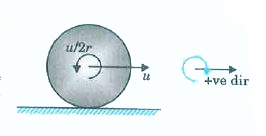
At what time sphere stops rotating for a moment?
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.
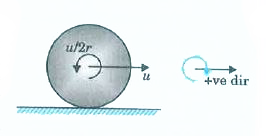
At what time sphere starts pure rolling?
View SolutionA solid sphere is given an angular velocity ζ and kept on a rough fixed incline plane. The choose the correct statement.

View Solution
