A sphere of mass $0.1 k g$ is attached to an inextensible string of length $1.3 m$ whose upper end is fixed to the ceilling The sphere is made to describe a horizontal circle of radius $0.5 m$ Calculate time period of revolution and tension in the string .

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $2.2 s; 1.06 N$ .

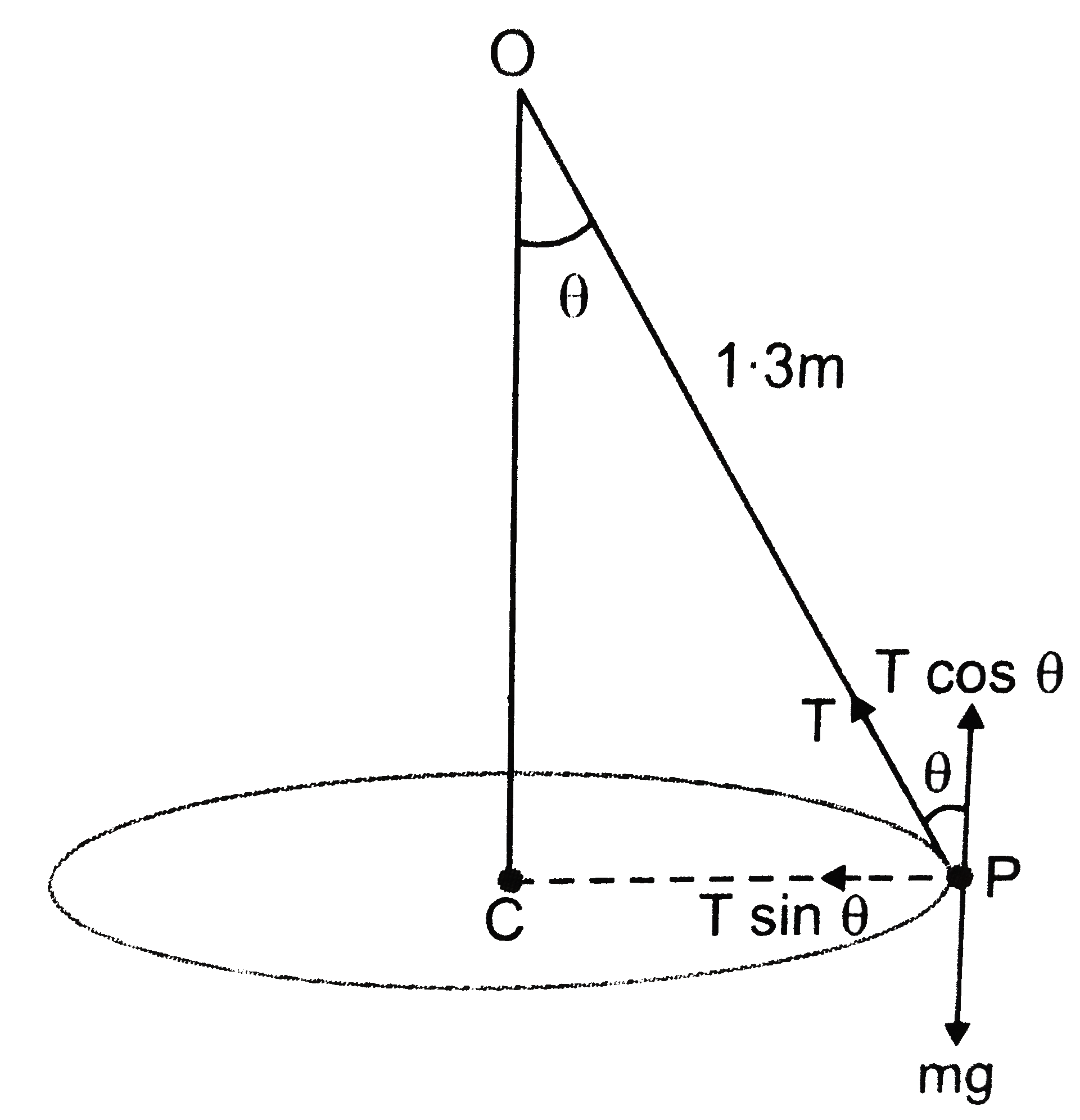
Here, $m = 0.1 k g, O P = l = 1.3 m, C P = r = 0.5 m$
time period $t = ?$ tension $T = ?$
$sin θ = \frac{r}{t} = \frac{0.5}{1.3} = 0.3846$
$θ = {sin}^{- 1} (0.3846) = {22.62}^{\circ}$
As is clear from
$T cos θ = m g$
$T = \frac{m g}{cos θ} = \frac{0.1 \times 9.8}{{cos 22.62}^{\circ}} = \frac{0.98}{0.9231} = 1.06 N$
Also $T sin θ = m r ω^{2} = \frac{m r 4 π^{2}}{t^{2}}$
$∴ t^{2} = \frac{4 π^{2} m r}{T sin θ}$
$= 4 \times \frac{22}{7} \times \frac{22}{7} \times \frac{0.1 \times 0.5}{1.06 \times 0.3846} = 4.846$
$t = \sqrt{4.846} = 2.2 s$
.

|

Updated on:21/07/2023

Class 11 PHYSICS NEWTONS LAW OF MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass 200 g is attached to an ideal string of length 1.30 m whose upper end is fixed to ceiling. The particle is made to revolve in a horizontal circle of radius 50 cm. The tension in the string is (g = 10 m/ $s^{2}$ )
A $\frac{13}{6} N$
B $\frac{11}{6} N$
C $\frac{26}{5} N$
DZero
Question 2 - Select One

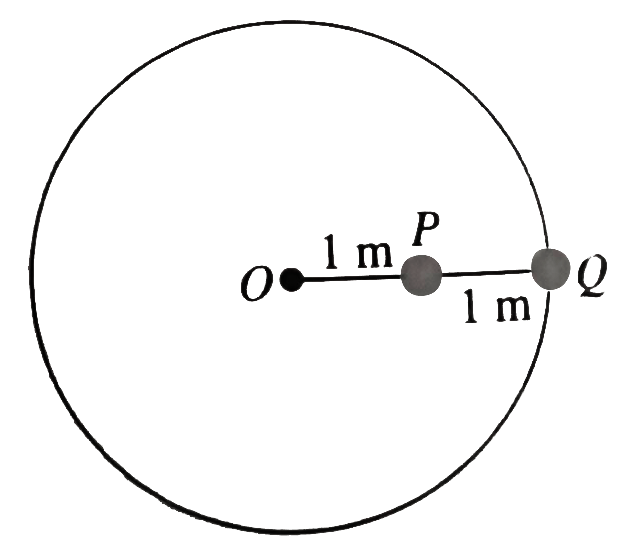
Two spheres of equal masses are attached to a string of length 2 m as shown in figure. The string and the spheres are then whirled in a horizontal circle about O at a constant rate. What is the value of the ratio:
A $\frac{1}{2}$
B $\frac{2}{3}$
C $\frac{3}{2}$
D2
Question 3 - Select One
A stone of mass $1 / 2$ kg is whriled round the end of a piece of string in a horizontal circle of radius half a meter with a uniform speed of $1 m / s$ . The tension in the string is
A $25 \times 10^{3}$ dynes
B $10^{5}$ dynes
C $5 \times 10^{4}$ dynes
D $4 \times 10^{5}$ dynes

PRADEEP-LAWS OF MOTION-Problems for practice

Home
Ask Doubt
Profile