A spinning cylinder with angular velocity ω0 of mass M and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1/√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
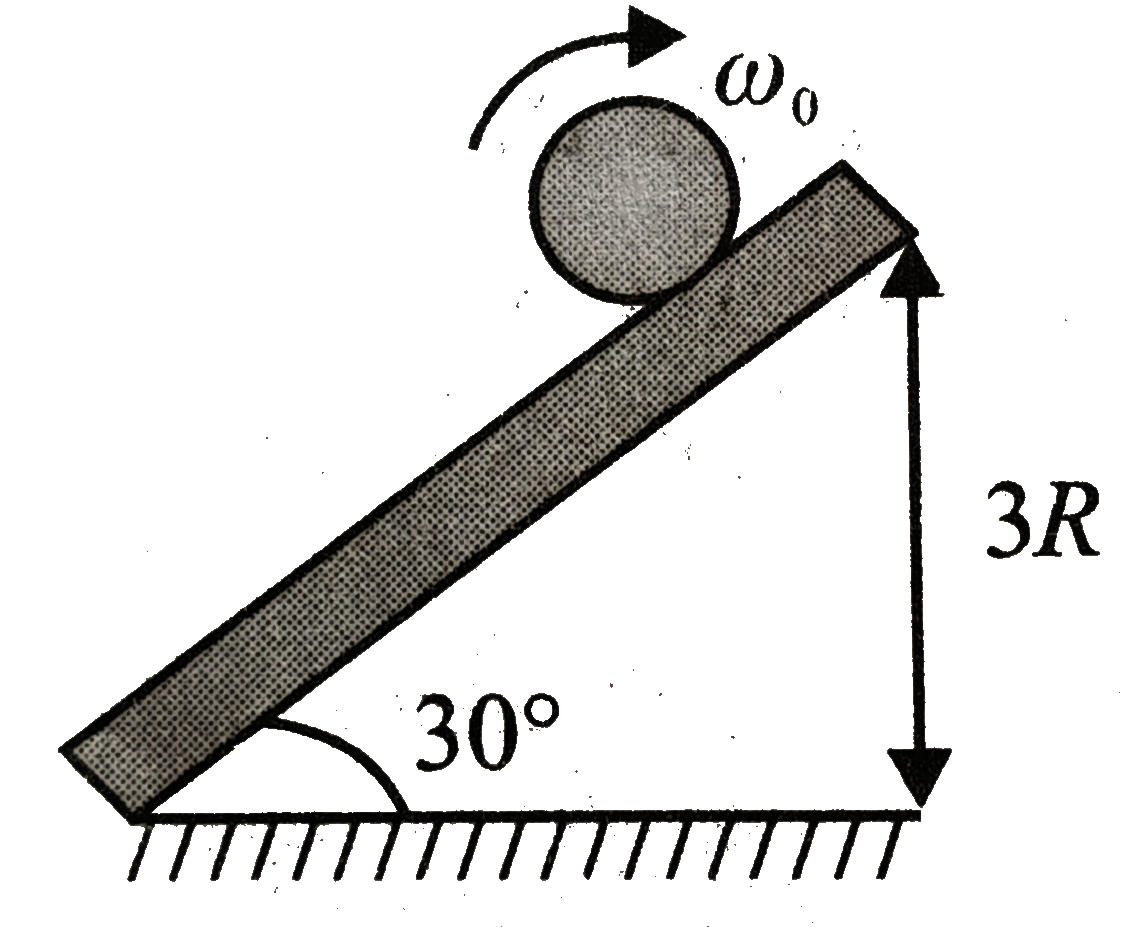
The correct Answer is:√Rg
We will check whether the cylinder slips down the incline or not
As mgsin30∘=μmgcos30∘ initially the cylinder slips at its place till the angular velocity becomes zero.
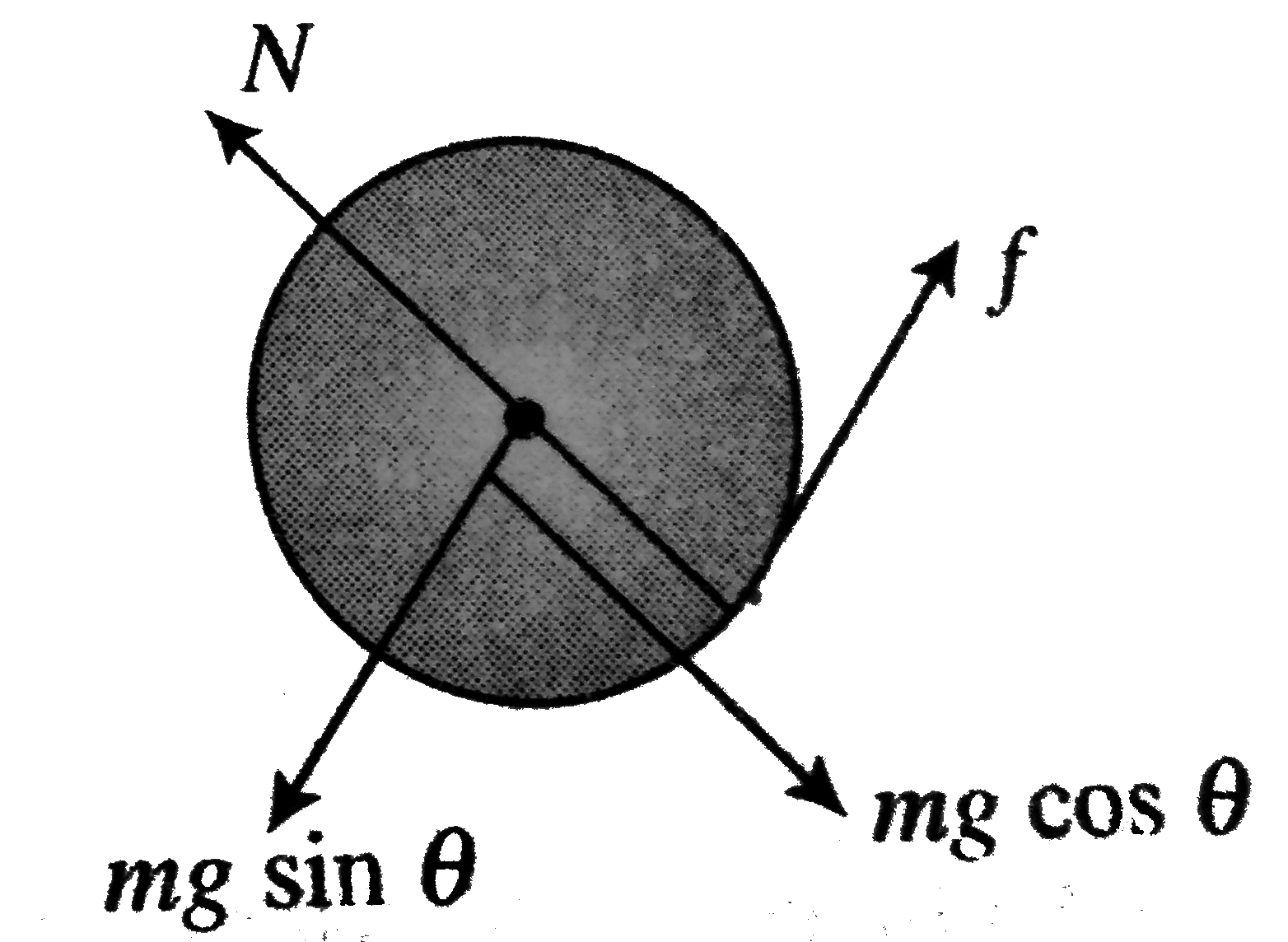
Στ=(μmgcosθ)R=mR22α
α=2μcosθRg
0=ω0−α1 or t1=ω0α
Next the sphere will come down with initial angular and linear velocity both zero.
fR=mR22α⇒f=mRα2
and mgsinθ−f=ma
If pure rolling takes place a=Rα.
⇒2f=ma
mgsiθ=3f
f=13mgsinθ⇒f=16mg
As fmax=μmcosθ=1√3mg×√32=mg2
and fmax<f so pure rolling is possible.
a=2fm=2(mg/6)mm=g3
Let t2 be the time taken to reach the foot of the incline.
3Rsin30∘=12g3t22 or t2=6√R6
Hence total time t=t1+t2(ω0Rg+6√Rg)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Single Correct
142 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct
26 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A spinning cylinder of mass m and radius R is lowered on a rough inclined plane of angle 30∘ with the horizontal and μ=1√3. The cylinder is released at a height of 3R from horizontal. Find the total time taken by the cylinder to reach the bottom of the incline.
View SolutionA solid cylinder of mass 8 kg and radius 50 cm is rolling down a plane inclined at an angle of 30∘ with the horizontal. force of friction on the cylinder is?
View Solution
Knowledge Check
A cylinder of mass M and radius R rolls on an inclined plane. The gain in kinetic energy is
A12Mv2B12Iω2C34Mv2D34Iω2A cylinder of mass M and radius R rolls on an inclined plane. The gain in kinetic energy is
A12Mv2B12Iω2C34Mv2D34Iω2A ring of mass m and radius R is rolling down on a rough inclined plane of angle θ with horizontal. Plot the angular momentum of the ring about the point of contact of ring and the plane as a function of time
A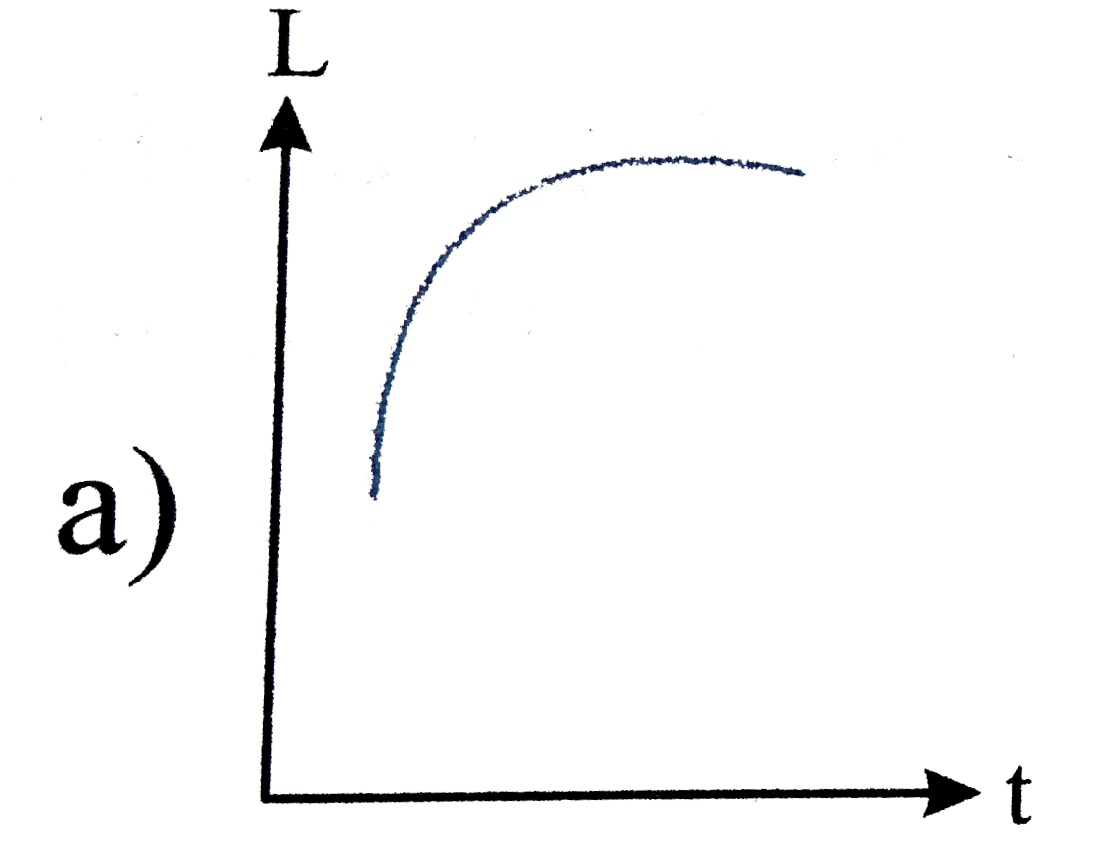 B
B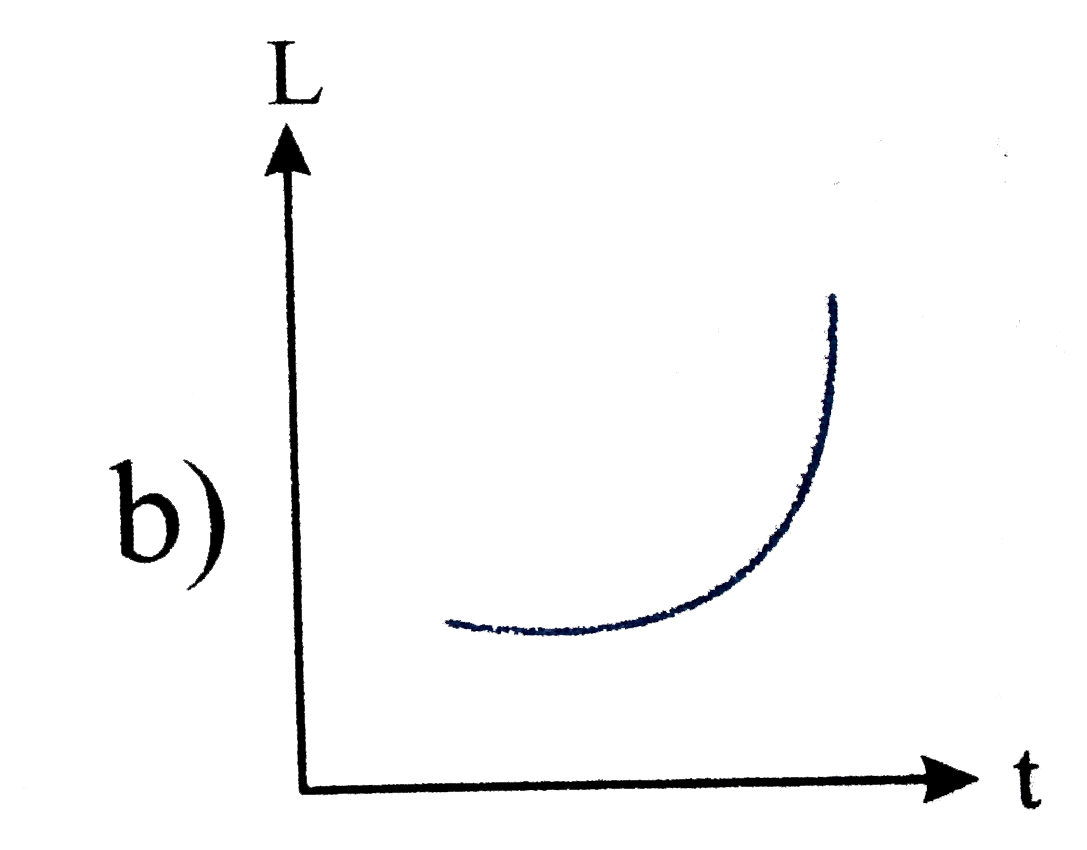 C
C D
D
If the body starts from rest from the top of the rough inclined plane of length 1, time taken to reach the bottom of the plane is
View SolutionA solid cylinder of mass M and radius R rolls without slipping down an inclined plane making an angle 6 with the horizontal. Then its acceleration is.
View SolutionA solid cylinder rolls down from an inclined plane of height h. What is the velocity of the cylinder when it reaches at the bottom of the plane ?
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View Solution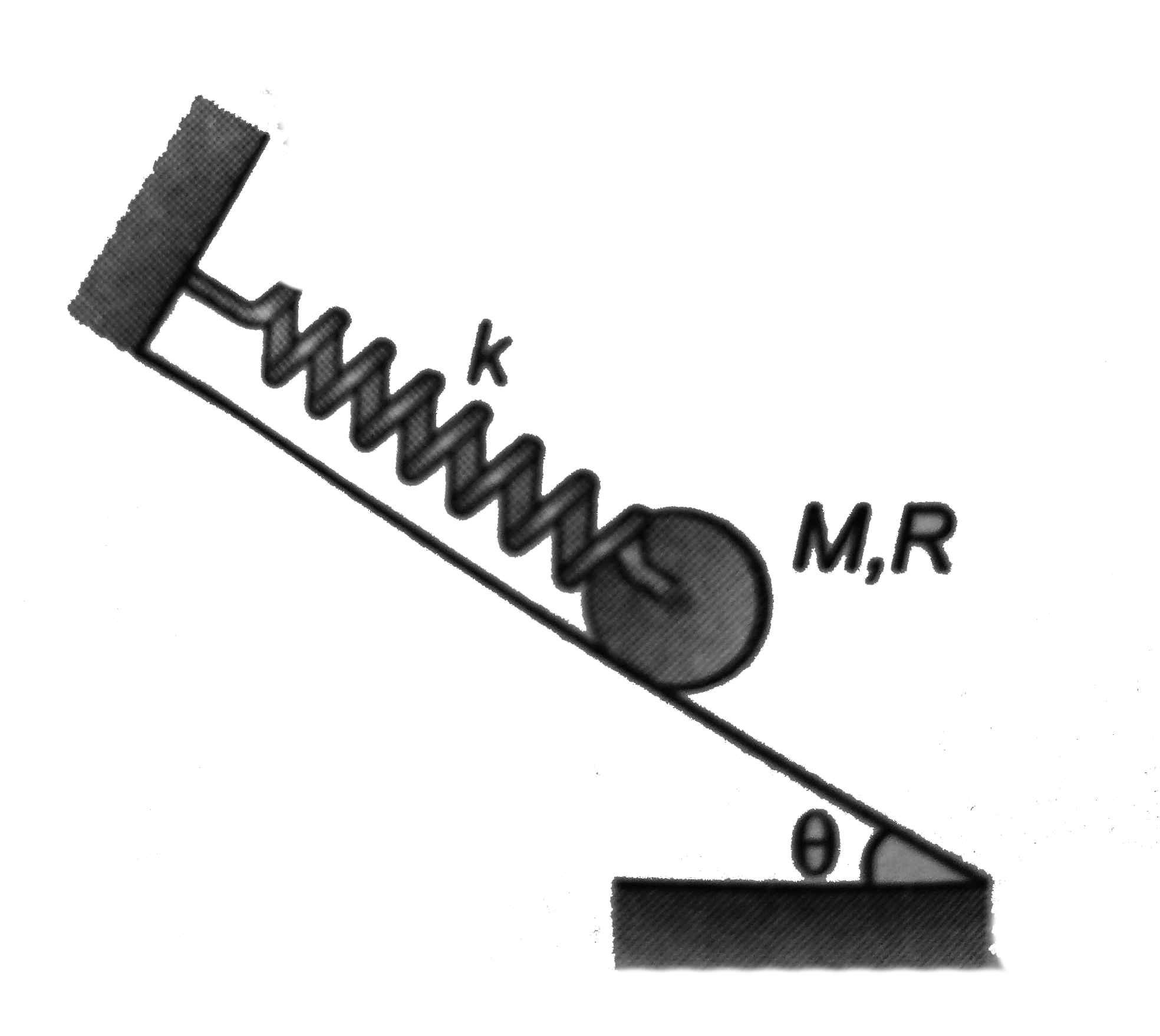
A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k is
View Solution
