A spring and block are in the arrangement of Fig. 8-12. When the block is pulled out to x=+4.0cm, we must apply a force of magnitude 360 N to hold it there. We pull the block to x=11 cm and then release it. How much work does the spring do on the block as the block moves from xi=+5.0cm to (a) x=+3.0cm, (b) x=3.0cm, (c) x=−5.0cm, and (d) x=−9.0cm ?
The correct Answer is:(a) 7.2 J ; (b) 7.2 J ; (c) 0 J ; (d) -25 J
To solve the problem, we need to calculate the work done by the spring on the block as it moves from an initial position xi to a final position xf. The work done by the spring can be calculated using the formula:
W=−12k(x2f−x2i)
Where:
- W is the work done by the spring,
- k is the spring constant,
- xi is the initial position,
- xf is the final position.
Step 1: Determine the Spring Constant k
From the information given, when the block is pulled to x=+4.0cm and held there, a force of 360N is required. The spring force is given by:
F=kx
Where x=0.04m (since 4.0cm=0.04m). Rearranging gives:
k=Fx=360N0.04m=9000N/m
Step 2: Calculate Work Done for Each Case
(a) From xi=+5.0cm to xf=+3.0cm
Convert cm to m:
- xi=0.05m
- xf=0.03m
Now, substitute into the work formula:
W=−12⋅9000⋅(0.032−0.052)
Calculating the squares:
W=−12⋅9000⋅(0.0009−0.0025)=−12⋅9000⋅(−0.0016)=7.2J
(b) From xi=+5.0cm to xf=−3.0cm
Convert cm to m:
- xf=−0.03m
Now substitute into the work formula:
W=−12⋅9000⋅((−0.03)2−(0.05)2)
Calculating:
W=−12⋅9000⋅(0.0009−0.0025)=−12⋅9000⋅(−0.0016)=7.2J
(c) From xi=+5.0cm to xf=−5.0cm
Convert cm to m:
- xf=−0.05m
Now substitute into the work formula:
W=−12⋅9000⋅((−0.05)2−(0.05)2)
Calculating:
W=−12⋅9000⋅(0.0025−0.0025)=0J
(d) From xi=+5.0cm to xf=−9.0cm
Convert cm to m:
- xf=−0.09m
Now substitute into the work formula:
W=−12⋅9000⋅((−0.09)2−(0.05)2)
Calculating:
W=−12⋅9000⋅(0.0081−0.0025)=−12⋅9000⋅0.0056=−25.2J
Summary of Work Done
- (a) W=7.2J
- (b) W=7.2J
- (c) W=0J
- (d) W=−25.2J
- W is the work done by the spring,
- k is the spring constant,
- xi is the initial position,
- xf is the final position.
- xi=0.05m
- xf=0.03m
- xf=−0.03m
- xf=−0.05m
- xf=−0.09m
- (a) W=7.2J
- (b) W=7.2J
- (c) W=0J
- (d) W=−25.2J
Topper's Solved these Questions
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (Single Correct Choice Type)
59 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - PRACTICE QUESTIONS (More than one choice correct type)
10 Videos
- WORK, POWER, AND ENERGYBOOK - RESNICK AND HALLIDAYCHAPTER - WORK, POWER, AND ENERGYEXERCISE - CHECKPOINT
6 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A 10−kg block moves in a straight line under the action of a force that varies with position as shown in figure. How much work does the force do as the block moves from origin to x=8m?
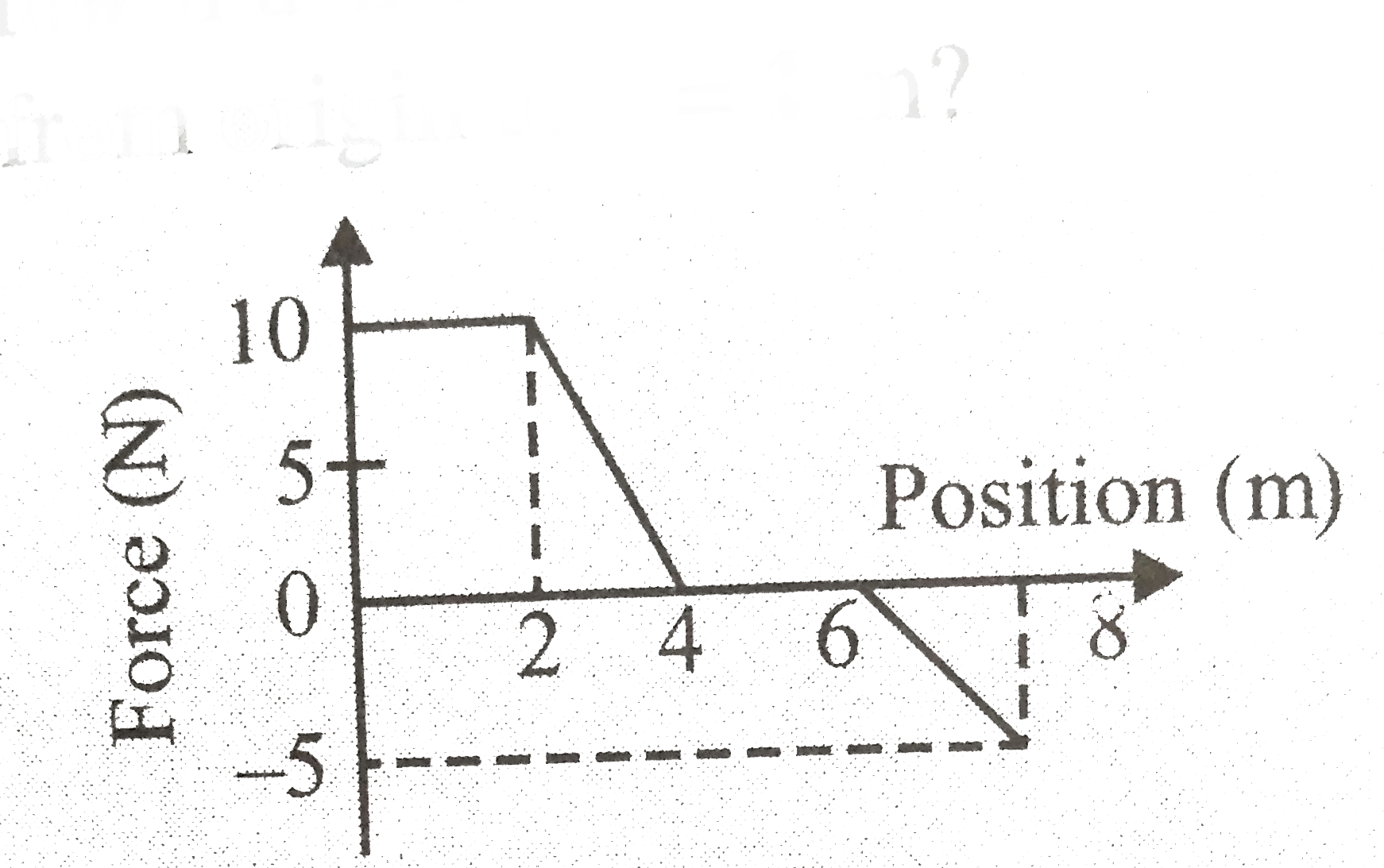
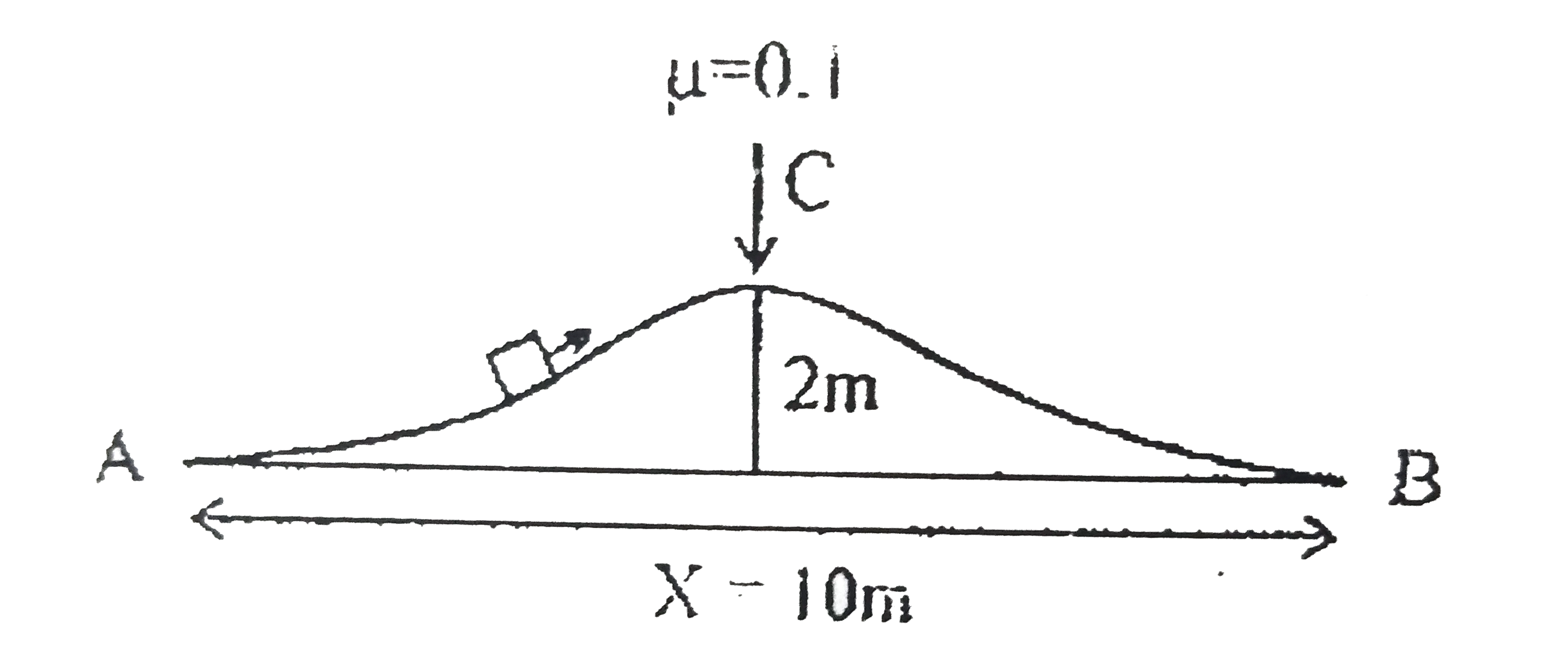
View SolutionA block of mass 0.4kg is pulled along the curve path CAN slowly by a tangential force as shown in figure. The work done by the applied force when the block moves from A to B is
View Solution
Knowledge Check
A spring block system is placed on a rough horizontal floor. The block is pulled towards right to give spring some elongation and released.
 AThe block may stop before the spring attains its natural lengthBThe block must stop with spring having some comprission.CThe block may stop with spring having some compression.DIt is not possible that the block stops at antural length of the spring.
AThe block may stop before the spring attains its natural lengthBThe block must stop with spring having some comprission.CThe block may stop with spring having some compression.DIt is not possible that the block stops at antural length of the spring.A spring block system is placed on a rough horizontal floor. The block is pulled towards right to gives spring some elongation and released, Then :
 Athe block may stop before the spring attains its natural lengthBthe block must stop with spring having some compressionCthe block may stop with spring having sme compressionDit is not possible that the block stops at mean position
Athe block may stop before the spring attains its natural lengthBthe block must stop with spring having some compressionCthe block may stop with spring having sme compressionDit is not possible that the block stops at mean positionA block of mass 0.1 is held against a wall applying a horizontal force of 5N on block. If the coefficient of friction between the block and the wall is 0.5, the magnitude of the frictional force acting on the block is:
A2.5NB0.98NC4.9ND0.49N
A 100g block moves along X− axis. Its acceleration as a function of displacemetn is shown in figure. Calculate work done (in joule) on the block by the force applied as the block moves from x=0 to x=8m.

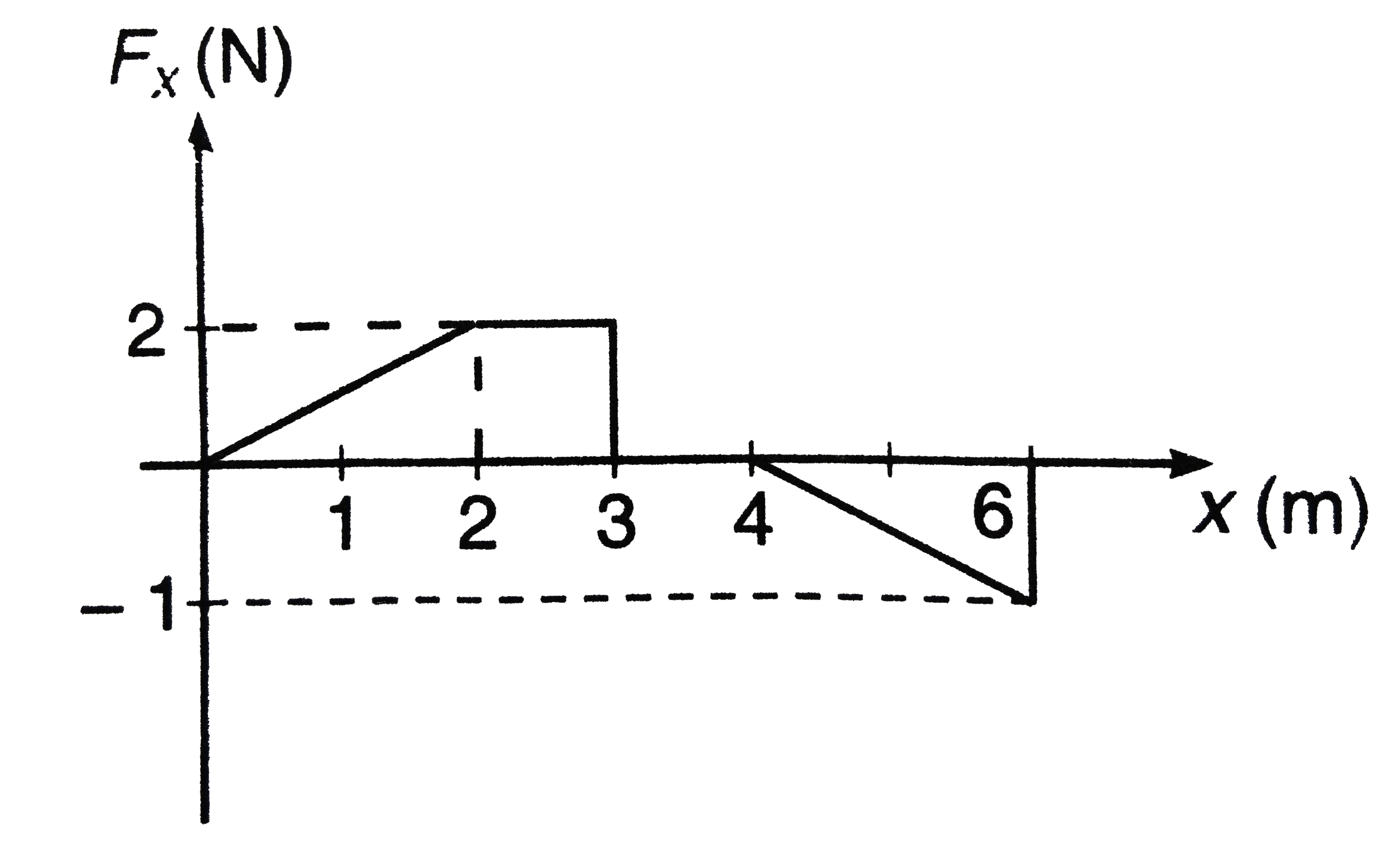
View SolutionA child applies a force F parallel to the x-axis to block moving on a horizontal surface. As the child controls the speed of the block, the x-component of the force varies with the x-coordinate of the block as shown in figure. calculate the work by the force F whin the block moves.
 .
.
(a) from x=0 to x=3.0m
(b) from x=3.0m to x=4.0m
(c) from x=4.0m to x=7.0m
(d) from x=0 to x=7.0m.
View SolutionIn Fig 15.5, the block has a kinetic energy of 3J and the spring has an elastic potential energy of 2J when the block is at x=+2.0cm. (a) What is the kinetic energy when the block is at x= 0? What is the elastic potential energy when the block is at (b) x=−2.0cm and (c ) x=−xm?
View SolutionA block of mass 4 kg hangs from a spring constant k=400Nm. The block is pulled down through 15 cm below and released. What is its kinetic energy when the block is 10 above the equilibrium position.?
View SolutionIn previous question, if we pull the block by the force F making an angle theta and the block remains stationary, the value of friction force is.

View Solution