A spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
v√(mk)
mv√k
m√(vk)
k√(mv)
The correct Answer is:A
Step by step video, text & image solution for A spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICS, FORCESBOOK - D MUKHERJEECHAPTER - KINEMATICS, FORCESEXERCISE - Type 2
22 Videos
- IIT QUESTIONS 5BOOK - D MUKHERJEECHAPTER - IIT QUESTIONS 5EXERCISE - Matrix matching type
2 Videos
- MISCELLANEOUS QUESTION 1BOOK - D MUKHERJEECHAPTER - MISCELLANEOUS QUESTION 1EXERCISE - Miscellaneous Questions-1 (Straight-Objective Type)
54 Videos
Similar Questions
A block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionA block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View Solution
Knowledge Check
A block of mass m, attacted to a string of spring constant k, oscillates on a smooth horizontal table. The other end of the spring is fixed to a wall. The block has a speed v when the spring is at its natural length. Before coming to an instantaneous rest. If the block moves a distance x from the mean position, then
Ax=√mkBa=1v√mkCx=v√mkDx=√mvkA block A of mass M is placed in contact with a fixed spring of length l and force constant k and free from a smooth wall at a distance l on the other side. If the block is given a velocity v as shown, the time taken by the block to strike on the wall will be
 Aπ√Mk+lvBπ√MkC2π√Mk+2lvDπ√Mk+2lv
Aπ√Mk+lvBπ√MkC2π√Mk+2lvDπ√Mk+2lvA particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
 Amω2lkBmω2lk−mω2Cmω2lk+mω2Dnone of these
Amω2lkBmω2lk−mω2Cmω2lk+mω2Dnone of these
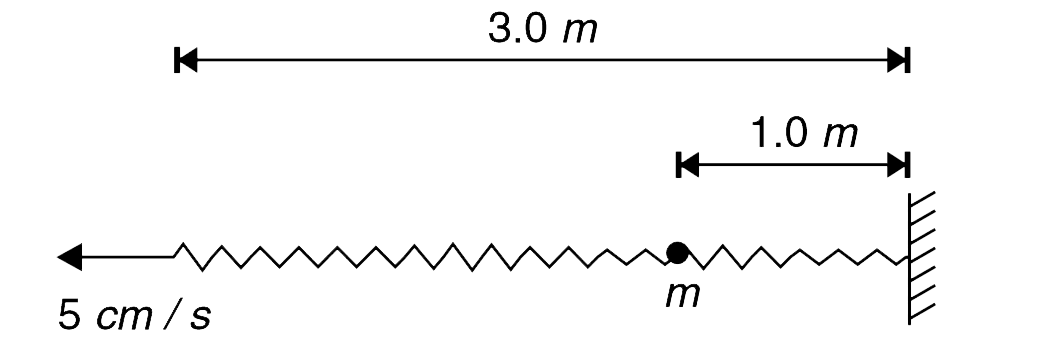
A uniform light spring has unstretched length of 3.0 m. One of its end is fixed to a wall. A particle of mass m = 20 g is glued to the spring at a point 1.0 m away from its fixed end. The free end of the spring is pulled away from the wall at a constant speed of 5 cm/s. Assume that the spring remains horizontal (i.e., neglect gravity). Force constant of spring = 0.6 N / cm.
(a) With what speed does the particle of mass m move?
(b) Find the force applied by the external agent pulling the spring at time 2.0 s after he started pulling.
View SolutionAn ideal spring with spring - constant K is bung from the colling and a block of mass M is attached to its lower end the mass is released with the spring initally unstetched . Then the maximum exlemsion in the spring is
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View SolutionA block attached with an ideal spring is kept on a smooth horizontal surface. Now the free end of the spring is pulled with a constant velocity u horizontally. Then the maximum energy stored in the spring and bock system during subsequent motion is :
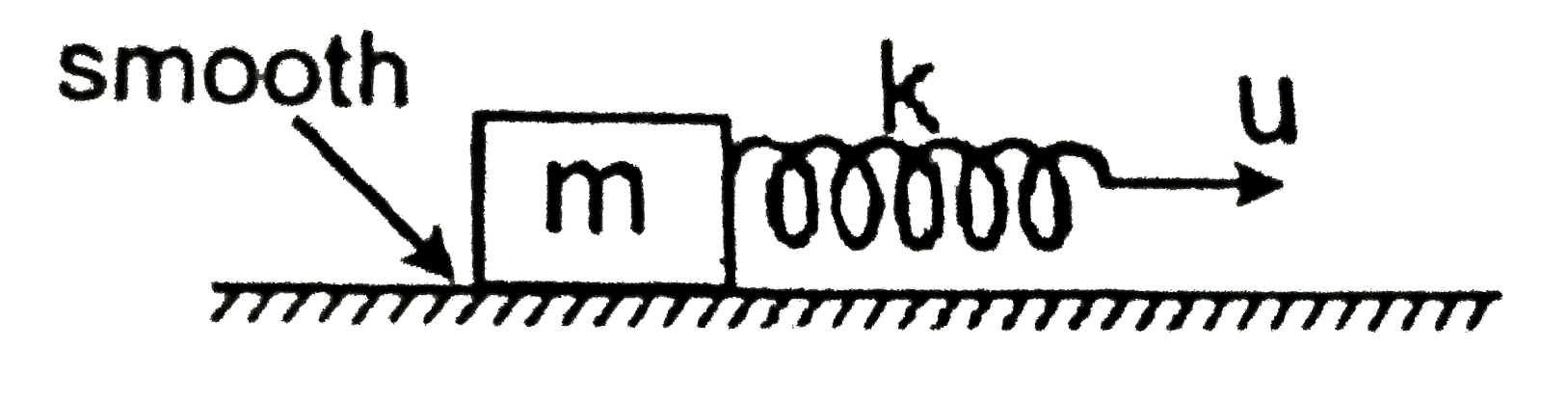
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View Solution
