A spring of natural length l is compressed vertically downward against the floor so that its compressed lengtg becomes 12. On releasing, the spring attins its natural length. If k is the siffness constant of spring, then the work done by the spring on the floor is
zero
12kl2
12k(l22)
kl2
The correct Answer is:A
To solve the problem, we need to determine the work done by the spring on the floor when it is compressed and then released.
1. Understanding the Spring Compression:
- The spring has a natural length l. When compressed, its length becomes l2. This means the spring is compressed by a distance of:
\(
\Delta x = l - \frac{l}{2} = \frac{l}{2}
\)
2. Calculating the Force Exerted by the Spring:
- The force exerted by the spring when it is compressed can be calculated using Hooke's Law:
\(
F = k \Delta x
\)
- Substituting the value of \(\Delta x\):
\(
F = k \cdot \frac{l}{2}
\)
3. Understanding Work Done:
- The work done by the spring when it returns to its natural length can be calculated using the formula for work done by a variable force:
\(
W = \frac{1}{2} k (\Delta x)^2
\)
- Substituting \(\Delta x = \frac{l}{2}\):
\(
W = \frac{1}{2} k \left(\frac{l}{2}\right)^2 = \frac{1}{2} k \cdot \frac{l^2}{4} = \frac{kl^2}{8}
\)
4. Considering the Work Done on the Floor:
- However, the question specifically asks for the work done by the spring on the floor. Since the floor does not move (it is fixed), the displacement \(s\) of the floor is 0.
- Therefore, the work done by the spring on the floor is:
\(
W_{\text{floor}} = F \cdot s = F \cdot 0 = 0
\)
5. Conclusion:
- The work done by the spring on the floor is zero because there is no displacement of the floor.
Final Answer:
The work done by the spring on the floor is 0.
- The spring has a natural length l. When compressed, its length becomes l2. This means the spring is compressed by a distance of:
\(
\Delta x = l - \frac{l}{2} = \frac{l}{2}
\)
- The force exerted by the spring when it is compressed can be calculated using Hooke's Law:
\(
F = k \Delta x
\)
- Substituting the value of \(\Delta x\):
\(
F = k \cdot \frac{l}{2}
\)
- The work done by the spring when it returns to its natural length can be calculated using the formula for work done by a variable force:
\(
W = \frac{1}{2} k (\Delta x)^2
\)
- Substituting \(\Delta x = \frac{l}{2}\):
\(
W = \frac{1}{2} k \left(\frac{l}{2}\right)^2 = \frac{1}{2} k \cdot \frac{l^2}{4} = \frac{kl^2}{8}
\)
- However, the question specifically asks for the work done by the spring on the floor. Since the floor does not move (it is fixed), the displacement \(s\) of the floor is 0.
- Therefore, the work done by the spring on the floor is:
\(
W_{\text{floor}} = F \cdot s = F \cdot 0 = 0
\)
- The work done by the spring on the floor is zero because there is no displacement of the floor.
The work done by the spring on the floor is 0.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion And Reason
12 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

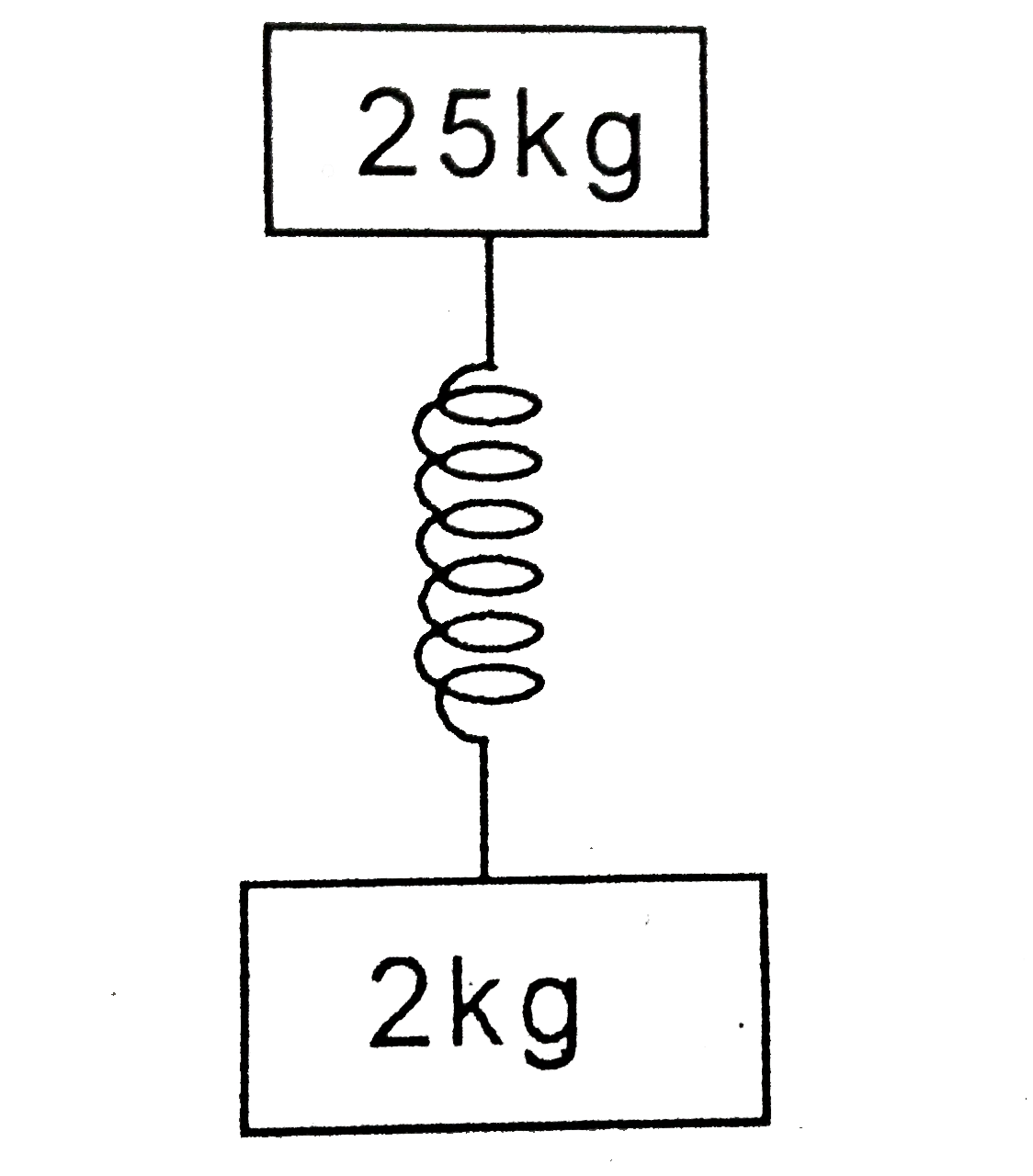
View SolutionInitialy spring in its natural length now a block at mass 0.25 kg is released then find out maximum force by system on floor ?
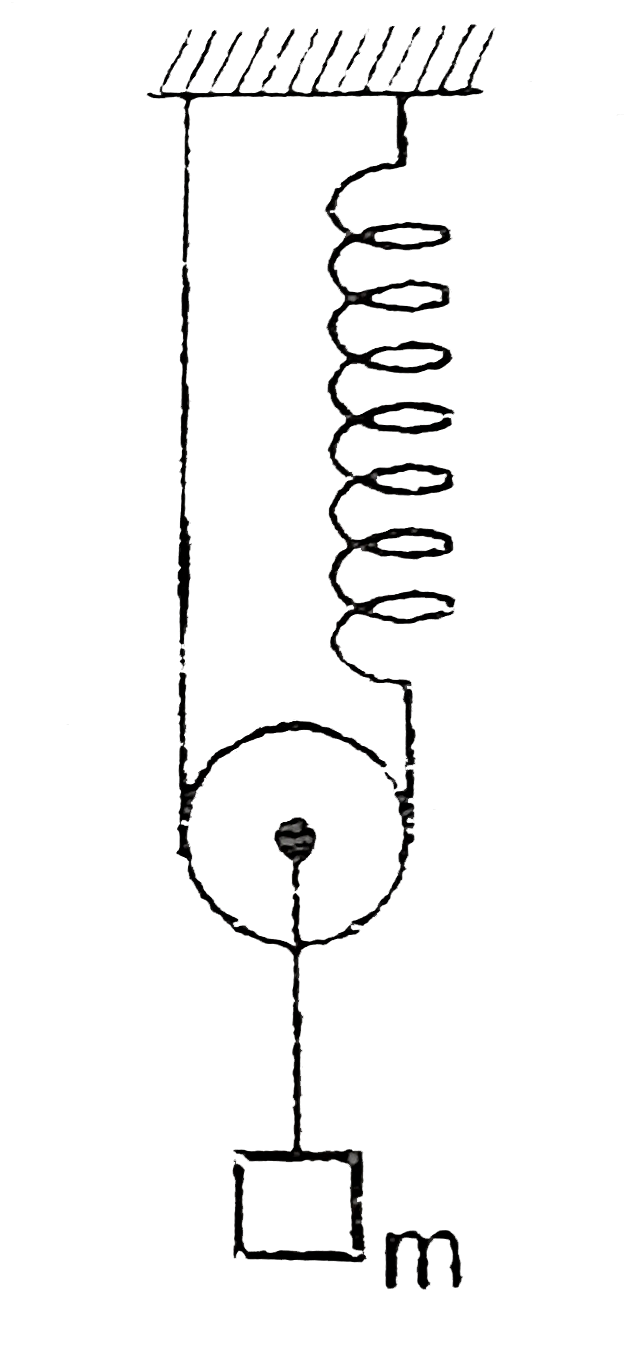
View SolutionThe system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionA system of wedge and block as shown in figure, is released with the spring in its natural length. All surfaces are frictionless. Maximum elongation in the spring will be
 .
.
View SolutionIn the previous illustration. Consider the situation when the string is completely compressed. Then it begins to relax and will come to its original length.
a. What is the work done by the spring during the period?
b. Is the work done by the spring positive or negative?
View SolutionA spring is stretched by distance x and then compressed to same distance from its original length. The work done by the spring force is (k=spring constant)
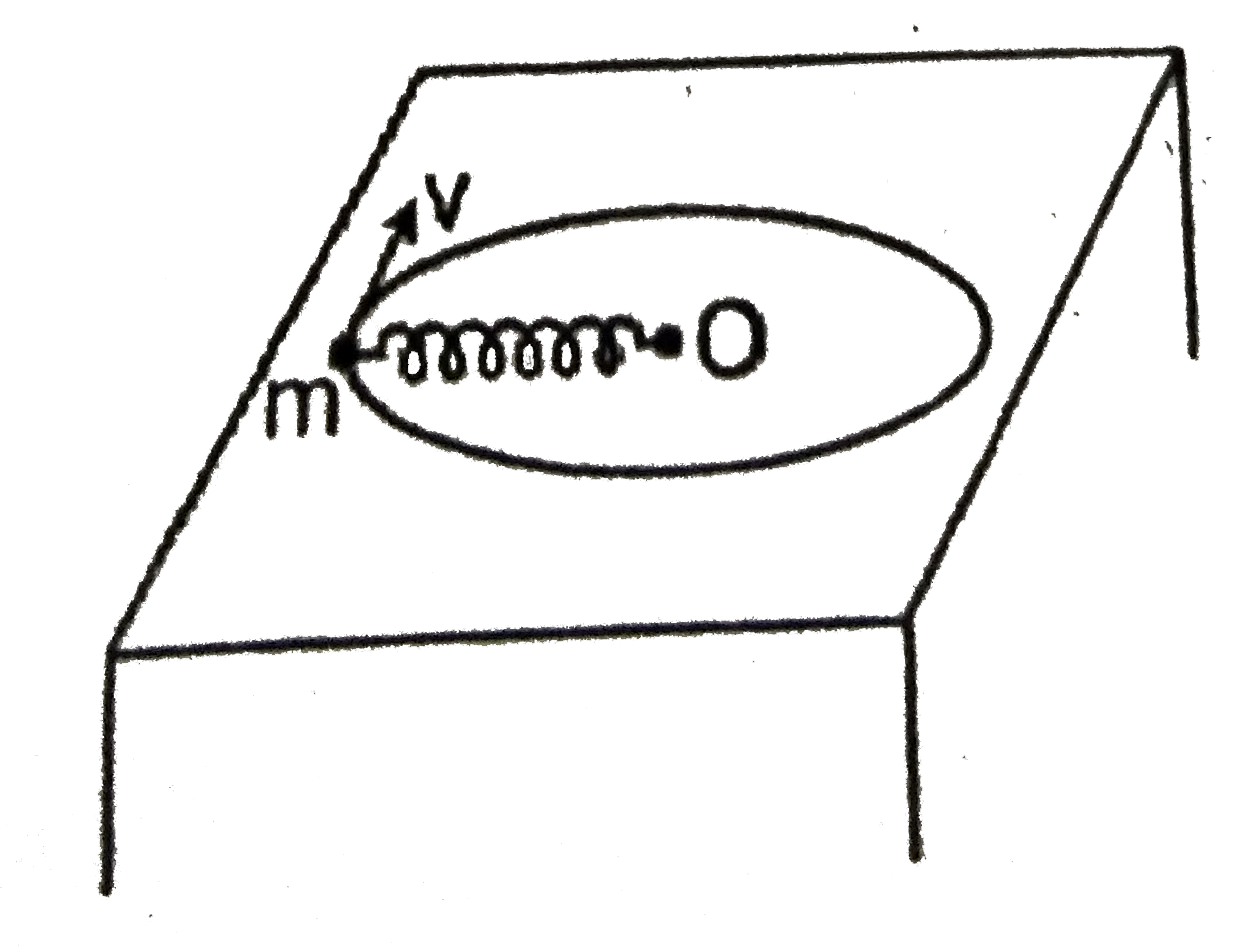
View SolutionMass m is connected with an ideal spring of natural length l whose other end is fixed on a smooth horizontal table. Initially spring is in its natural length l. Mass m is given a velocity 'v' perpendicular to the spring and released . The velocity perpendicular to the spring when its length l+x , will be
View SolutionA dumbbell consists of two balls A and B of mass m=1 kg and connected by a spring. The whole system is placed on a smooth horizontal surface as shown in the figure. Initially the spring is at its natural length, the ball B is imparted a velocity v0=8√7m/s in the direction shown. The spring constant of the spring is adjusted so that the length of the spring at maximum elongation is twice that of the natural, length of the spring. Find the maximum potential energy stored (in Joule) in the spring during the motion.

View SolutionA plank of mass 5kg is placed on a frictionless horizontal plane. Further a block of mass 1kg is placed over the plank. A massless spring of natural length 2m is fixed to the plank by its one end. The other end of spring is compressed by the block by half of spring's natural length. They system is now released from the rest. What is the velocity of the plank when block leaves the plank? (The stiffness constant of spring is 100N/m)

View Solution
