A spring stores 5J of energy when stretched by 25 cm. It is kept vertical with the lower end fixed. A block fastened to its end is made to undergo small oscillations. If the block makes 5 oscillations each second what is the mass of the block?
0.16kg
1.6kg
16kg
0.016kg
The correct Answer is:C
To solve the problem step by step, we will follow the given information and apply relevant formulas.
Step 1: Understand the Energy Stored in the Spring
The potential energy (PE) stored in a spring when it is stretched is given by the formula:
PE=12kx2
where k is the spring constant and x is the displacement from the equilibrium position.
Step 2: Convert Units
We are given that the spring is stretched by 25 cm. We need to convert this to meters:
x=25 cm=0.25 m
Step 3: Set Up the Equation for Potential Energy
We know the potential energy stored in the spring is 5 J. Substituting the values into the potential energy formula:
5=12k(0.25)2
Step 4: Solve for the Spring Constant k
Now, we can solve for k:
5=12k(0.0625)(since 0.252=0.0625)
5=12k⋅0.0625
10=k⋅0.0625
k=100.0625=160 N/m
Step 5: Determine the Frequency of Oscillation
The problem states that the block makes 5 oscillations each second. Thus, the frequency f is:
f=5 Hz
Step 6: Calculate the Time Period T
The time period T is the reciprocal of the frequency:
T=1f=15=0.2 seconds
Step 7: Use the Time Period Formula for a Spring-Mass System
The time period T for a mass-spring system is given by:
T=2π√mk
Substituting the known values:
0.2=2π√m160
Step 8: Solve for Mass m
First, isolate the square root:
0.22π=√m160
Now square both sides:
(0.22π)2=m160
Calculating the left side:
0.044π2=m160
Now multiply both sides by 160:
m=160⋅0.044π2
m=160⋅0.044π2=6.4π2
Using π2≈10:
m≈6.410=0.64 kg
Final Answer
The mass of the block is approximately:
m≈0.16 kg or 160 grams
The potential energy (PE) stored in a spring when it is stretched is given by the formula:
PE=12kx2
where k is the spring constant and x is the displacement from the equilibrium position.
We are given that the spring is stretched by 25 cm. We need to convert this to meters:
x=25 cm=0.25 m
We know the potential energy stored in the spring is 5 J. Substituting the values into the potential energy formula:
5=12k(0.25)2
Now, we can solve for k:
5=12k(0.0625)(since 0.252=0.0625)
5=12k⋅0.0625
10=k⋅0.0625
k=100.0625=160 N/m
The problem states that the block makes 5 oscillations each second. Thus, the frequency f is:
f=5 Hz
The time period T is the reciprocal of the frequency:
T=1f=15=0.2 seconds
The time period T for a mass-spring system is given by:
T=2π√mk
Substituting the known values:
0.2=2π√m160
First, isolate the square root:
0.22π=√m160
Now square both sides:
(0.22π)2=m160
Calculating the left side:
0.044π2=m160
Now multiply both sides by 160:
m=160⋅0.044π2
m=160⋅0.044π2=6.4π2
Using π2≈10:
m≈6.410=0.64 kg
The mass of the block is approximately:
m≈0.16 kg or 160 grams
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective-2
15 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Objective-2
7 Videos
Similar Questions
A vertical spring-mass system with lower end of spring is fixed, made to undergo small oscillations. If the spring is stretched by 25cm, energy stored in the spring is 5J. Find the mass of the block if it makes 5 oscillations each second.
View SolutionFind the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.

View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA spring of force constant 200Nm−1 has a block of mass 10 kg hanging at its one end and the other end of the spring is attached to the celling of an elevator. The elevator is rising upwards with an acceleration of g4 and the block is in equilibrium with respect to the elevator . when the acceleration of the elevator suddenly ceases , the block starts oscillating . What is the amplitude (in m) of these oscillations ?
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA wire of length l, area of cross-section A and Young,s modulus of elasticity Y is suspended form the roof of a building. A block of mass m is attached at lower end of the wire. If the block is displaced from its mean position and released then the block starts oscillating. Time period of these oscillations will be

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View Solution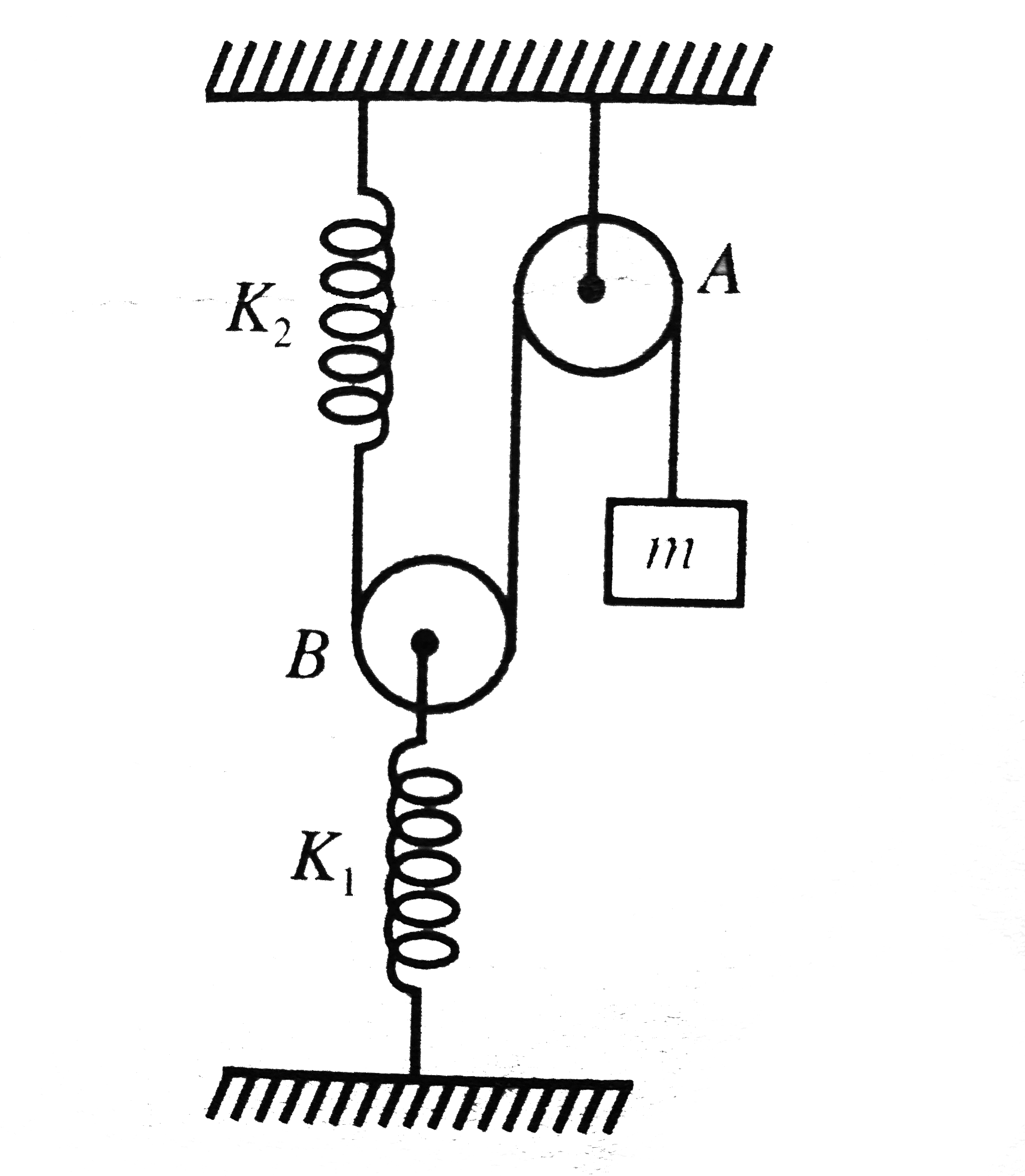
A block of mass m is tied to one end of a spring which passes over a smooth fixed pulley A and under a light smooth movable pulley B. The other end of the string is attached to the lower end of a spring of spring constant K2. Find the period of small oscillation of mass m about its equilibrium position (in second). (Take m=π2kg,K2k=4K1,K1=17Nm.)
View Solution
