Question

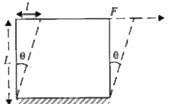
A square aluminium of side 50cm and thickness 5cm is subjected to a shearing force of magnitude ${10}^{4}N$. The lower edge is revetted to the floor. How much is the upper edge displaced if shear modulus of aluminium is $2.5\times {10}^{10}N{m}^{-2}$ ?

Answer

`8 xx 10^(-6) m`

Explanation

To solve the problem step by step, we will follow the outlined procedure to find the displacement of the upper edge of the aluminum slab when subjected to a shearing force.

Step 1: Identify the given values
- Side of the square aluminum slab (L) = 50 cm = 0.5 m
- Thickness of the slab (t) = 5 cm = 0.05 m
- Shearing force (F) = \(10^4\) N
- Shear modulus of aluminum (G) = \(2.5 \times 10^{10}\) N/m²

Step 2: Calculate the area subjected to shearing stress
The area (A) on which the shearing force acts can be calculated using the formula:
\( A = L \times t \)
Substituting the values:
\( A = 0.5 \, \text{m} \times 0.05 \, \text{m} = 0.025 \, \text{m}^2 \)

Step 3: Calculate the shearing stress
Shearing stress (\( \tau \)) is given by:
\( \tau = \frac{F}{A} \)
Substituting the values:
\( \tau = \frac{10^4 \, \text{N}}{0.025 \, \text{m}^2} = 4 \times 10^6 \, \text{N/m}^2 \)

Step 4: Relate shear modulus, shear stress, and shear strain
The shear modulus (G) is defined as:
\( G = \frac{\tau}{\text{shear strain}} \)
Where shear strain is given by:
\( \text{shear strain} = \frac{\Delta L}{L} \)
Thus, we can write:
\( G = \frac{\tau}{\frac{\Delta L}{L}} \)
Rearranging gives:
\( \Delta L = \frac{\tau \cdot L}{G} \)

Step 5: Substitute the values to find the displacement (\( \Delta L \))
Now substituting the values we have:
\( \Delta L = \frac{(4 \times 10^6 \, \text{N/m}^2) \cdot (0.5 \, \text{m})}{2.5 \times 10^{10} \, \text{N/m}^2} \)
Calculating this gives:
\( \Delta L = \frac{2 \times 10^6}{2.5 \times 10^{10}} = 8 \times 10^{-6} \, \text{m} \)

Final Answer
The upper edge of the aluminum slab is displaced by \( \Delta L = 8 \times 10^{-6} \, \text{m} \) or \( 8 \, \mu m \).

---