A metallic cube whose each side is 10 cm is subjected to a shearing force of 100 kgf. Calculate the shearing produced.
9.8×104Nm−2
10Nm−2
9.8Nm−2
9.8×102Nm−2
The correct Answer is:A
To solve the problem of calculating the shearing produced in a metallic cube subjected to a shearing force, we will follow these steps:
Step 1: Understand the Given Data
- The side length of the metallic cube (L) = 10 cm = 0.1 m (conversion from cm to m)
- The shearing force (F) = 100 kgf
Step 2: Convert the Shearing Force to Newtons
1 kgf (kilogram-force) is equivalent to 9.8 N (newtons). Therefore, we convert the shearing force:
F=100kgf×9.8N/kgf=980N
Step 3: Calculate the Area of One Face of the Cube
The area (A) of one face of the cube can be calculated using the formula:
A=L2
Substituting the value of L:
A=(0.1m)2=0.01m2
Step 4: Calculate the Shearing Stress
Shearing stress (τ) is defined as the force (F) applied per unit area (A):
τ=FA
Substituting the values:
τ=980N0.01m2=98000N/m2=98kPa
Step 5: Calculate the Shearing Produced
To find the shearing produced (which is often represented as the shear strain), we can use the relationship between shear stress and shear modulus (G):
Shearing produced=τG
However, since we do not have the value of the shear modulus (G) for the metallic cube, we will stop at the shearing stress calculation.
Final Result
The shearing stress produced in the metallic cube is:
τ=98000N/m2 or 98kPa
- The side length of the metallic cube (L) = 10 cm = 0.1 m (conversion from cm to m)
- The shearing force (F) = 100 kgf
1 kgf (kilogram-force) is equivalent to 9.8 N (newtons). Therefore, we convert the shearing force:
F=100kgf×9.8N/kgf=980N
The area (A) of one face of the cube can be calculated using the formula:
A=L2
Substituting the value of L:
A=(0.1m)2=0.01m2
Shearing stress (τ) is defined as the force (F) applied per unit area (A):
τ=FA
Substituting the values:
τ=980N0.01m2=98000N/m2=98kPa
To find the shearing produced (which is often represented as the shear strain), we can use the relationship between shear stress and shear modulus (G):
Shearing produced=τG
However, since we do not have the value of the shear modulus (G) for the metallic cube, we will stop at the shearing stress calculation.
The shearing stress produced in the metallic cube is:
τ=98000N/m2 or 98kPa
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.215videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Check point 12.315videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELASTICITYEXERCISE - Level 2 Subjective10videos
ELASTICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions469videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
Similar Questions
A metalic cube whose side is 10cm is subjected to a shearing force of 100 N. The top face is displaced through 0.25cm with respect to the bottom . Calculate the shearing stress, strain and shear modulus.
View SolutionA metallic cube of side 10 cm is subjected to a shearing force of 300 kgf. The top force is displaced through 0.25 cm with respect ot the bottom ? Calculate the shearing strain produced .
View Solution
Knowledge Check
- Question 1 - Select One
The metal cube of side 10 cm is subjected to a shearing stress of 104Nm−2. The modulus of rigidity if the top of the cube is displaced by 0.05 cm with respect to its bottom is
A2×106Nm−2B10x5Nm−2C1×107Nm−2D4×105Nm−2
A metal cube of side 10cm is subjected to a shearing stress of 106N/m2. Calculate the modulus of rigidity if the of the cube is displaced by 0.05cm with respect to its bottom.
View SolutionA metal cube of side 20cm is subjected to a shearing force of 4000N. The top face is displaced through 0.50 cm with respect to the bottom. Find the rigidity modulus of the metal.
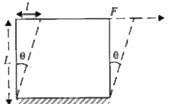 View Solution
View SolutionA lead cube of side 20 cm is subjected under a shearing force of magnitude 5.6x106N. If the lower face of the cube is fixed, then the displacement in the upper face is (If shear modulus of lead is 5.6⋅106Nm2)
View SolutionA square aluminium of side 50cm and thickness 5cm is subjected to a shearing force of magnitude 104N. The lower edge is revetted to the floor. How much is the upper edge displaced if shear modulus of aluminium is 2.5×1010Nm−2 ?
View SolutionA 0.05m cube has its upper face displaced by 0.2cm by a tangential force of 8N. Calculate the shearing strain, shearing stress and modulus of rigidity of the material of the cube.
View SolutionA 4 cm cube has its upper face displaced by 0.1 mm by a tangential force of 8 kN. Calculate the shear modulus of the cube.
View SolutionA square lead slab of side 50 cm and thickness 10 cm is subjected to a shearing force (on its narrow face) of 9×104N. The lower edge is riveted to the floor. How much will the upper edge be displaced? (Shear modulus of lead=5.6×109Nm−2)
View Solution

