A square frame of side 1 m carries a current I, produces a magnetic field B at its centre. The same current is passed through a circular coil having the same perimeter as the square. The magnetic field at the centre of the circular coil is B'. The ratio $B / B$ is

A

$\frac{8}{π^{2}}$

B

$\frac{8 \sqrt{2}}{π^{2}}$

C

$\frac{16}{π^{2}}$

D

$\frac{16 \sqrt{2}}{π^{2}}$

Text Solution

Verified by Experts

The correct Answer is:B

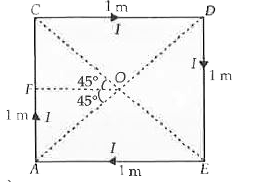Refer figure,
$tan = \frac{C F}{O F}, O F = C F = \frac{1}{2} M$
The agnetic field at the centre O of the square frame is
$B = \frac{μ_{0}}{4 π} \frac{1}{(1 / 2)} [{sin 45}^{\circ} + {sin 45}^{\circ}] \times 4 \frac{μ_{0}}{4 π} (17 I) (\sqrt{2})$
When the frame is taken as curcular coil of radius r, then
$2 π r = 4 or r = \frac{2}{π}$
The magnetic field at the centre of the circular coil carrying same current I a is
$B^{.} = \frac{μ_{0}}{4 π} \frac{2 π I}{r} = \frac{μ_{0}}{4 π} \frac{2 π I}{2 / π} = \frac{μ_{0}}{4 π} π^{2} I$
$∴ \frac{B}{B^{.}} = \frac{16}{\sqrt{2} π^{2}} = \frac{8 \sqrt{2}}{π^{2}}$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A square frame of side $l$ carries a current produces a field $B$ at its centre. The same current is passed through a circular loop having same perimeter as the square. The field at its centre is $B'$ , the ratio of $B / B'$ is
A $\frac{8}{π^{2}}$
B $\frac{8 \sqrt{2}}{π^{2}}$
C $\frac{16}{π^{2}}$
D $\frac{16 \sqrt{2}}{π^{2}}$
Question 2 - Select One
A square frame of side $l$ carries a current produces a field $B$ at its centre. The same current is passed through a circular loop having same perimeter as the square. The field at its centre is $B'$ , the ratio of $B / B'$ is
A $\frac{8 \sqrt{2}}{π^{2}}$
B $\frac{8}{π^{2}}$
C $\frac{\sqrt{2}}{π^{2}}$
D $\frac{π^{2}}{8 \sqrt{2}}$
Question 3 - Select One
A circular coil carrying a certain, current produces a magnetic field $B_{0}$ at its centre. The coil is now rewound so a to have 3 turns and the same currents is passed through it. The new magnetic field at the centre is
A $\frac{B_{0}}{9}$
B $9 B_{0}$
C $\frac{B_{0}}{3}$
D $3 B_{0}$

MTG GUIDE-MAGNETIC EFFECTS OF CURRENT AND MAGNETISM-NEET CAFE (TOPICWISE PRACTICE QUESTIONS)(BIOT SAVART LAW AND ITS APPLICATIONS)

Home
Ask Doubt
Profile