A square of side a and uniform thickness is divided into four equal parts. If upper right part is removed, then find the coordinates of centre of mass of remaining part.
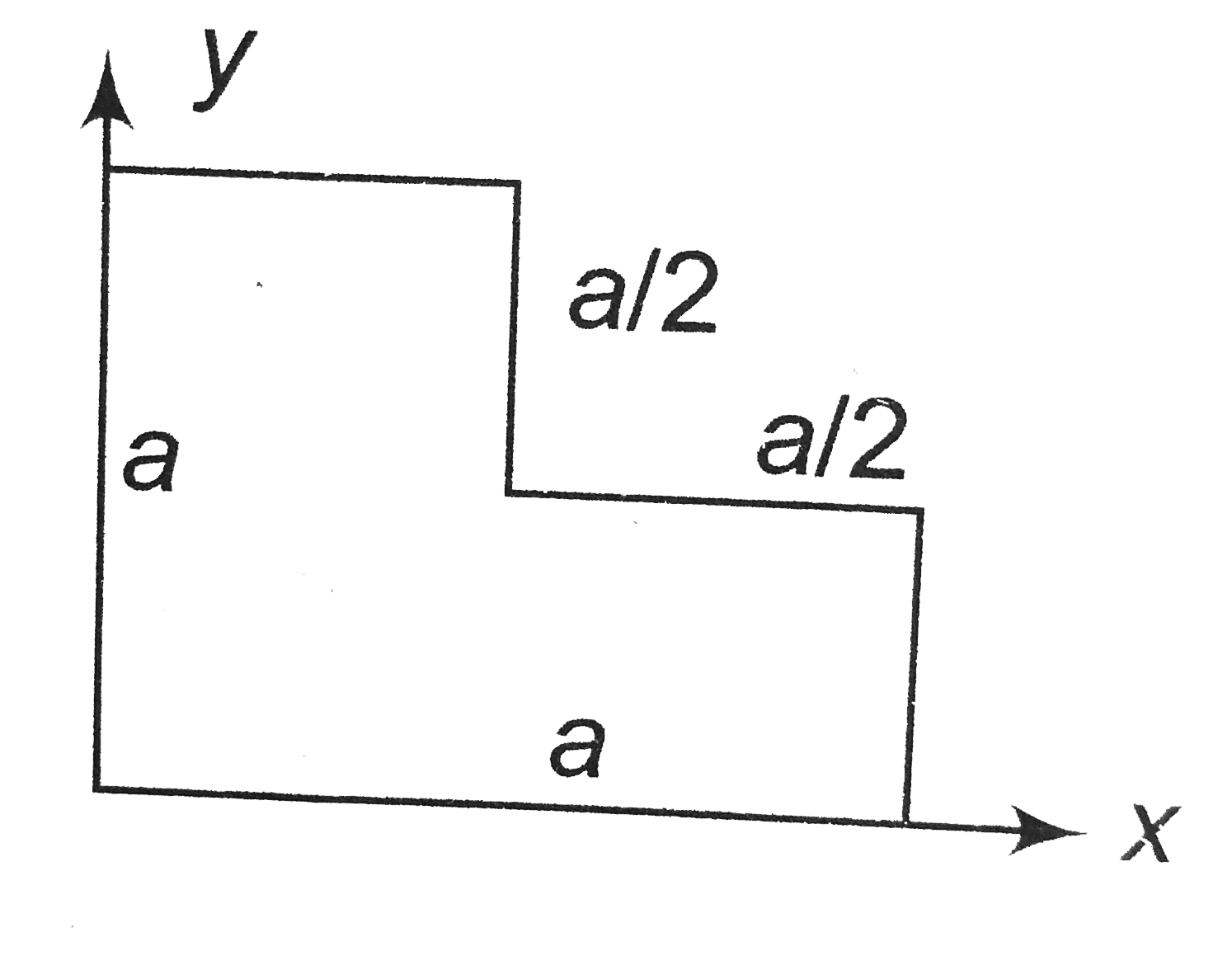 .
.
(512a,512a)
(712a,712a)
(14a,14a)
(13a,13a)
The correct Answer is:A
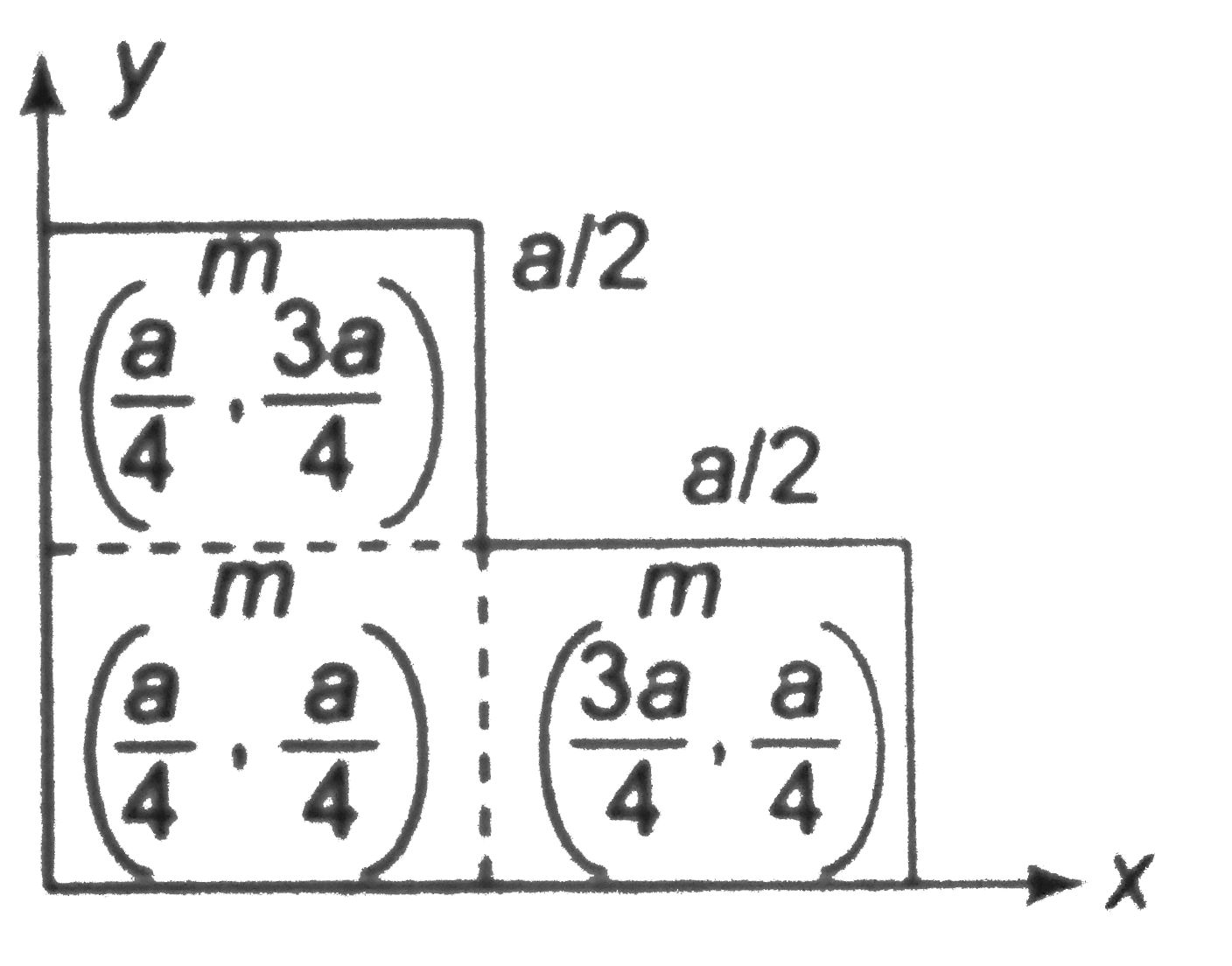
(a) Let mass of each is m. Coordinates of their respective centre of masses are shown in figure.
xcm=ma4+m3a4+ma4m+m+m=5a12
xcm=ma4+ma4+m3a4m+m+m=5a12.
 .
.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Displacement , Velocity And Acceleration Of Centre Of Mass30videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Moment Of Inertia39videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test30videos
THERMAL PROPERTIES OF MATTER
Similar Questions
A square of side 4 cm and of uniform thickness is divided into four equal squares. If one of them is cut off (OECF), then the position of the centre of mass of the remaining portion from O is √2kcm . Find the value of K.
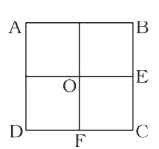 View Solution
View SolutionA square of side 4m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find

the position of centre of mass of the remaining portion from the centre O.View Solution
Knowledge Check
- Question 1 - Select One
A square of side 2cm and uniform thickness is divided into four squares. The square portion A′AB′D is removed and the removed portion is placed over the portion DB′BC′. The new position of centre of mass is
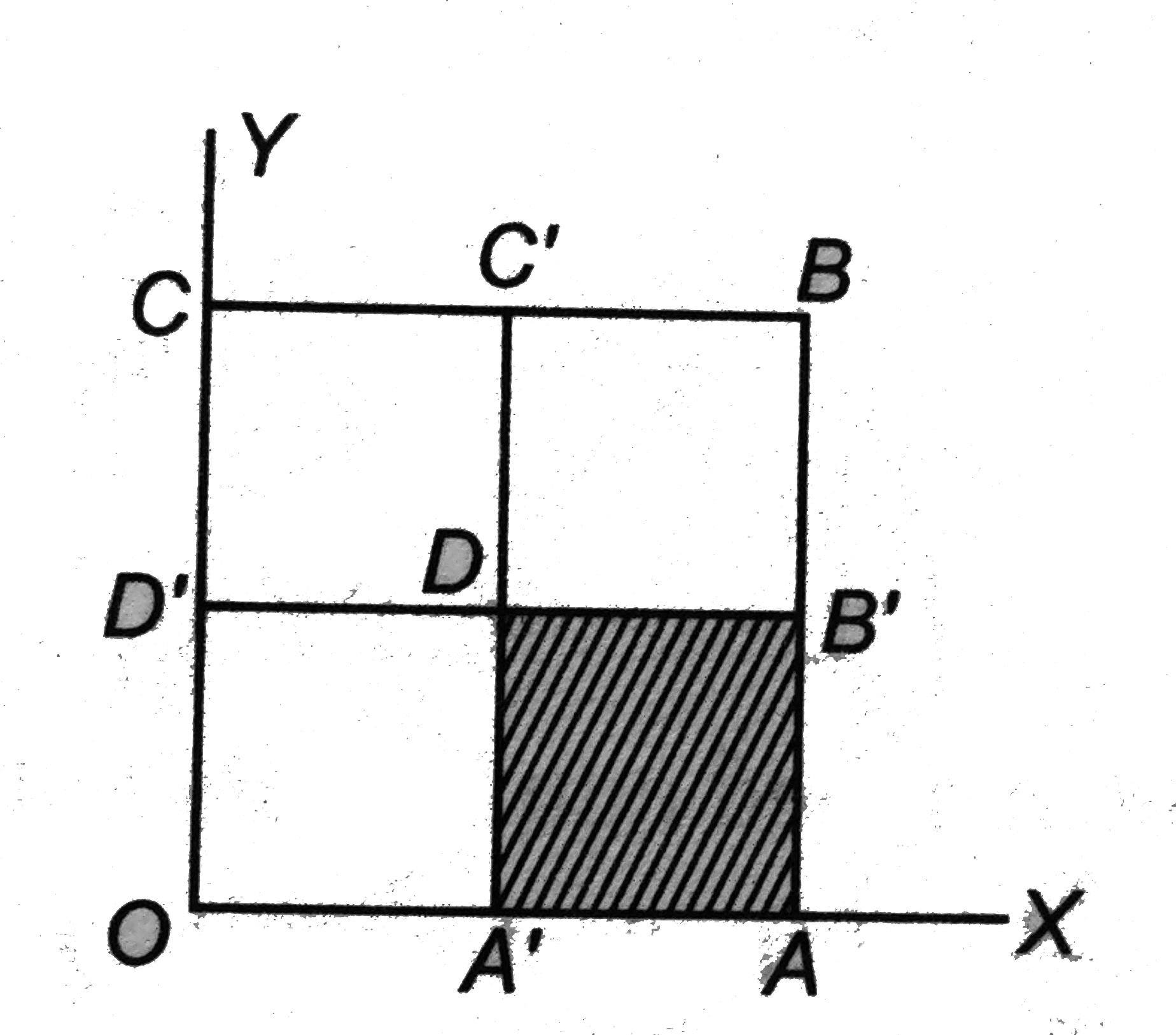 A(2cm,2cm)B(2cm,3cm)C(2cm,2.5cm)D(3cm,3cm)
A(2cm,2cm)B(2cm,3cm)C(2cm,2.5cm)D(3cm,3cm) - Question 2 - Select One
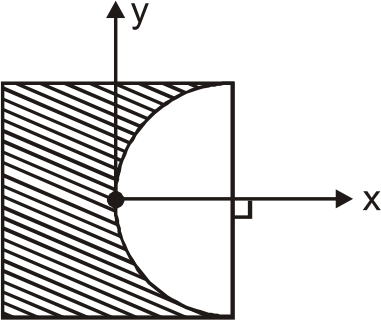
Figure shows a square plate of uniform thickness and side length √2m. One fourth of the plate is removed as indicated. The distance of centre of mass of the remaining portion from the centre of the original square plate is
 A1/3mB1/2mC1/6mD1/8m
A1/3mB1/2mC1/6mD1/8m - Question 3 - Select One
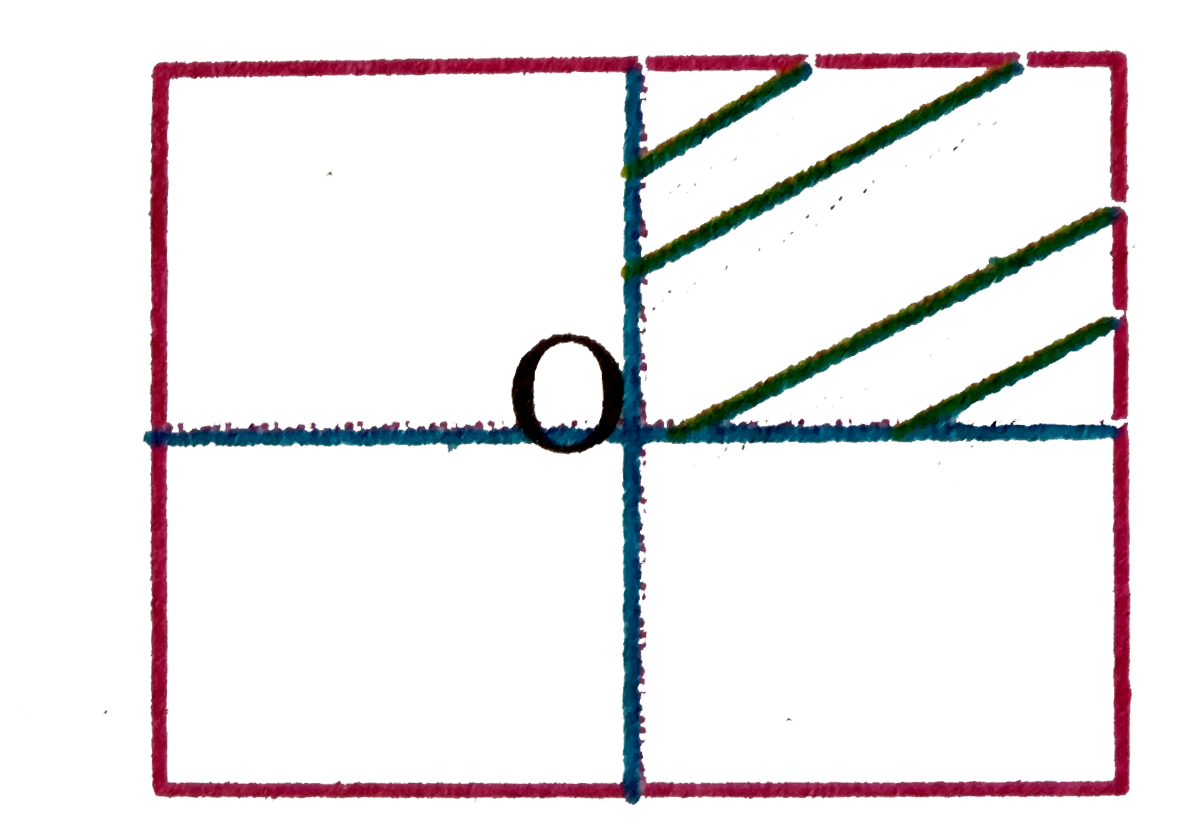
In the figure shown a semicircular area is removed from a uniform square plate of side l and mass ‘m’ (before removing). The x-coordinate of centre of mass of remaining portion is (The origin is at the centre of square)
 A−π(π−2)l2(8−π)Bπ(π−2)l2(8−π)C−π(π−2)l8−πD−l(π−43)2(8−π)
A−π(π−2)l2(8−π)Bπ(π−2)l2(8−π)C−π(π−2)l8−πD−l(π−43)2(8−π)
Fron a sqaure plate of side a,a quarter circular disc of radius a is removed as shown in figure. Find the coordinates of centre of mass of the remaining part.
 View Solution
View SolutionFrom a uniform square plate, one-fourth part is removed as shown. The centre of mass of remaining part will lie on
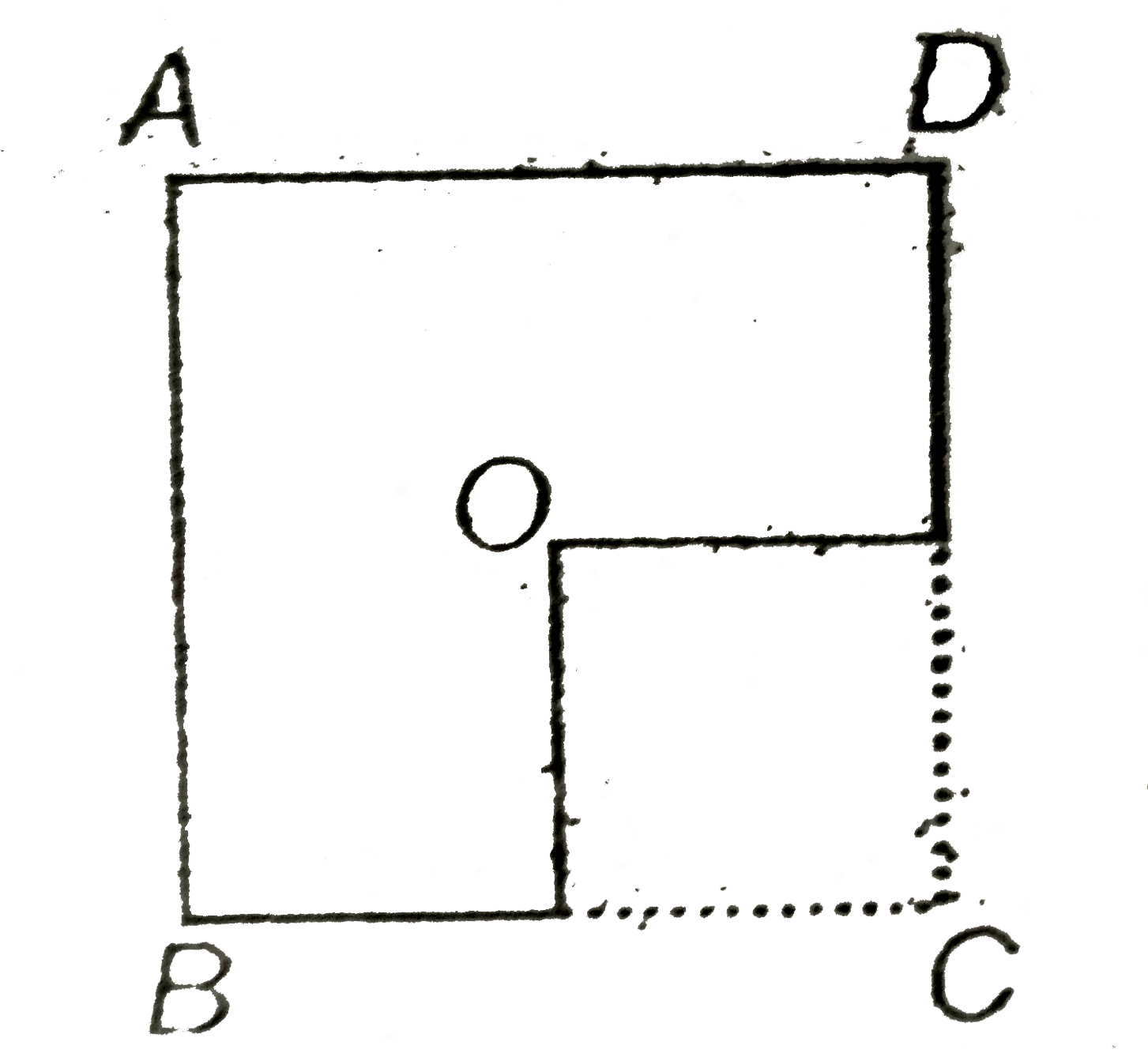 View Solution
View SolutionDegree: A right angle is divided into 90 equal parts. Each parts is called a degree.
View SolutionDraw an angle of measure 153∘ and divide it info four equal parts.
View SolutionA square plate of side 20cm has uniform thickness and density. A circular part of diameter 8cm is cut out symmetrically and shown in figure. The position of center of mass of the remaining potion is
 View Solution
View Solution

