A square plate of side 20cm has uniform thickness and density. A circular part of diameter 8cm is cut out symmetrically and shown in figure. The position of center of mass of the remaining potion is

at O1
at O
0.54 cm from O on the left hand side
None of the above
The correct Answer is:D
A1x1=A2x2 or x1=A2/A1.x−(2)=(π4)(8)2(20)2×6
= 0.7536 cm from O.
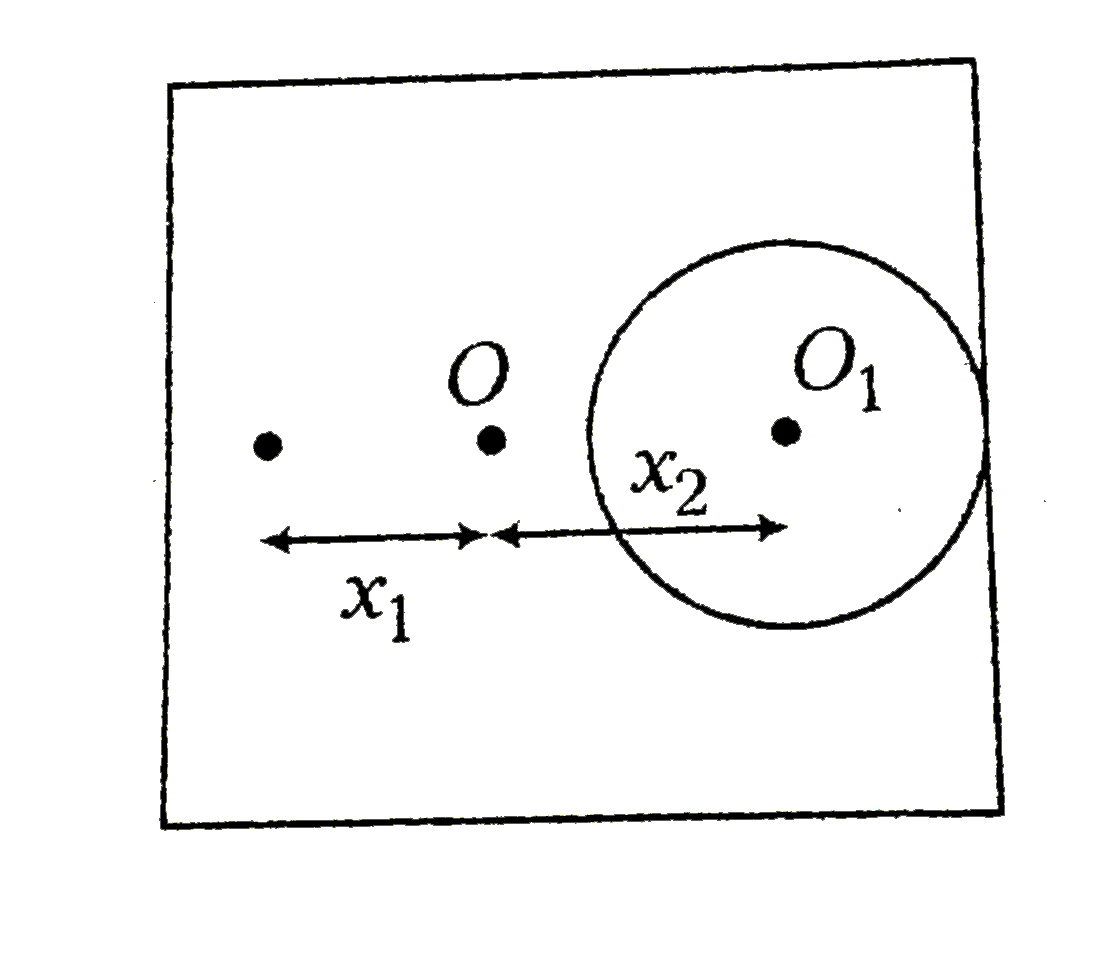
Topper's Solved these Questions
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Taking it together
73 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Assertion and reason
21 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
Similar Questions
A circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.
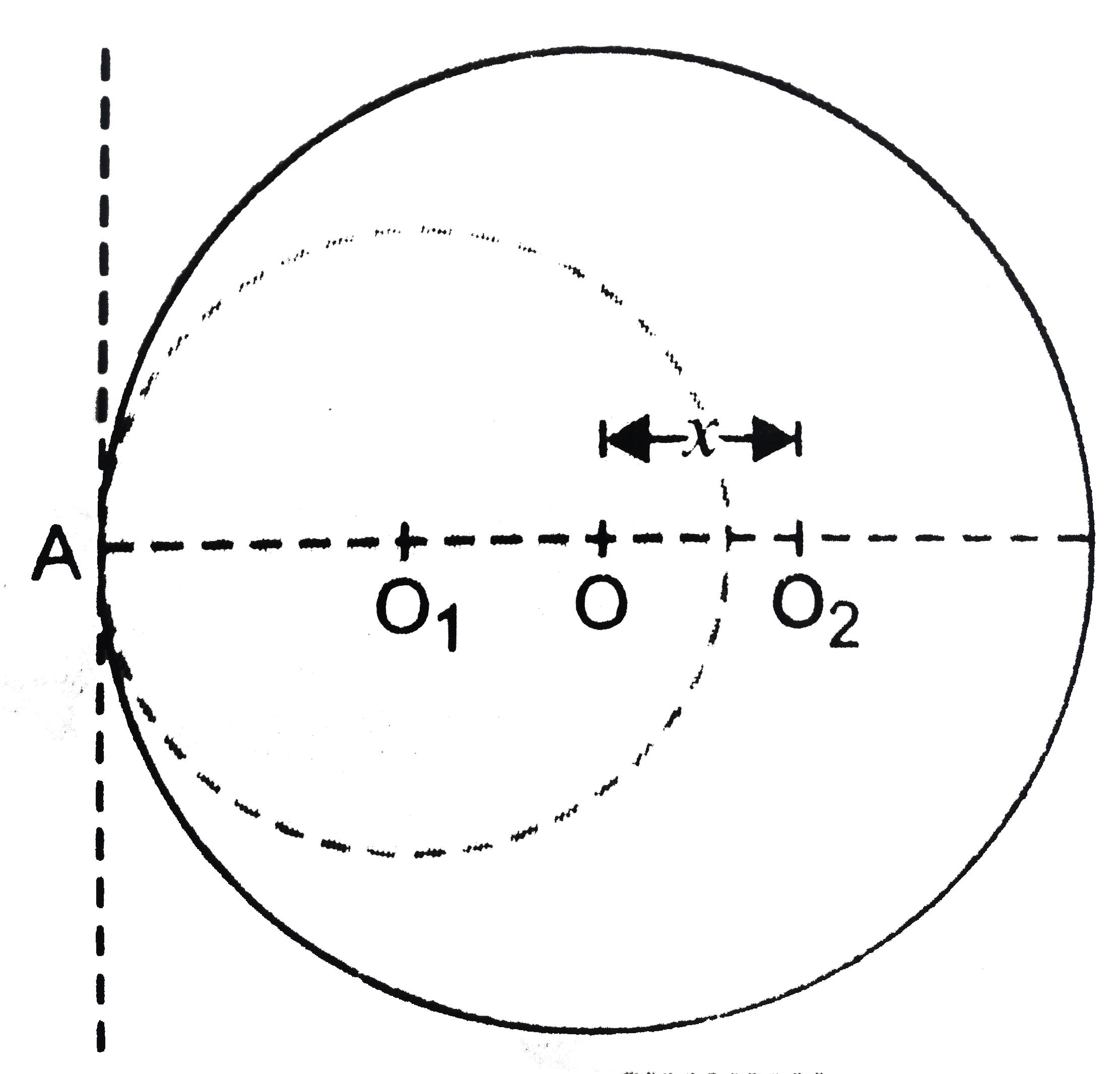
View SolutionA uniform circular plate of uniform thickness has a diameter of 56 cm. A circular portion of diameter 42 cm is removed from the edge of the plate. Find the position of the centre of mass of the remaining portion.
View Solution
Knowledge Check
A circular plate of uniform thickness has a diameter of 28cm. A circular portion of diameter 21cm is removed from the plate as shown. Ois the centre of mass of complete plate. The position of centre of mass of remaining portion will shift towards left from 'O' by
 A5cmB9cmC4.5cmD5.5cm
A5cmB9cmC4.5cmD5.5cmFigure shows a square plate of uniform thickness and side length √2m. One fourth of the plate is removed as indicated. The distance of centre of mass of the remaining portion from the centre of the original square plate is
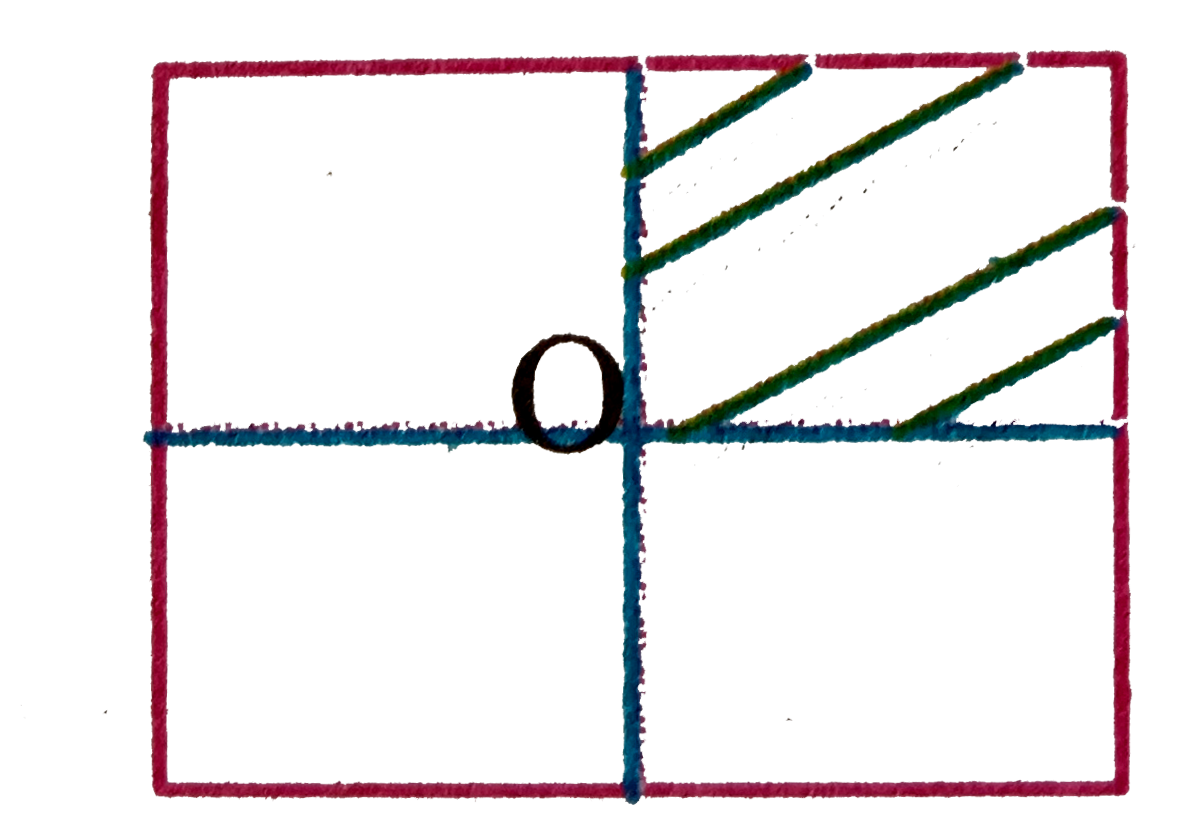 A1/3mB1/2mC1/6mD1/8m
A1/3mB1/2mC1/6mD1/8m
A circular plate of unifrom thickness has a diameter of 56cm. A circular portion of diameter 42cm is removed from the edge of the plate as shown in Fig. Find the position of centre of mass of the remaining portion.

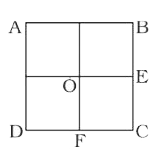
View SolutionA square of side 4m having uniform thickness is divided into four equal squares as shown in Fig. If one of the squares is cut off, find
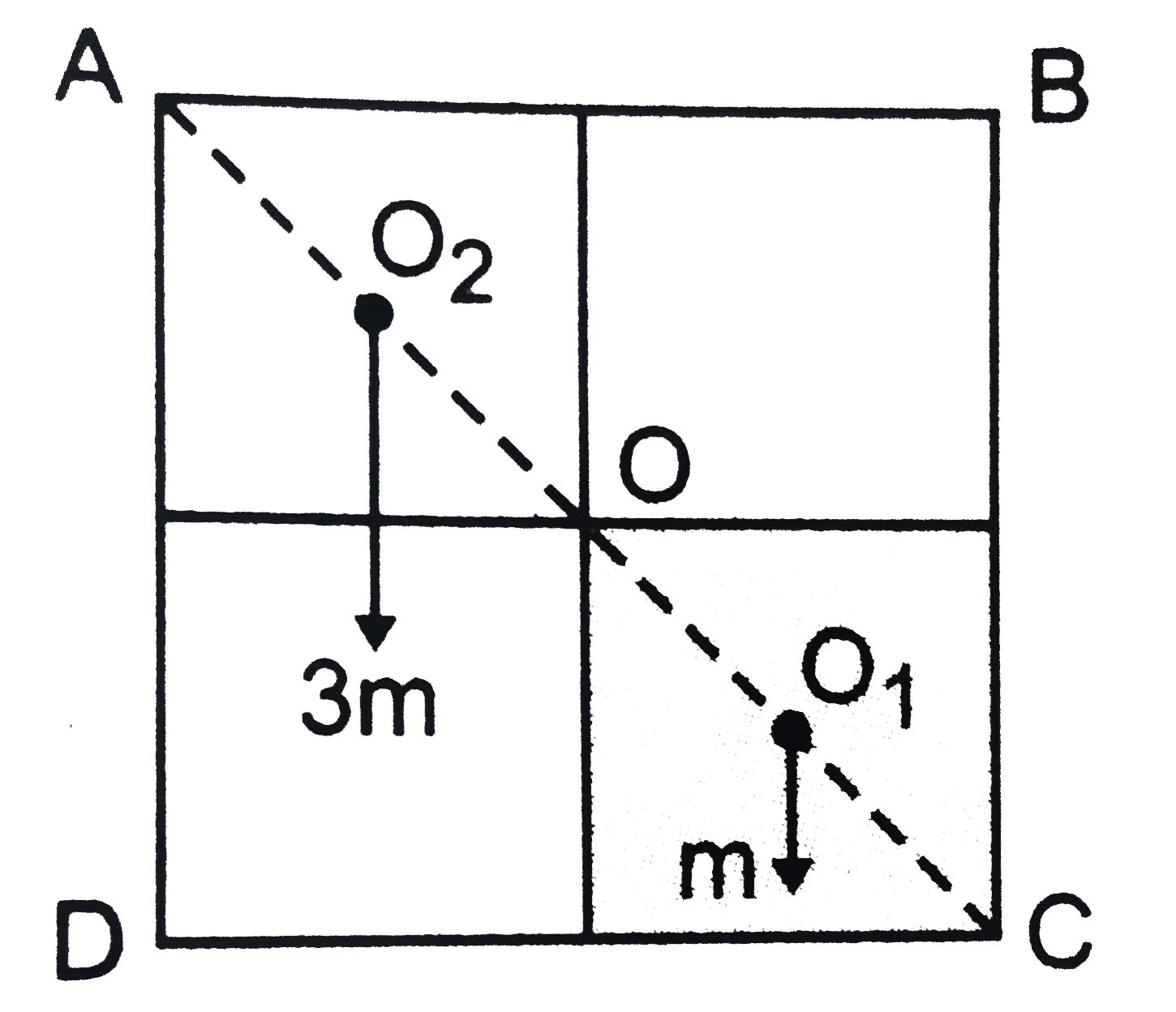
the position of centre of mass of the remaining portion from the centre O.
View SolutionA square of side 4 cm and of uniform thickness is divided into four equal squares. If one of them is cut off (OECF), then the position of the centre of mass of the remaining portion from O is √2kcm . Find the value of K.
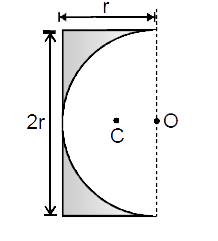
View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
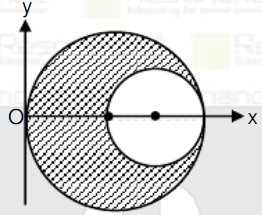
View SolutionA disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion
View SolutionFrom each of the two opposite corners of a square of side 8cm, a quadrant of a circle of radius 1.4 cm is cut. Another circle of diameter 4.2cm is also cut from the centre as shown in figure. Find the area of the remaining (shaded) portion of the square.
View Solution
